广度优先遍历

广度优先遍历

基础概念及图解

概念：

广度优先遍历算法是图的另一种基本遍历算法，其基本思想是尽最大程度辐射能够覆盖的节点，并对其进行访问。
以迷宫为例，广度优先搜索则可以想象成一组人一起朝不同的方向走迷宫，当出现新的未走过的路的时候，可以理解成一个人有分身术，继续从不同的方向走，，当相遇的时候则是合二为一

自我理解：

正如老师上课所说的，广度优先遍历就像在平静的湖面丢入一块石头，荡起的波纹，从离起始点最近的先开始遍历，同样距离的前后顺序可以交换，如果有环状结构，那遍历过的，就可以跳过，不用重复遍历。

例子解析

例子1：

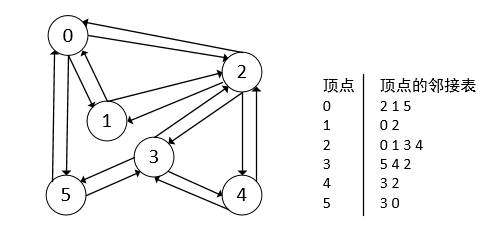
1.从起点0开始遍历

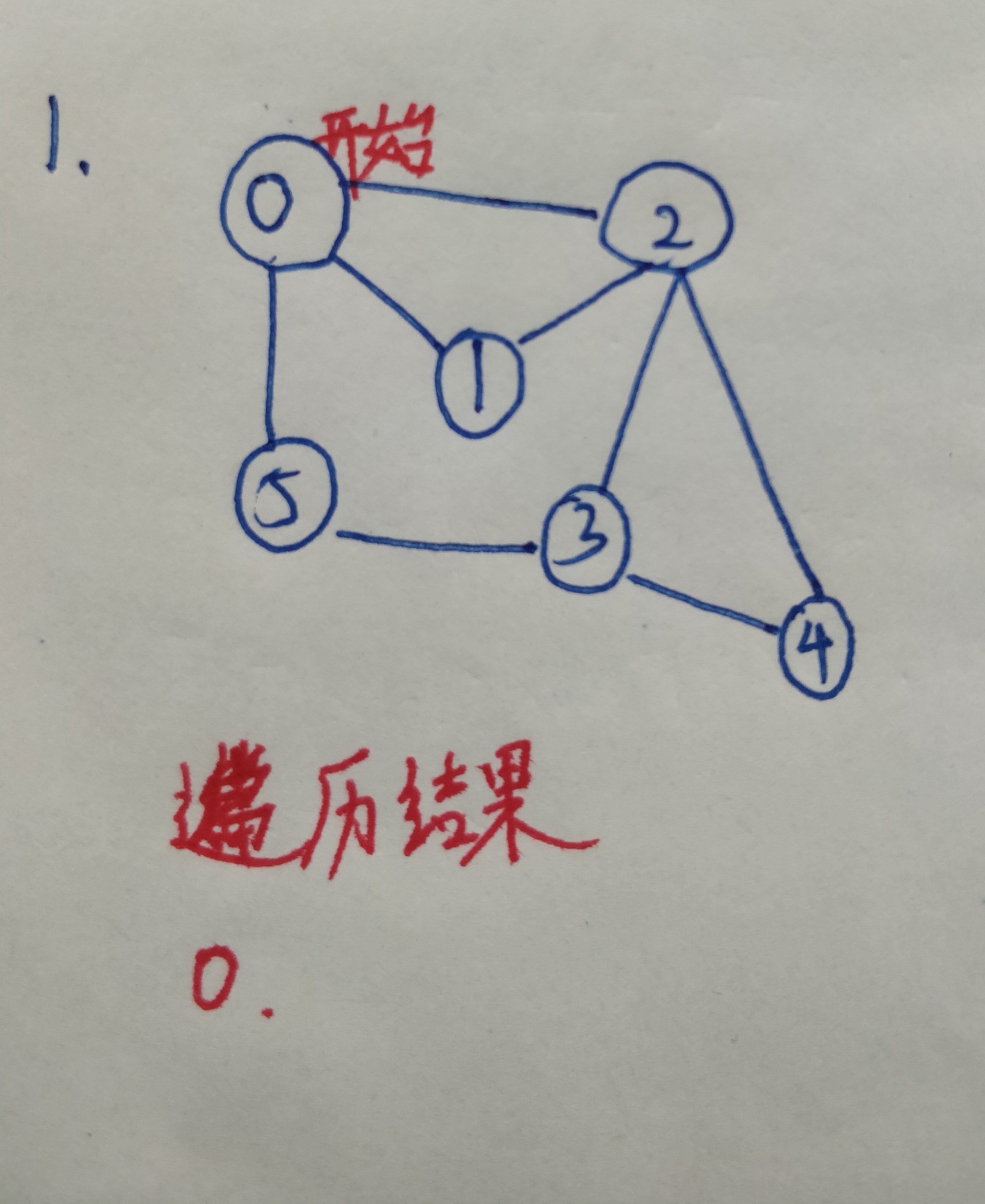
2.从其邻接表得到所有的邻接节点，把这三个节点都进行标记，表示已经访问过了

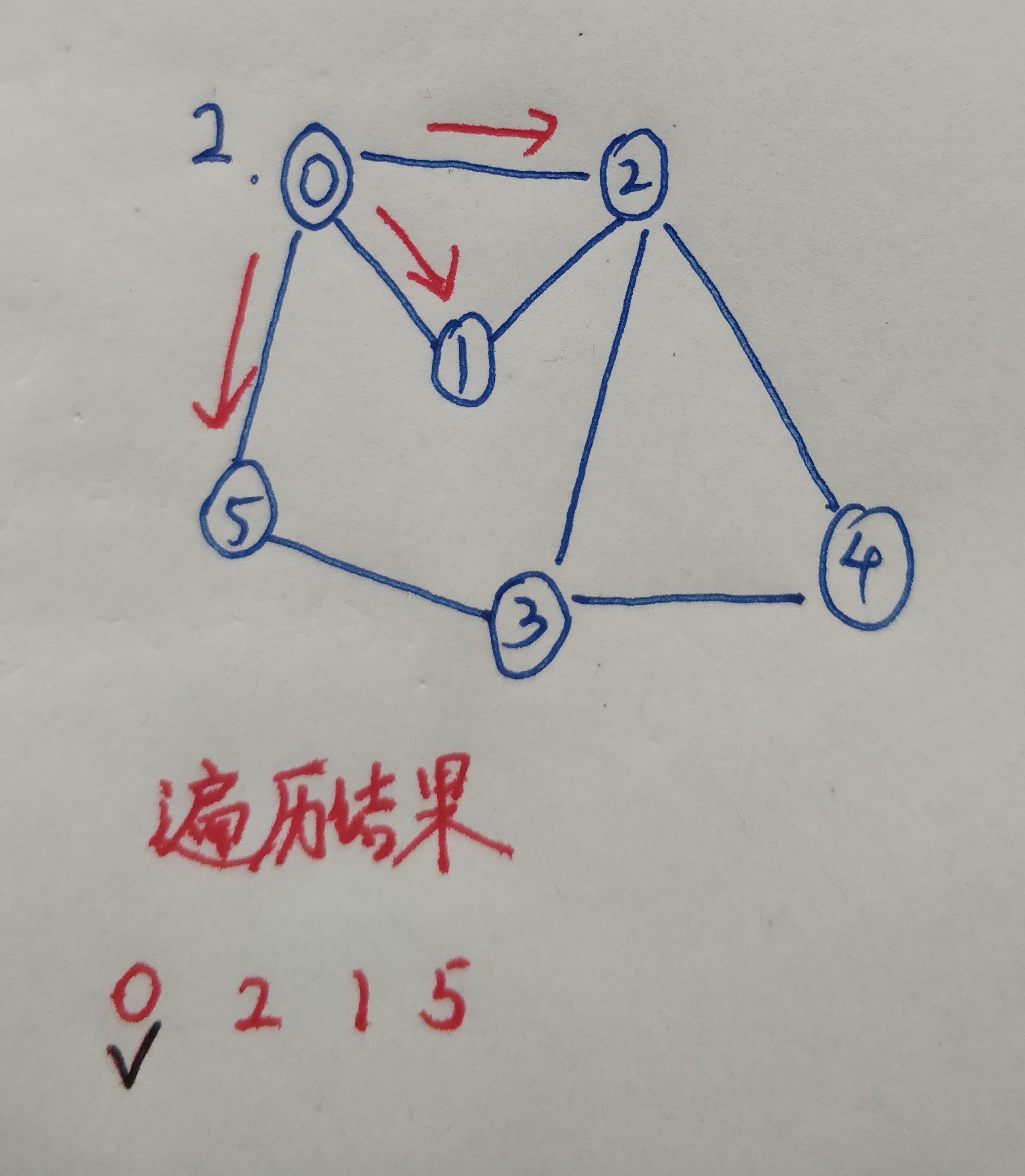
3.从0的邻接表的第一个顶点2开始寻找新的叉路

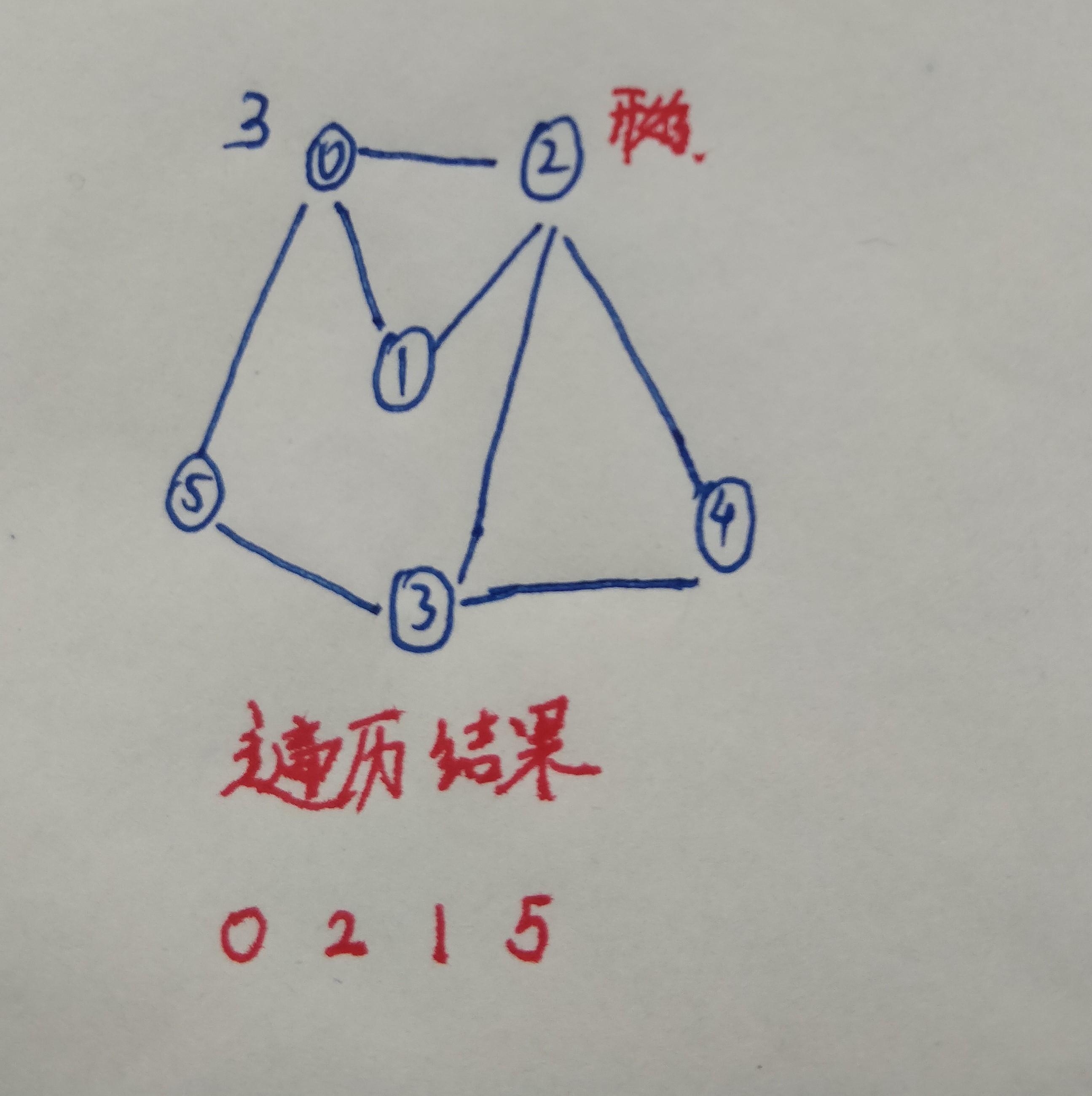
4.查询顶点2的邻接表，并将其所有的邻接节点都标记为已访问

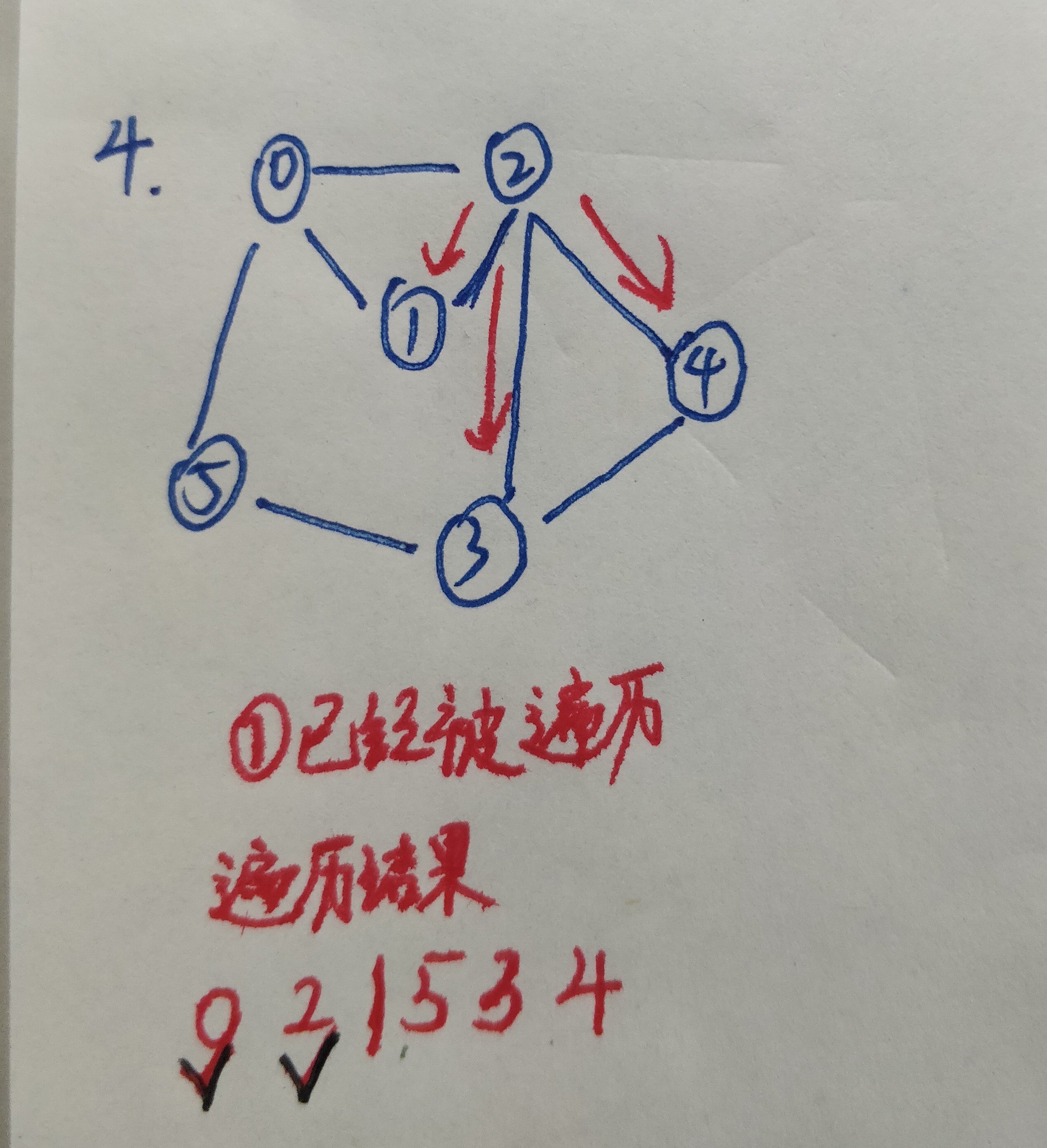
5.继续从顶点0的邻接表的第二个节点，也就是顶点1，遍历从顶点1开始

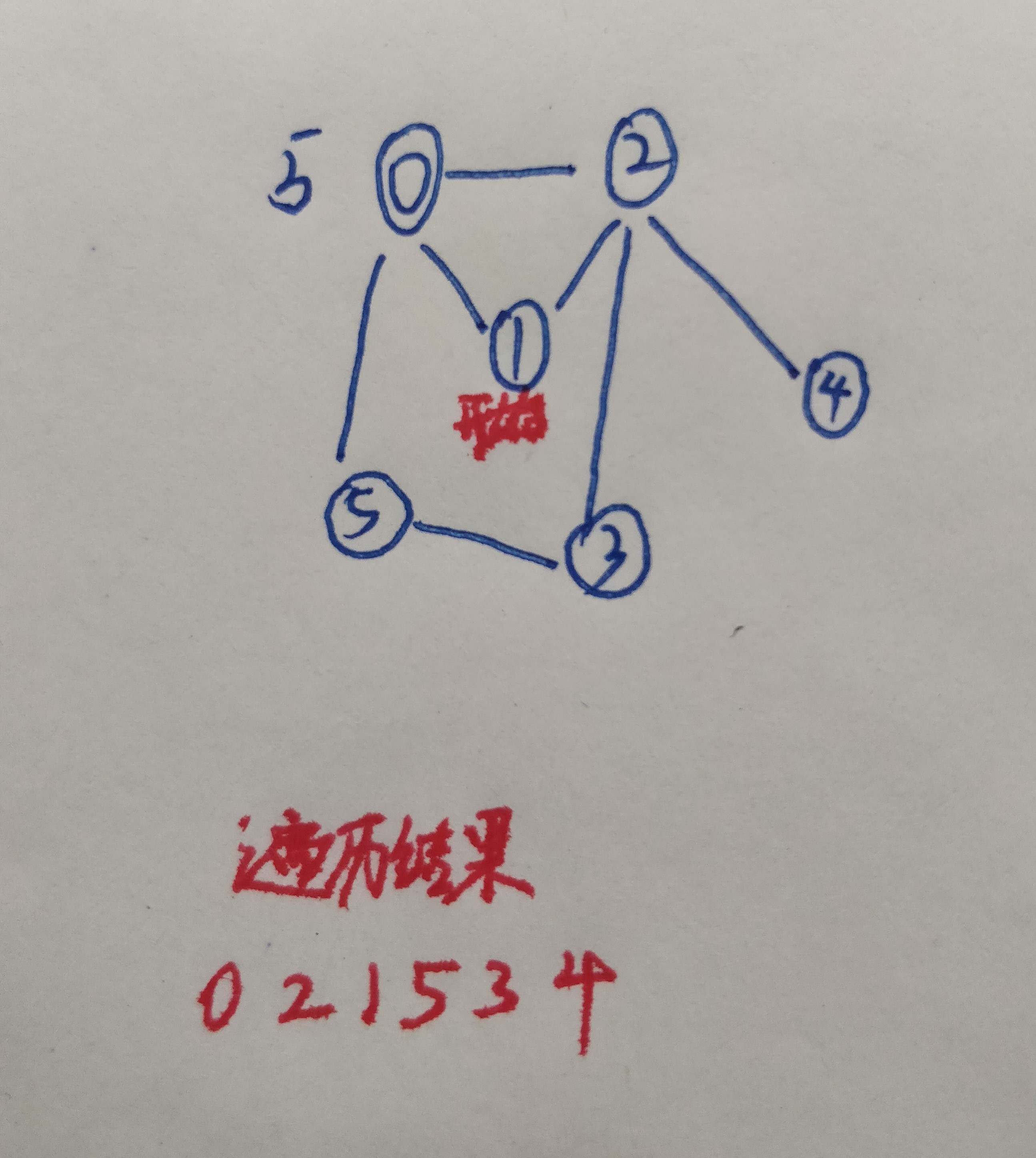
6.查询顶点1的邻接表的所有邻接节点，也就是顶点0和顶点2，发现这两个顶点都被访问过了，顶点1返回

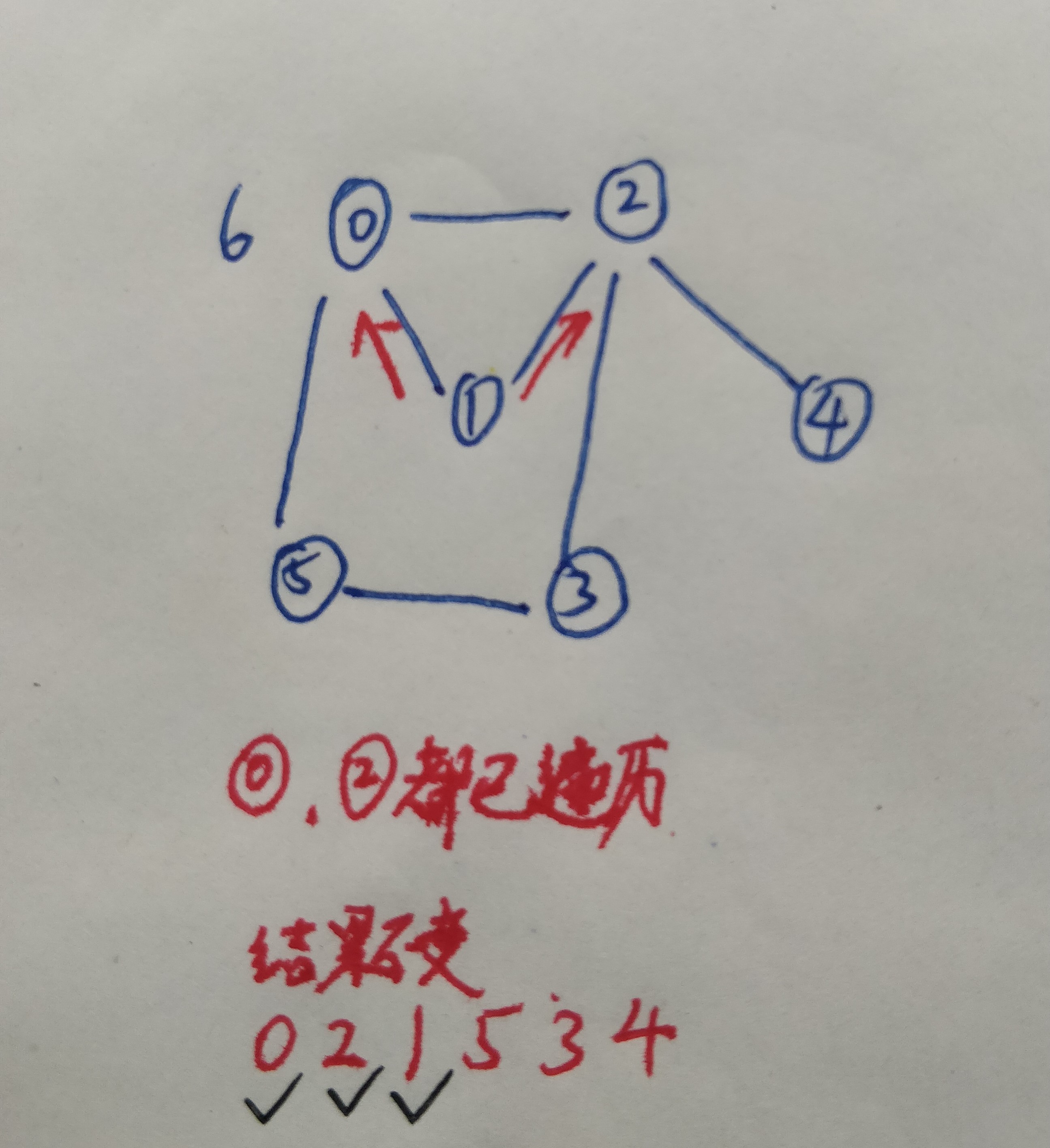
7.从顶点0的下一个邻接节点，也就是顶点5，开始遍历

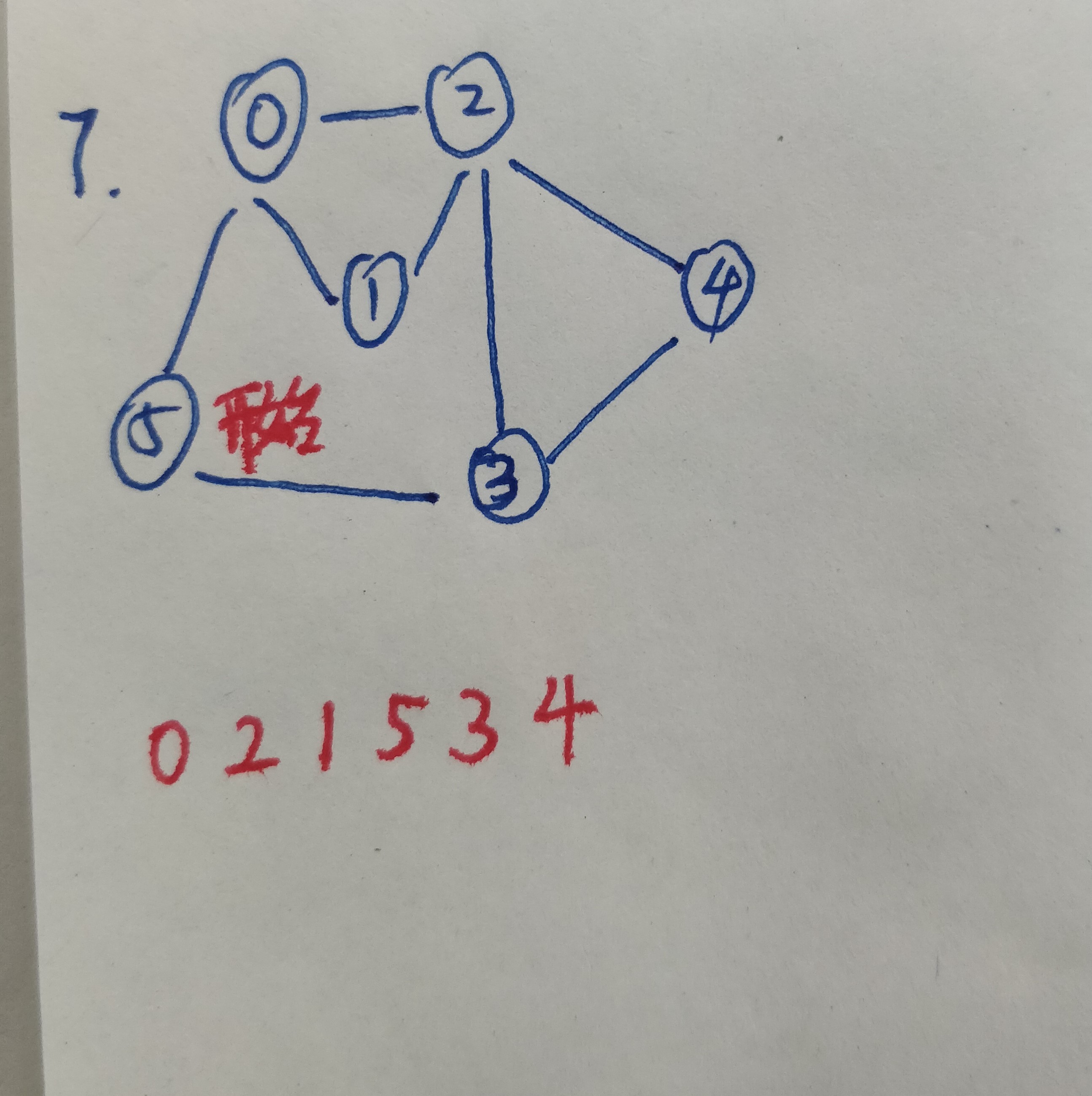
8.查询顶点5的邻接节点，发现其邻接节点3和0都被访问过了，顶点5返回

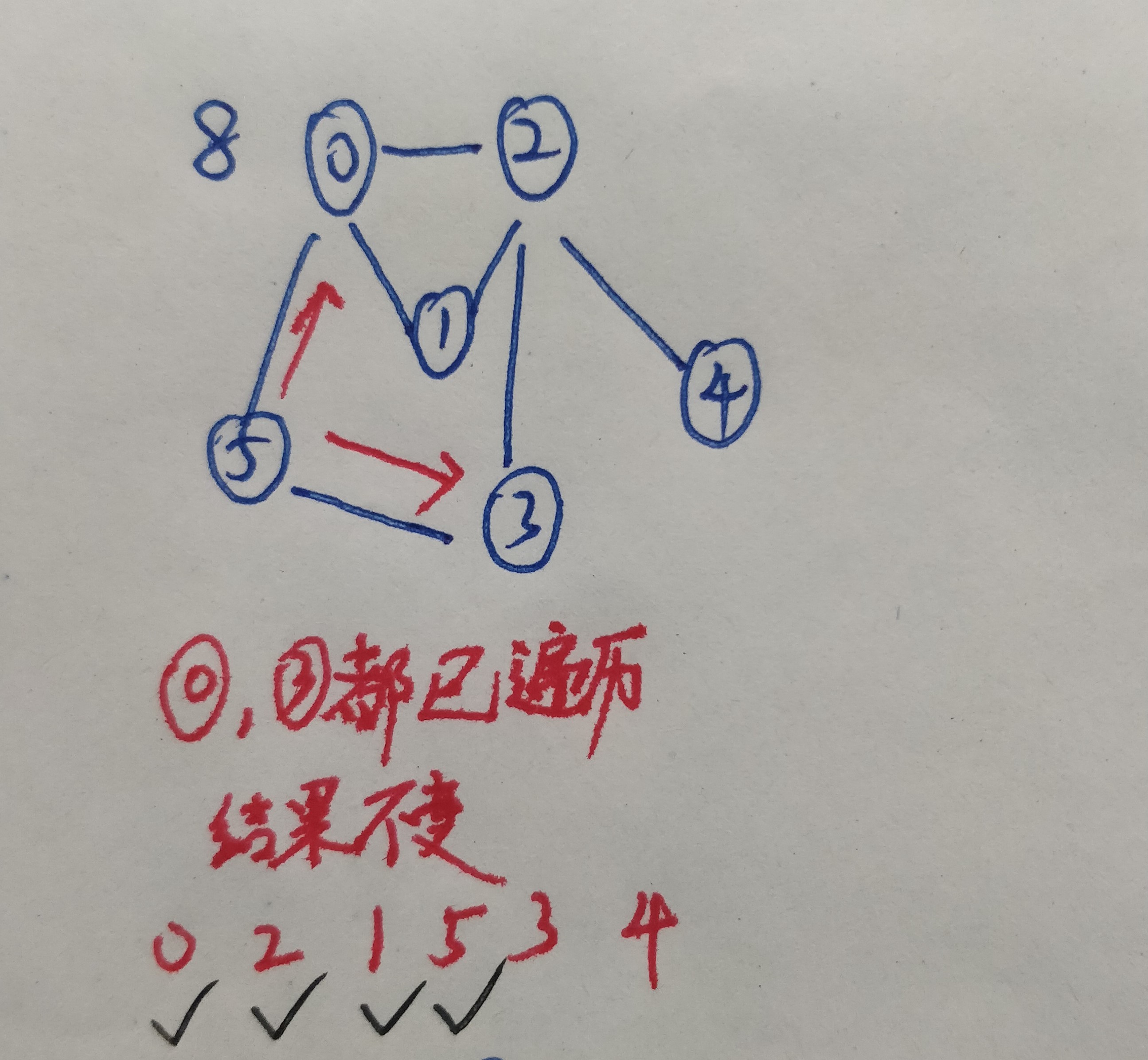
9.继续从2的下一个邻接节点3开始遍历

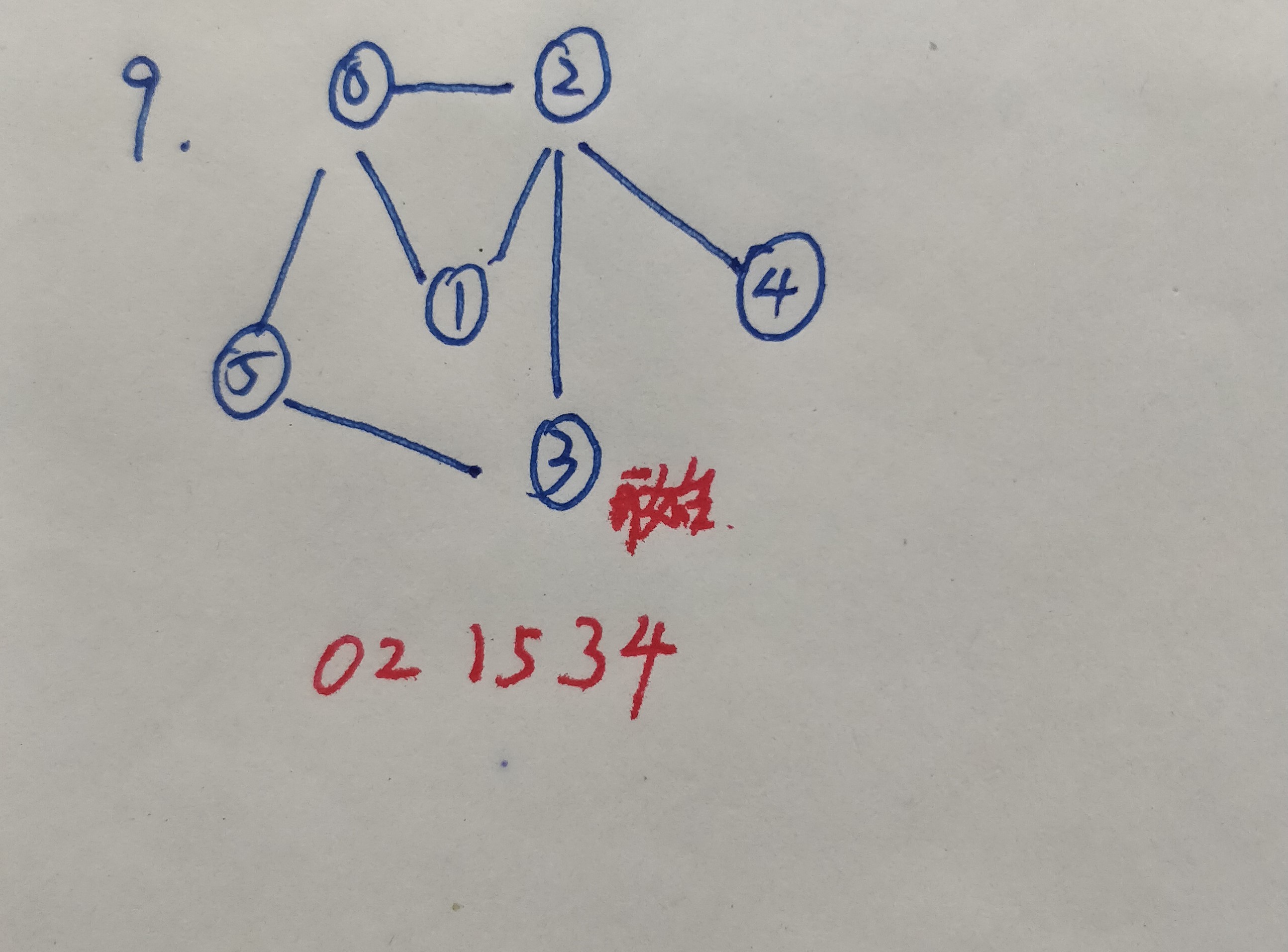
10.寻找顶点3的邻接节点，发现都被访问过了，顶点3返回

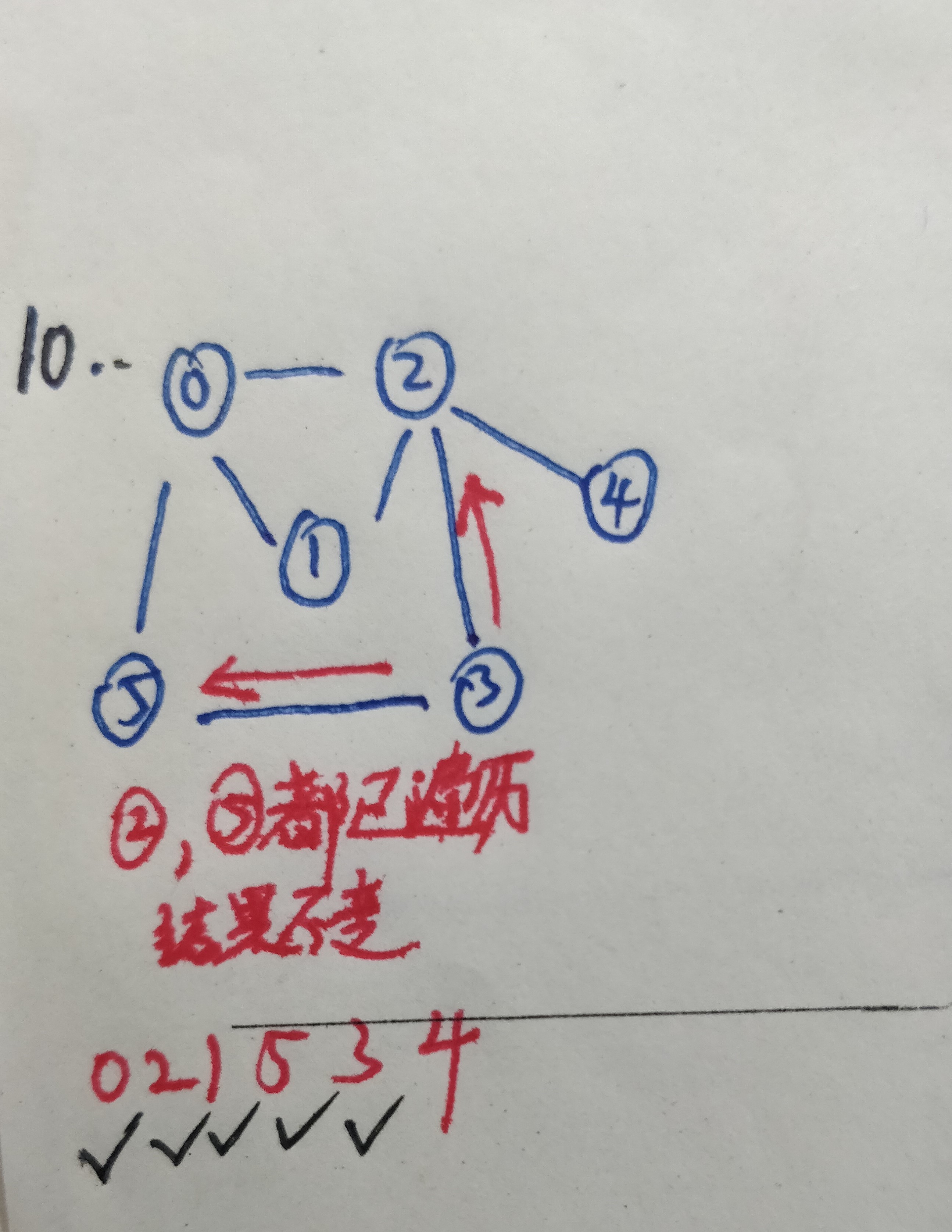
11.继续寻找顶点2的下一个邻接节点4，发现4的所有邻接节点都被访问过了，顶点4返回

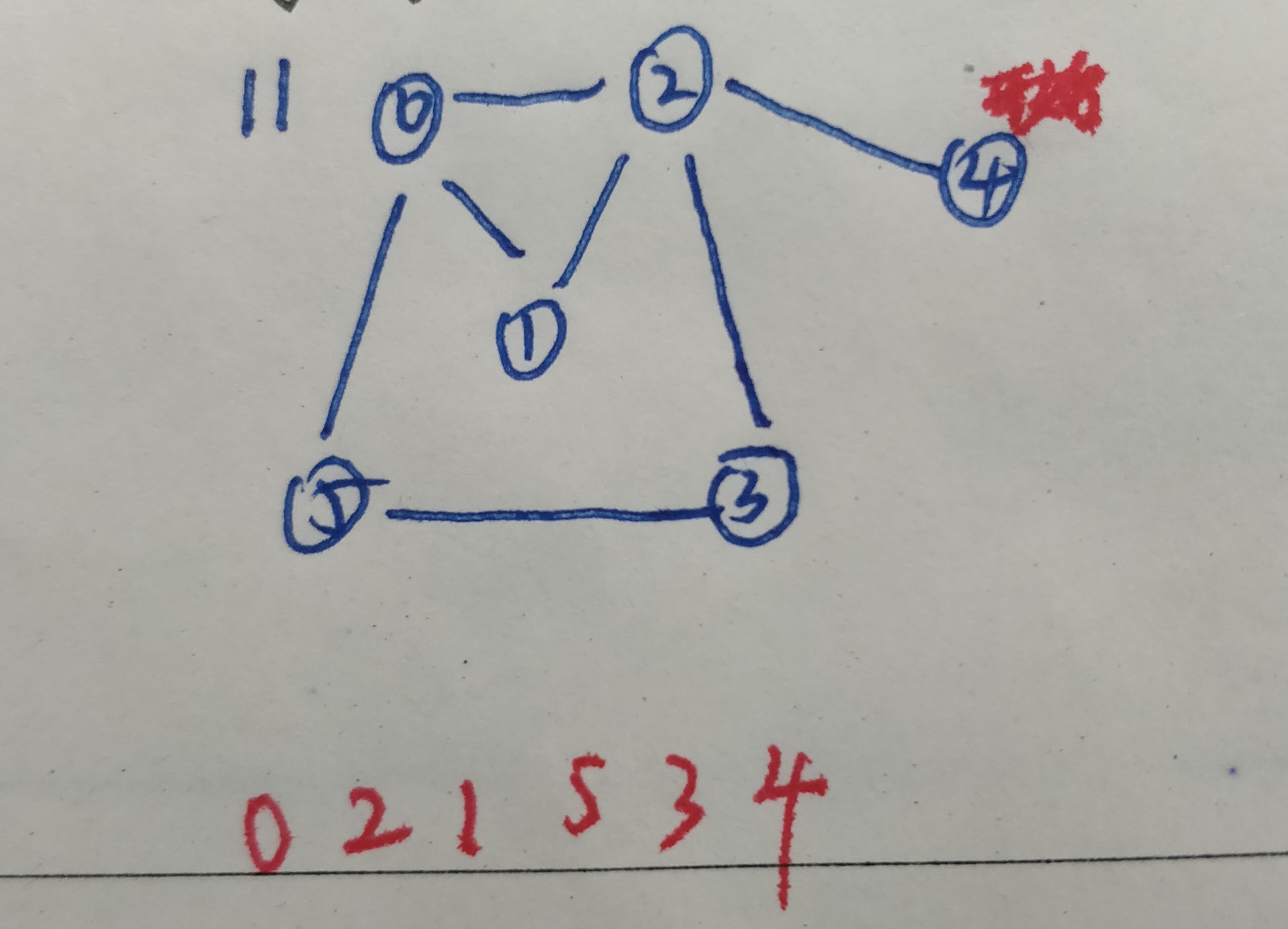
12.顶点2的所有邻接节点都放过了，顶点2返回，遍历结束

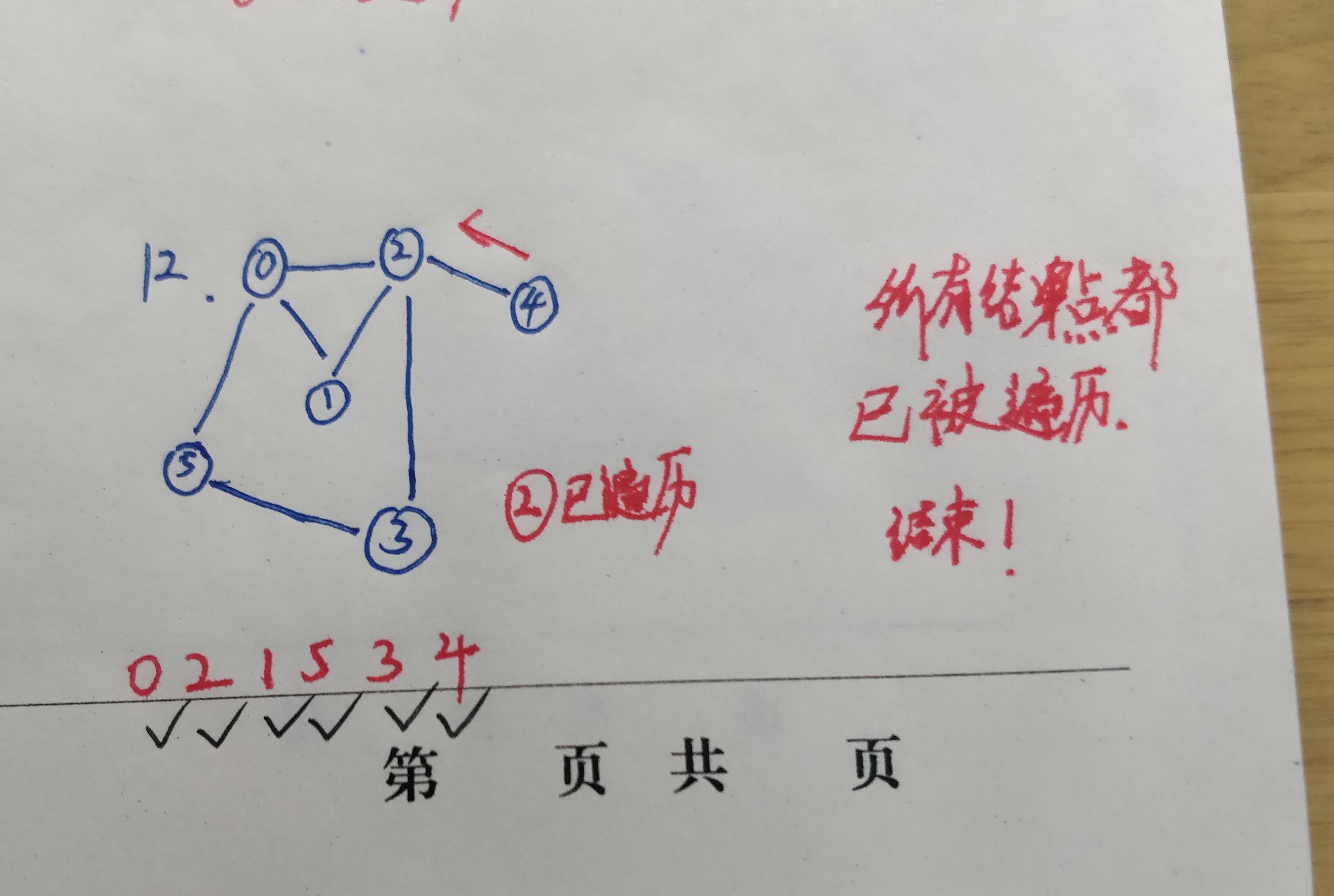
例子二

• 对下图连通无向图广度优先搜索（以v0为出发点）：v0,v1,v2,v3,v4,v5,v6,v7,v8
  

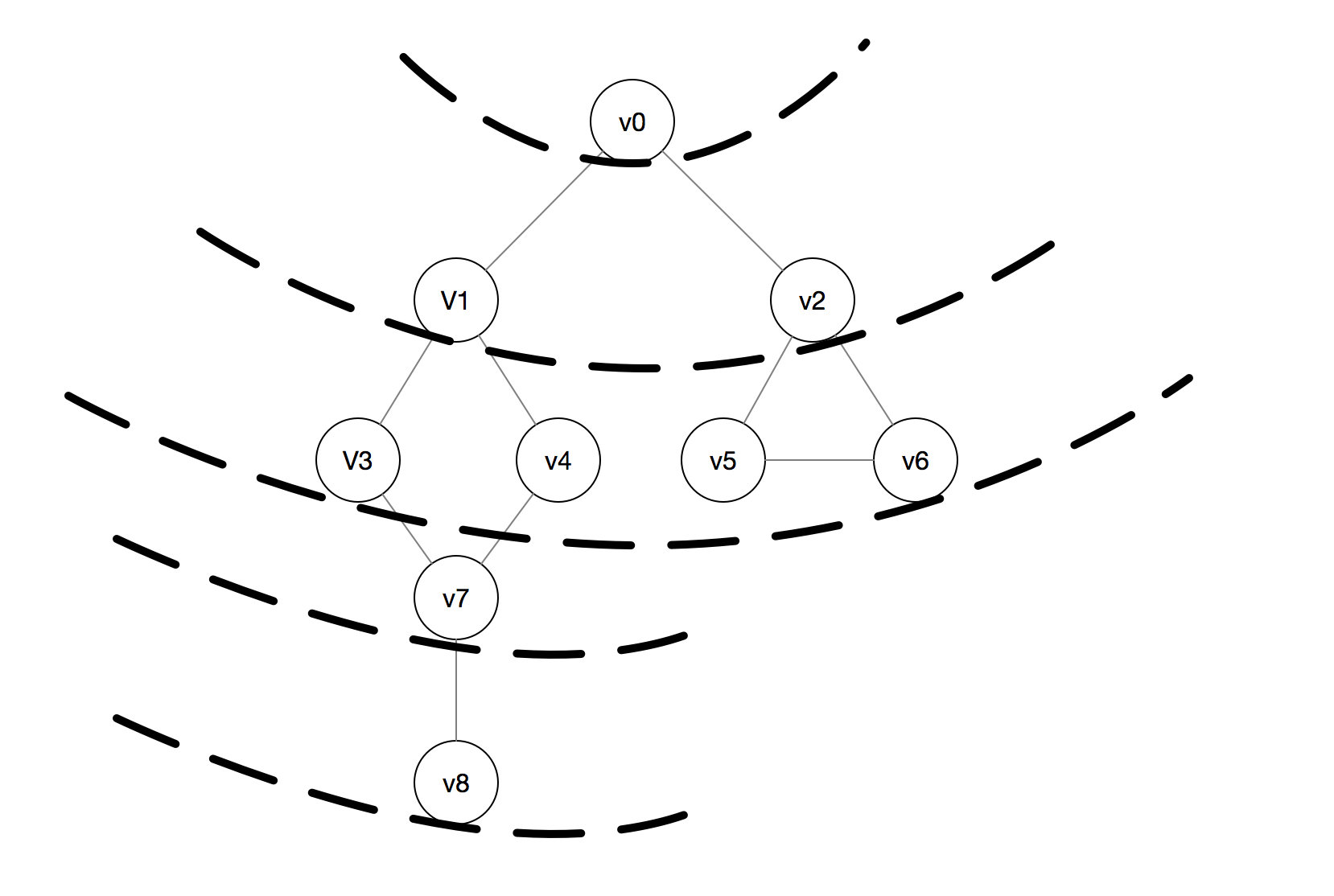
• 对下图非连通无向图广度优先搜索（以v0为出发点）：v0,v1,v2,v3,v4,v5,v6,v7，v4为另一个起始点
  
  

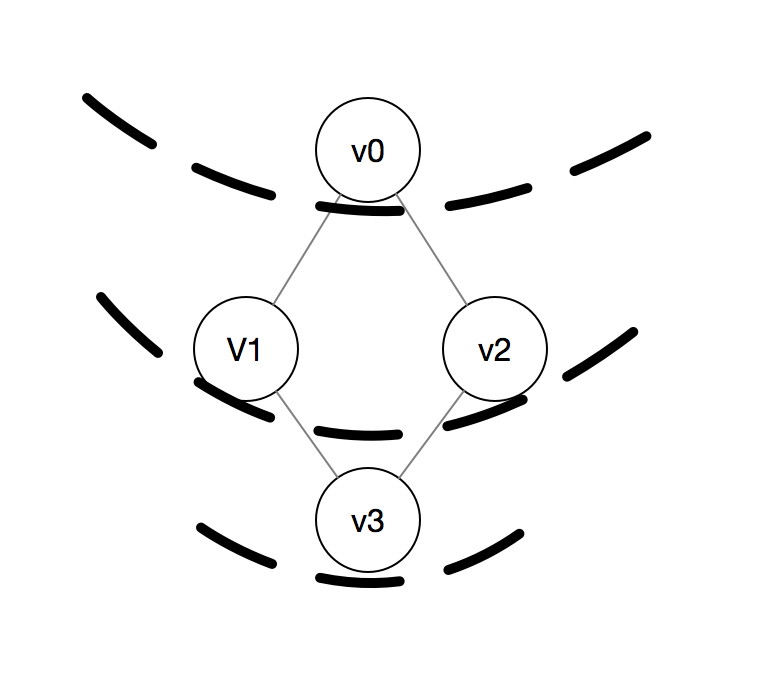
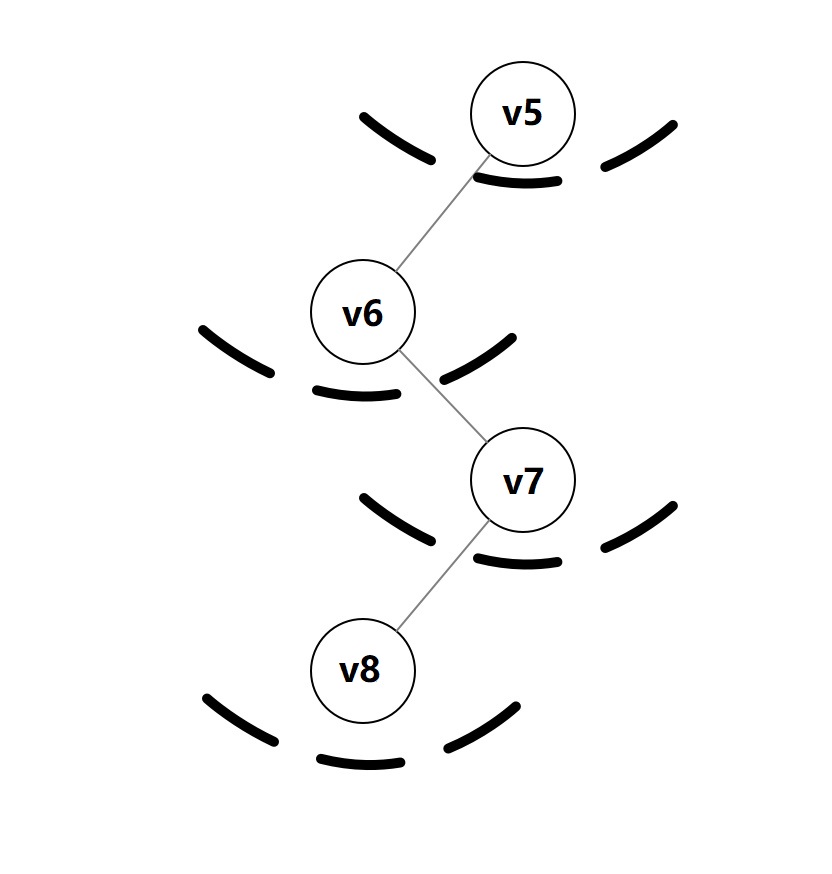
• 对下图有向图的广度优先搜索（v2为出发点）：v2,v1,v3,v0,v4
  

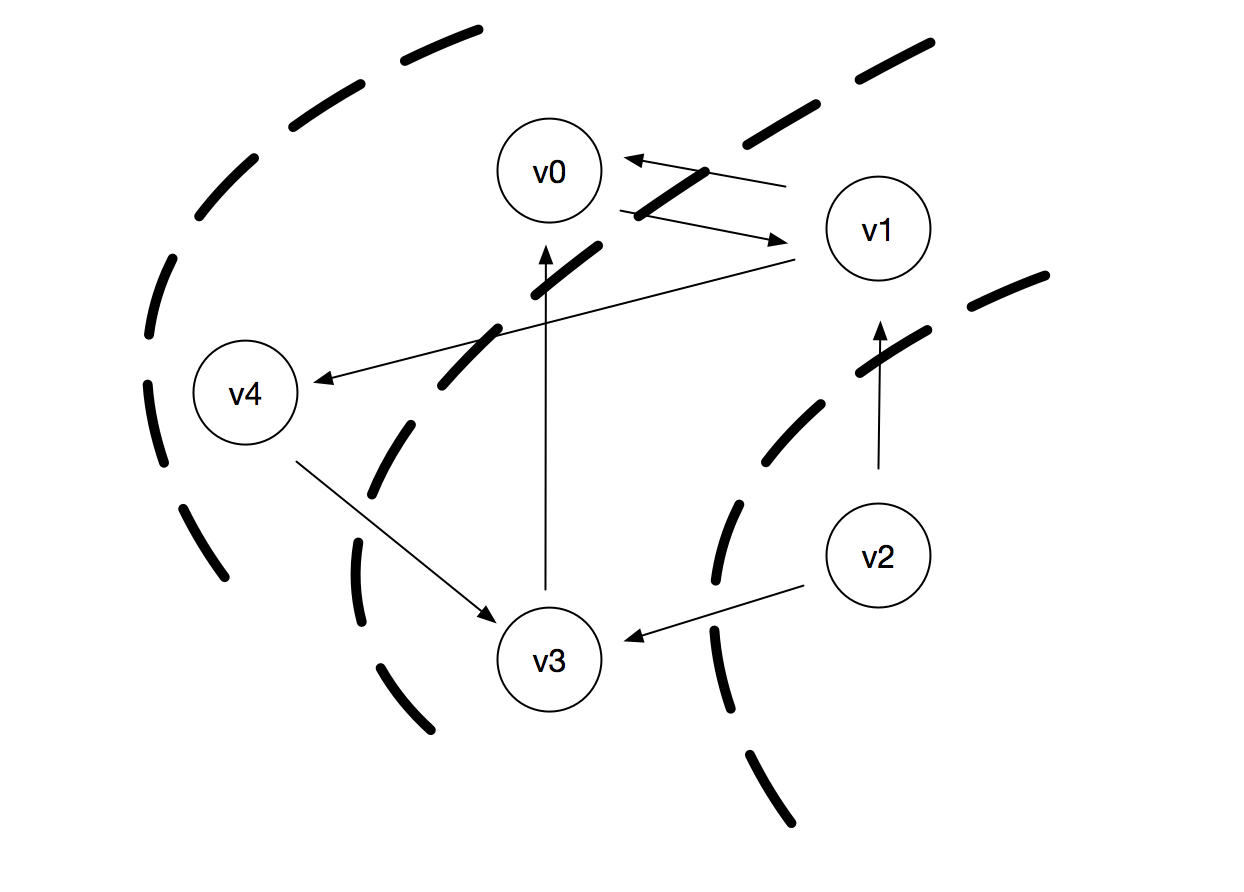
• 对下图有向图的广度优先搜索（v0为出发点）：v0,v1,v4,v3,v2，v2为另一出发点
  

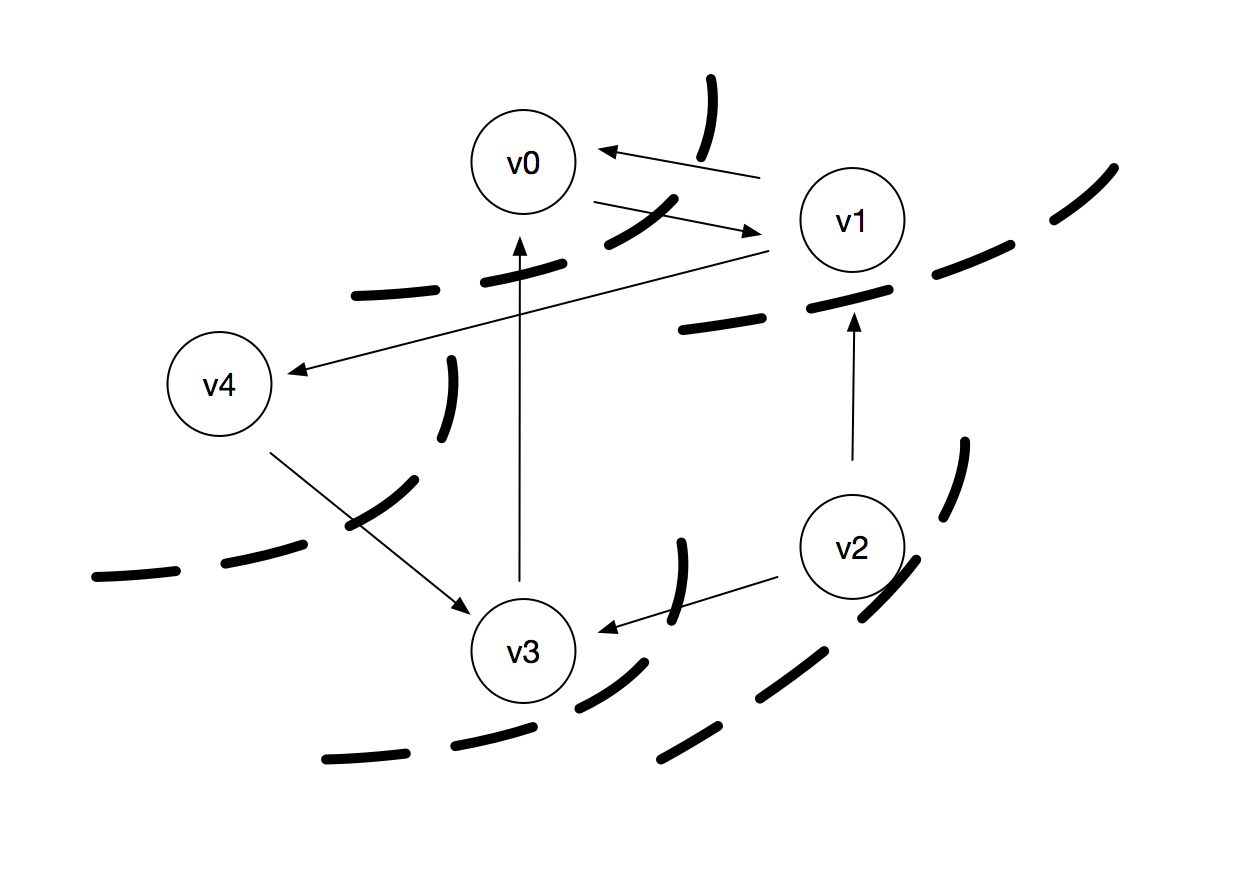
算法实现

private Iterator<T> iteratorBFS(int startIndex) {
    Integer x;//定义一个int型数字
    QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();//定义一个队列
    UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();//定义一个数组（该数组保存最后的遍历后顺序）
    //索引无效，返回空。即如果索引值不在数组索引值范围内，返回空。
    if (!indexIsValid(startIndex))
        return resultList.iterator();
    boolean[] visited = new boolean[maxCount];//新建一个Boolean型数组，大小和上面数组一样
    //把所有顶点设为false，白色
    for (int i = 0; i < maxCount; i++)
        visited[i] = false;
    //进入队列的为true，即访问过的，灰色
    traversalQueue.enqueue(startIndex);//先将起始结点加入队列中
    visited[startIndex] = true;//并将该结点在Boolean型数组中由false改为ture，表示已经被遍历过。
    while (!traversalQueue.isEmpty()) //如果队列不为空
       {        
       //出队列涂黑存入resultList中
        x = traversalQueue.dequeue();//将队列里的数取出
        resultList.addToRear((T) nodelist.get(x).getElement());//并将其存入数组里
        //如果进入resultList的顶点还有相邻的未访问过的顶点，将其涂灰入队
        for (int i = 0; i < maxCount; i++) 
            {
            if (hasEdge(x, i) && !visited[i]) //如果进入resultList的顶点还有相邻的未访问过的顶点
                {                
                traversalQueue.enqueue(i);//将其加入队列
                visited[i] = true;//标为已经遍历过
                Int++;
                }
            }
         }
    return new GraphIterator(resultList.iterator());
    }