动态规划小例子

Description：

The rod-cutting problem is the following. Given a rod of length n inches and a table of prices p_i for i D 1，2，…，n, determine the maximum revenue rn obtainable by cutting up the rod and selling the pieces. Note that if the price pn for a rod of length n is large enough, an optimal solution may require no cutting at all.

以下给出的样例：

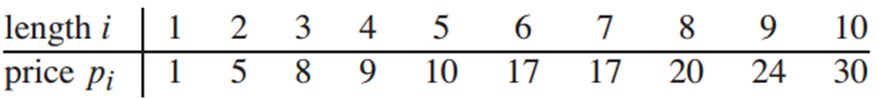
Analysis：

长度为n的钢条可以有2^n-1中切割方案，所以当n很大时用暴力求解的方法是行不通的。假设将该钢条切割成k(k的取值为[1,n])段，切割顺序为从钢条的左端开始，那么最有切割方案是：

n = len₁+len₂+len₃+…+len_k

将钢条切割为长度是len1，len2，…，lenk的小段，得到最大收益

r_n = p _len1+p _len2+p _len3+…+p _lenk

根据样例给出的价格表，可以得到最大收益值ri（i=1,2,…,10）及对应的切割方案。

i	最大收益	切割方案
1	1	无切割
2	5	无切割
3	8	无切割
4	10	4 = 2 + 2
5	13	5 = 2 + 3
6	17	无切割
7	18	7 = 1 + 6 或7 = 2 + 2 + 3
8	22	8 = 2 + 6
9	25	9 = 3 + 6
10	30	无切割

由上表可以得出：长度为n的钢条其最大收益值和长度为k和n-k的两条钢条的最大收益值相关。

我们可以假设长度为n的钢条的最大收益值：

r_n = max(p_n,r₁+r_n-1,r₂+r_n-2,…,r_n-1+r₁)，p_n为不切割时的价格。

这样可以通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解。

另一种思路：将钢条从左边切割长度为i的一段，只对右边剩下的长度为n-i的一段继续进行切割(递归求解)，对左边的一段则不再进行分割。

r_n = max(p_i + r_n-i) (i取值范围[1,n])

在这个公式中，原问题的最优解只包含一个相关子问题(右端剩余部分)的解。

自顶向下的递归算法实现

 1 //自顶向下递归实现，prof[]是样例给出的价格表
 2 int cutRod(int prof[], int n)
 3 {
 4     if (n == 0)
 5         return 0;
 6     else
 7     {
 8         int profit = 0;
 9         for (int i = 1; i <= n; i++)
10             profit = max(profit, prof[i] + cutRod(prof, n - i));
11         return profit;
12     }
13 
14 }

根据代码可以分析得出：

随着n的增大，程序的运行时间会成倍的增加。原因是，cutRod反复地用相同的参数值对自身进行递归调用，即它反复求解相同的子问题。

当 n = 4时，递归调用树如下：

 

 

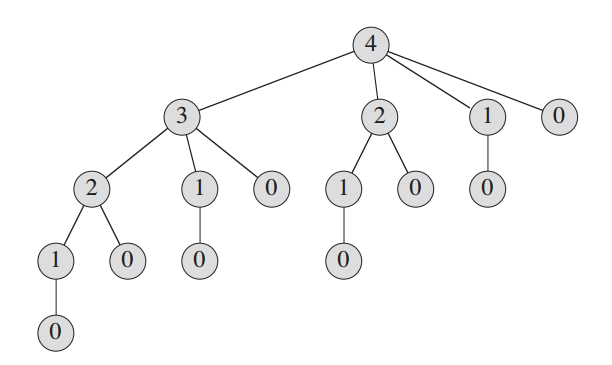
cutRod的运行时间为n的指数函数，T(n)= 2ⁿ

使用动态规划方法求解钢条切割的最优化问题

1、带备忘的自顶向下法

备忘就是一张存储每次计算最佳收益的表，这样就可以避免“自顶向下递归算法”中出现的重复计算重叠子问题的情况。

int memoizedCutRodAux(int pro[], int r[], int n)
{
    if (r[n] > 0)
        return r[n];
    else
    {
        int profit = 0;
        for (int i = 1; i <= n; i++)
            profit = max(profit, pro[i] + memoizedCutRodAux(pro, r, n - i));
        r[n] = profit;
        return profit;
    }
}

2、自底向上法

int bottomUpCutRod(int pro[], int r[], int n)
{
    for (int i = 1; i <= n; i++)
    {
        int profit = 0;
        for (int j = 1; j <= i; j++)
            profit = max(profit, pro[j] + r[i - j]);
        r[i] = profit;
    }
    return r[n];
}

现在把思路一中r_n = max(p_n,r₁+r_n-1,r₂+r_n-2,…,r_n-1+r₁)的算法给出

int bottomUpCutRodTwo(int pro[], int r[], int n)
{
    for (int i = 1; i <= n; i++)
    {
        int profit = pro[i];
        for (int j = 1; j <= i / 2; j++)
            profit = max(profit, r[j] + r[i - j]);
        r[i] = profit;
    }
    return r[n];
}

对第二个for循环中j <= i / 2;解释一下，从等式r_n = max(p_n,r₁+r_n-1,r₂+r_n-2,…,r_n-1+r₁)，可以看出,r₁+r_n-1和r_n-1+r₁其实是一样的。所以没有必要循环到i,截至到i/2即可。

钢条切割问题的子问题图

 

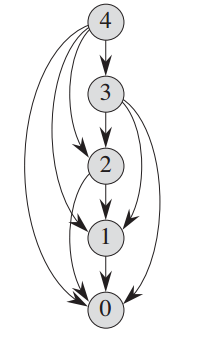
可以看出该图是一个有向图，每个顶点唯一地对应一个子问题，若是求子问题x的最优解时需要直接用到其子问题y的最优解，那么在子问题图中就会有一条从子问题x的顶点到子问题y的顶点的有向边。子问题G=(V,E)的规模可以确定动态规划的运行时间，由于每个子问题只求解一次，因此算法的运行时间等于每个子问题求解时间之和。通常，一个子问题的求解时间与子问题图中对应顶点的出度成正比，而子问题的数目等于子问题图中顶点数。因此，通常情况下，动态规划的运行时间与顶点和边的数量呈线性关系。

总结：结合动态规划的算法设计步骤来说，钢条切割问题也是遵守其标准的。

第一步先确定最优化解的结构特征：最优切割方案是由第一次切割后得到的两段钢条的最优切割方案组成的，或者是第一次切割后，其右端剩余部分的最优切割方案组成的。

第二步递归定义最优解的值，由上面的分析我们可以得到r_n = max(p_n,r₁+r_n-1,r₂+r_n-2,…,r_n-1+r₁)和r_n = max(p_i + r_n-i) 两个最优解的公式，其满足求得原问题最优解的条件。

第三步根据得到的求最优解公式，计算出结果。我们用到了两种方法：带备忘的自顶向下递归法和自底向上法（非递归）。

第四步构造出最优解。