前缀和
前缀和是一种重要的预处理,能大大降低查询的时间复杂度。
最简单的一道题就是给定 n 个数和 m 次询问,每次询问一段区间的和。求一个 O(n + m) 的做法。
用 O(n) 前缀和预处理,O(m) 询问。
主要代码
1 for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + a[i]; //O(n) 2 while(m--) //O(m) 3 { 4 int L, R; scanf("%d%d", &L, &R); 5 printf("%d\n", sum[R] - sum[L - 1]); 6 }
升级版
给定一个n*n的矩阵,找一个最大的子矩阵,使得这个子矩阵里面的元素和最大。
这道题最朴素的算法是 O(n ^ 6),用二维前缀和可以降到 O(n ^ 4)。
再想想前缀和矩阵怎么生成?看个图就明白了:

那么最大的矩形前缀和就等于蓝的矩阵加上绿的矩阵,再减去重叠面积,最后加上小方块,即
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j]
主要代码
1 for(int i = 1; i <= n; ++i) 2 for(int j = 1; j <= n; ++j) 3 sum[i][j] = sum[i - 1][j] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j]; 4 for(int i = 1; i <= n; ++i) //枚举矩阵左右端点 5 for(int j= 1; j <= n; ++j) 6 for(int k = i; K <= n; ++k) 7 for(int h = j; h <= n; ++h) 8 { 9 tot = sum[k][h] - sum[i - 1][h] - sum[k][j - 1] + sum[i - 1][j - 1]; //同理矩阵生成 10 ans = max(ans, tot); 11 }
不过这道题还有另一种方法,可达到 O(n ^ 3),不过思路就和二维前缀和有些差别了。
为了更好理解,先降维做道题。
给定一个数字序列,求最大区间和。
其实这道题使用贪心的思想。因为 sum[L, R] = sum[R] - sum[L - 1],所以只要在枚举 R 的同时,一直取最小的 sum[L - 1],然后尝试着更新 ans。
这个代码实现有很多种方法,以下给出两种,都很好理解
第一种
1 for(int R = 1; R <= n; ++R) //已知s[R],找最小的s[L-1] 2 { 3 MIN = min(MIN, s[R - 1]); //就是求 sum[L] 4 ans = max(ans, s[R] - MIN); 5 }
第二种
1 for(int i = 1; i <= n; ++i) 2 { 3 sum += a[i]; 4 if (sum < 0) sum = 0; //若小于0,就重新计数 5 ans = max(ans, sum); 6 }
掌握了这两种方法,就可以解矩阵这道题了
只要枚举矩阵的上下边。
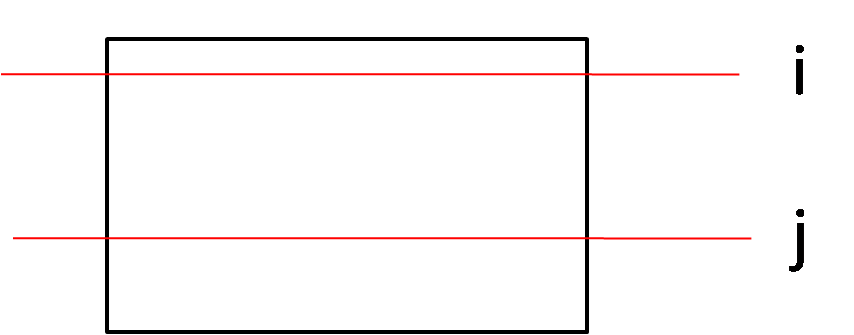
这里面的矩阵就可以延 i 到 j 的方向将维,再用上述思想更新答案
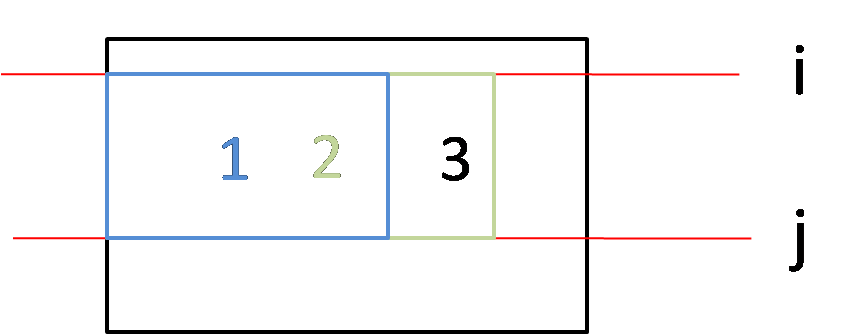
矩阵2减去矩阵1就得到矩阵3,然后将矩阵3降维。
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 const int maxn = 4e2 + 5; 8 const int INF = 0x3f3f3f3f; 9 int n, ans = -INF; 10 int a[maxn][maxn], f[maxn][maxn]; //f[i][j]关于第j列到第i行的列前缀和 11 void init(const int& n) 12 { 13 for(int i = 1; i <= n; ++i) 14 for(int j = 1; j <= n; ++j) 15 f[i][j] = f[i - 1][j] + a[i][j]; //求一列的和 16 } 17 int b[maxn], sum[maxn]; //降维后的数组 18 int main() 19 { 20 scanf("%d", &n); 21 for(int i = 1; i <= n; ++i) 22 for(int j = 1; j <= n; ++j) 23 scanf("%d", &a[i][j]); 24 init(n); 25 for(int i = 1; i <= n; ++i) 26 for(int j = i; j <= n; ++j) 27 { 28 for(int k = 1; k <= n; ++k) b[k] = f[j][k] - f[i - 1][k]; //降维 29 for(int k = 1; k <= n; ++k) sum[k] = sum[k - 1] + b[k]; //求一维前缀和 30 int Min = INF; 31 for(int k = 1; k <= n; ++k) 32 { 33 Min = min(Min, sum[k - 1]); 34 ans = max(ans, sum[k] - Min); 35 } 36 } 37 printf("%d\n", ans); 38 return 0; 39 }
总而言之,前缀和虽然大多数用来预处理,但要是出关于它的题也能出的很难。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号