线段树初步
还是先来一道题,方便理解线段树的特性(因为我实在想不出来啥方法了)
题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
输出样例
14 16
en。。。若是求一个静态数列中的每个数的和的话,倒是可以用前缀和或是分块的思想来求,然而题目还要求改变某一个数的值,若用前缀和的话,那就得再重新算一遍,实在麻烦,而且这不就跟暴力没什么区别了嘛。所以,为了解决这种动态区间的求和问题,我们 OI 界的前辈们就发明了一种很牛的数据结构——线段树。
当然,线段树能解决的问题可远不止这些。
那么什么是线段树呢?简单来说,线段树就是利用分治的思想,将区间不断一分为二,直到每一个区间只有一个元素为止,是一种二叉树,但不一定是完全二叉树(很容易想出来)。
那么若数列长度为 n ,则树共有 logn 层,时间复杂度为 O(nlogn)。
上一个图或许更直观些?
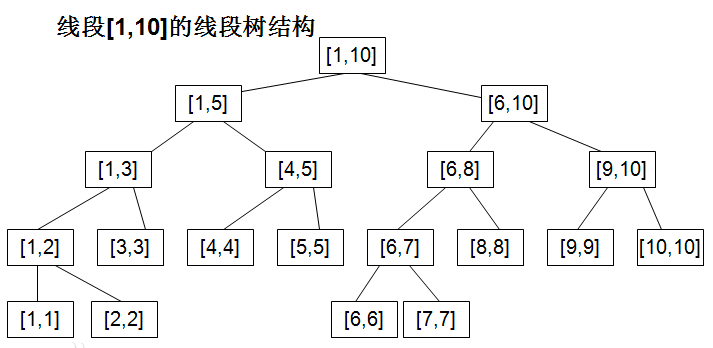
为了方便,我们按照从上到下、从左到右的顺序给所有结点编号为1,2,3,,......,则编号为 i 的结点,它的左右子结点编号为 2 * i 和 2 * i + 1。
线段树算法一般有这么几个操作:建树(build)、更新(update)、询问(query)。都可以递归完成。
就拿这道题为例,先是建树。
build 函数中一般有控制区间左右端点的两个变量和当前的结点编号。
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 typedef long long ll; 8 const int maxn = 5e5 + 5; 9 int l[4 * maxn], r[4 * maxn]; 10 ll sum[4 * maxn]; 11 void build(int L, int R, int now) 12 { 13 l[now] = L; r[now] = R; 14 if(L == R) 15 { 16 /* 递归边界:左右端点重合,说明此时区间里只有一个元 17 素,正好就可以读入数据,而且此时读入的也正好是该区间 18 的区间和 */ 19 scanf("%lld", &sum[now]); return; 20 } 21 int mid = (L + R) >> 1; 22 build(L, mid, now << 1); //构建左子树 23 build(mid + 1, R, now << 1 | 1);//构建右子树,注意从 mid + 1开始 24 sum[now] = sum[now << 1] + sum[now << 1 | 1]; 25 // 该区间和就等于左右子区间和的加和 26 }
挺好理解。
然后是更新。对于这道题,更新还是挺简单的。(毕竟是板子题嘛)
1 void update(int idx, int d, int now){ 2 //idx 代表结点编号,d 代表这个数加上 d 3 sum[now] += d; 4 if (l[now] == r[now]) return; //到达叶结点了 5 int mid = (l[now] + r[now]) >> 1; 6 //然后判断要更新的点在左还是右子树中 7 if (idx <= mid) update(idx, d, now << 1); 8 else update(idx, d, now << 1 | 1); 9 }
最后是查询,就是对于给定的区间,判断它在左子树还是右子树中,或是两者兼得。再在子树中递归寻找,直到找到的区间刚好和给定的区间吻合。
1 ll query(int L, int R, int now){ 2 if (L == l[now] && R == r[now]) return sum[now]; 3 int mid = (l[now] + r[now]) >> 1; 4 if (R <= mid) return query(L, R, now << 1); 5 else if (L > mid) return query(L, R, now << 1 | 1); 6 else return query(L, mid, now << 1) + query(mid + 1, R, now << 1 | 1); 7 //没什么好解释的吧,很好理解 8 }
那么最后再发一下例题的完整代码:
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 5e5 + 5; 5 int l[4 * maxn], r[4 * maxn]; 6 ll sum[4 * maxn]; 7 void build(int L, int R, int now){ 8 l[now] = L; r[now] = R; 9 if(L == R){ 10 scanf("%lld", &sum[now]); return; 11 } 12 int mid = (L + R) >> 1; 13 build(L, mid, now << 1); 14 build(mid + 1, R, now << 1 | 1); 15 sum[now] = sum[now << 1] + sum[now << 1 | 1]; 16 } 17 ll query(int L, int R, int now){ 18 if (L == l[now] && R == r[now]) return sum[now]; 19 int mid = (l[now] + r[now]) >> 1; 20 if (R <= mid) return query(L, R, now << 1); 21 else if (L > mid) return query(L, R, now << 1 | 1); 22 else return query(L, mid, now << 1) + query(mid + 1, R, now << 1 | 1); 23 } 24 void update(int idx, int d, int now){ 25 sum[now] += d; 26 if (l[now] == r[now]) return; 27 int mid = (l[now] + r[now]) >> 1; 28 if (idx <= mid) update(idx, d, now << 1); 29 else update(idx, d, now << 1 | 1); 30 } 31 int main(){ 32 int n, q; scanf("%d%d", &n, &q); 33 build(1, n, 1); 34 while(q--){ 35 int op, a, b; scanf("%d%d%d", &op, &a, &b); 36 if (op == 1) update(a, b - query(a, a, 1), 1); 37 else printf("%lld\n", query(a, b, 1)); 38 } 39 }
........别以为线段树就完事了,因为上面这道题只是数列中的单点修改,好像用树状数组也可以做(似乎比线段树还快,然而我没学,不管了)。
线段树还能做一件更牛的事:就是区间修改。
(先睡觉,明天更......)



