HDU7033 Typing Contest

传送门


这题比赛的时候想了好一会儿，感觉是dp，但是思考的还是不深入。

题解最后的放缩枚举范围确实厉害，自己很难想到。


首先题解很漂亮的一点就是将\(f_i\)扩大\(100\)倍，就可以避免浮点数的运算。

假设我们选定了一个大小为\(k\)的集合\(S=\{ t_1,t_2,\cdots,t_k \}\)，那么第\(i\)个人的打字速度就是\(\frac1{10000}s_{t_i}(10000 - \sum\limits_{j=1}^{k}f_{t_i} * f_{t_j} + f_{t_i} * f_{t_i})=\frac1{10000}s_{t_i}[10000 - f_{t_i}(\sum\limits_{j=1}^{k}f_{t_j} - f_{t_i})]\).

（以下为了方便，忽略了前面的\(\frac1{10000}\)）

如果\(F=\sum_{i \in S}f_{t_i}\)一定，那么每一个人的打字速度就一定了。枚举\(F\)，就变成了一个01背包：对于总容量\(F\)，每一个人的重量是\(f_i\)，价值是\(s_{t_i}[10000 - f_{t_i}(F - f_{t_i})]\).

但这样的时间复杂度太高，于是题解说，\(F\)不用枚举很多，只用到\(100\sqrt{n+2}\)即可，这样时间复杂度就是\(O(5000n^2)\)的了。接下来给出了精彩绝伦的证明：


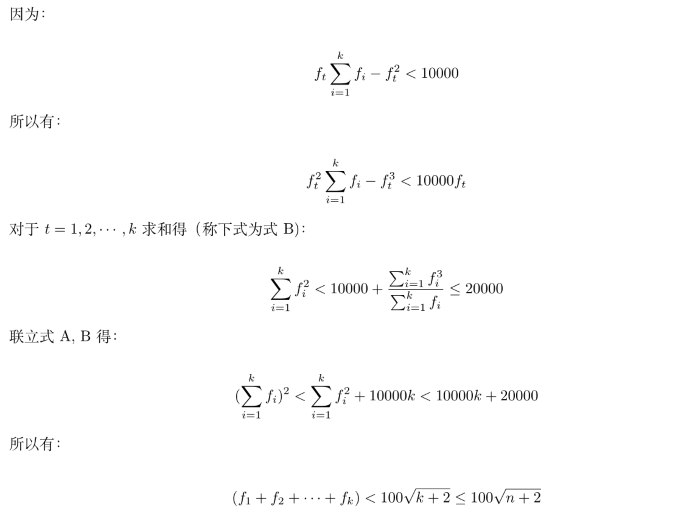
其中\(\frac{\sum_{i=1}^k f_i^3}{\sum_{i=1}^k f_i} \leqslant 10000\)这一步的放缩用到了\(\textrm{min} \{\frac{a}{b},\frac{c}{d} \} \leqslant \frac{a+c}{b+d} \leqslant \textrm{max} \{ \frac{a}{b}, \frac{c}{d}\}\).

从数学上讲，推导过程不难，但是我真的没有往这个方向上去想，长知识了。


另外代码里，头一次被浮点误差坑了。乘以\(100\)再取整数部分还真不能(int)(x*100)这么写，不信就拿x=0.57试试，他会给你保存成56.9999999.以及输出，虽然理论上只有4位小数，但是直接除以10000也出错了，不知道为什么。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<queue>
#include<assert.h>
#include<ctime>
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
#define forE(i, x, y) for(int i = head[x], y; ~i && (y = e[i].to); i = e[i].nxt)
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 105;
const int maxd = 1.5e3 + 5;
In ll read()
{
	ll ans = 0;
	char ch = getchar(), las = ' ';
	while(!isdigit(ch)) las = ch, ch = getchar();
	while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
	if(las == '-') ans = -ans;
	return ans;
}
In void write(ll x)
{
	if(x < 0) x = -x, putchar('-');
	if(x >= 10) write(x / 10);
	putchar(x % 10 + '0');
}
In void MYFILE()
{
#ifndef mrclr
	freopen("1009.in", "r", stdin);
	freopen("ha.out", "w", stdout);
#endif
}

char ff[5];
int n, f[maxn];
ll s[maxn];

ll dp[maxd];
In void solve()
{
	int sum = 0;
	for(int i = 1; i <= n; ++i) sum += f[i];
	while(sum * sum >= 10000 * (2 + n)) sum--;
	ll ans = 0;
	for(int F = 0; F <= sum; ++F)
	{
		fill(dp, dp + F + 1, 0);
		for(int i = 1; i <= n; ++i)
		{
			ll val = s[i] * (10000 - f[i] * (F - f[i]));
			if(val <= 0 || f[i] > F) continue;
			for(int j = F; j >= f[i]; --j) dp[j] = max(dp[j], dp[j - f[i]] + val);
		}
		ans = max(ans, dp[F]);
	}
	
    string ret = to_string(ans);
    while (ret.size() < 5) ret = "0" + ret;
    ret = ret.substr(0, ret.size() - 4) + "." + ret.substr(ret.size() - 4, 4);
    ret += "00000";
    cout << ret << endl;
}

int main()
{
//	MYFILE();
	int T = read();
	while(T--)
	{
		n = read();
		for(int i = 1; i <= n; ++i)
		{
			s[i] = read(); scanf("%s", ff);
     		f[i] = (ff[0] - '0') * 100 + (ff[2] - '0') * 10 + ff[3] - '0';
		}
		solve();
	}
	return 0;
}