[NOI2016]网格

嘟嘟嘟


这题前前后后写了大半个上午……


首先答案肯定是-1,0,1,2这几种。
思路就是tarjan判有无割点。因为图太大，所以考虑“离散化”，对于每一个蛐蛐，把他周围55的跳蚤拿来建图。为什么不是33呢，因为如果一个蛐蛐在边界，3*3中的方格就会把一个跳蚤算成割点。


讲道理这题就没了，但是有特别多的细节。首先得特判各种情况，比如\(n = 1\)或\(m = 1\)，只有两个相邻的块，没有蛐蛐的情况……但最为重要的是，这些特判都完事后，求出来的割点还可能是“假割点”，比如这种情况就会这么建图：

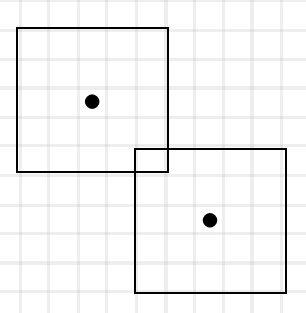
因此对于每一个割点，要判断周围有没有蛐蛐。


然后我因为用了map，花了一个多点卡常结果还是有两个点TLE了。中午吃完饭换成哈希表，这两个点只用了300ms……
所以，真爱生命，远离map！

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
#include<assert.h>
#include<ctime>
using namespace std;
#define enter puts("") 
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 1e5 + 5;
const int maxN = 2.5e6 + 5;
const int maxe = 5e7 + 5;
const ll BAS = 998244353;
const ll mod = 2333333;
In ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
In void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}
In void MYFILE()
{
#ifndef mrclr
  freopen("ha.in", "r", stdin);
  freopen("ha.out", "w", stdout);
#endif
}

#define pr pair<int, int>
#define mp make_pair

ll n, m;
int c, tot = 0;
struct Node {int x, y;}p[maxn], t[maxN];
struct Edge
{
  int nxt, to;
}e[maxe];
int head[maxN], ecnt = -1;
In void addEdge(const int& x, const int& y)
{
  //printf("-->%d %d\n", x, y);
  e[++ecnt] = (Edge){head[x], y};
  head[x] = ecnt;
}

struct Hash
{
  int head[mod], hcnt;
  pr to[maxN];
  int nxt[maxN], w[maxN];
  In void A(int x, int y, int id)
  {
    int h = (1LL * x * BAS + y) % mod;
    ++hcnt;
    nxt[hcnt] = head[h], to[hcnt] = mp(x, y), w[hcnt] = id;
    head[h] = hcnt;
  }
  In int Q(int x, int y)
  {
    int h = (1LL * x * BAS + y) % mod;
    for(int i = head[h]; i; i = nxt[i])
      if(mp(x, y) == to[i]) return w[i];
    return 0;
  }
}H;

In bool check(const int& x, const int& y)
{
  return x > 0 && x <= n && y > 0 && y <= m && ~H.Q(x, y);
}
In bool check_dis(const int& x, const int& y, const int& X, const int& Y)
{
  return abs(x - X) <= 2 && abs(y - Y) <= 2;
}

In int N(int x, int y)
{
  int tp = H.Q(x, y);
  if(!tp)
    {
      H.A(x, y, ++tot); tp = tot;
      t[tot] = (Node){x, y};
    }
  return tp;
}

int a[5][5];
const int dx[] = {-1, 0, 1, 0, -1, 1, 1, -1}, dy[] = {0, 1, 0, -1, 1, 1, -1, -1};
In void build(const int& x, const int& y, const int& X, const int& Y)
{
  int u = a[x - X + 2][y - Y + 2];
  for(int i = 0; i < 4; ++i)
    {
      int nx = x - X + dx[i] + 2, ny = y - Y + dy[i] + 2;
      if(a[nx][ny] == -1 || !check_dis(x + dx[i], y + dy[i], X, Y)) continue;
      addEdge(u, a[nx][ny]);
    }
}

In void solve(const int& x, const int& y)
{
  for(int i = -2; i <= 2; ++i)
    for(int j = -2; j <= 2; ++j)
      if((i || j) && check(x + i, y + j)) a[i + 2][j + 2] = N(x + i, y + j);
      else a[i + 2][j + 2] = -1;
  for(int i = -2; i <= 2; ++i)
    for(int j = -2; j <= 2; ++j)
      {
	if(!i && !j) continue;
	if(~a[i + 2][j + 2]) build(x + i, y + j, x, y);
      }
}

bool flg_cut = 0;
int dfn[maxN], low[maxN], cnt = 0, root;
int col[maxN], ccol = 0;
In void dfs(int now, const int& _f, const int& id)
{
  col[now] = id;
  dfn[now] = low[now] = ++cnt;
  int tp = 0;
  for(int i = head[now], v; ~i; i = e[i].nxt)
    {
      if(!dfn[v = e[i].to])
	{
	  ++tp;
	  dfs(v, now, id);
	  low[now] = min(low[now], low[v]);
	  if(low[v] >= dfn[now] && (now != root || tp > 1))
	    {
	      for(int j = 0; j < 8 && !flg_cut; ++j)
		{
		  int nx = t[now].x + dx[j], ny = t[now].y + dy[j];
		  if(nx > 0 && nx <= n && ny > 0 && ny <= m && H.Q(nx, ny) == -1) flg_cut = 1;
		}
	    }
	}
      else if(v ^ _f) low[now] = min(low[now], dfn[v]);
    }
}

In bool judge_0(const int& x, const int& y)
{
  int Col = 0;
  for(int i = -2; i <= 2; ++i)
    for(int j = -2; j <= 2; ++j)
      {
	int nx = x + i, ny = y + j;
	if((!i && !j) || !check(nx, ny)) continue;
	int tp = col[H.Q(nx, ny)];
	if(Col && Col ^ tp) return 1;
	Col = tp;
      }
  return 0;
}

In void init()
{
  ecnt = -1;
  tot = cnt = ccol = 0; flg_cut = 0;
  Mem(H.head, 0); H.hcnt = 0;
  for(int i = 1; i <= c * 25; ++i)
  dfn[i] = low[i] = col[i] = 0, head[i] = -1;
}

int main()
{
  MYFILE();
  db Beg = clock();
  int T = read();
  while(T--)
    {
      n = read(), m = read(), c = read();
      init();
      for(int i = 1; i <= c; ++i)
	{
	  p[i].x = read(), p[i].y = read();
	  H.A(p[i].x, p[i].y, -1);
	}
      for(int i = 1; i <= c; ++i) solve(p[i].x, p[i].y);
      if(!c)
	{
	  if(n * m < 3) puts("-1");
	  else puts(n == 1 || m == 1 ? "1" : "2");
	  continue;
	}
      if(n * m - c == 2)
	{
	  puts(~head[1] ? "-1" : "0");
	  continue;
	}
      if(n * m - c < 2) {puts("-1"); continue;}
      for(int i = 1; i <= tot; ++i) if(!dfn[i]) root = i, dfs(i, 0, ++ccol);
      bool flg = 0;
      for(int i = 1; i <= c && !flg; ++i)
	if(judge_0(p[i].x, p[i].y)) flg = 1;
      if(flg) puts("0");
      else
	{
	  if(n == 1 || m == 1) puts("1");
	  else puts(flg_cut ? "1" : "2");
	}
    }
  db End = clock();
  //printf("%.4lf\n", (End - Beg) / CLOCKS_PER_SEC);
  return 0;
}