[HNOI2002]营业额统计(splay基础)
嘟嘟嘟
这几天开始搞平衡树了,\(splay\)理解起来感觉还行,然而代码看了半天才勉强看懂。
我这篇博客应该不算什么入门讲解,因为我觉得我讲不明白,所以只能算自己的学习笔记吧。
这道题就是有\(n\)个数,定义\(f_i = min{|a_i - a_j|}, 1 \leqslant j < i\),其中\(f_1 = a_1\)。然后求\(\sum{f_i}\)。
解法就是每添加一个数,查找这个数的前驱和后继,然后取更小的作为\(f_i\)。因此这需要平衡树维护。
那就先简单说一下\(splay\)。
众所周知,普通的\(bst\)最坏情况下会退化成一条链,导致操作变成了\(O(n)\)。因此就有很多大佬发明了各种平衡树来保持复杂度,\(splay\)就算一种。
\(splay\)通过旋转维护树的形态,使树看起来尽量平衡,从而保持每一个操作都是\(O(\log{n})\)。
每添加一个节点\(x\),都会把\(x\)转到根,从而避免树退化成链。
具体的旋转分为右旋\((zig)\)和左旋\((zag)\),然后不同的情况这两种旋转的顺序也会不一样。
第一种:
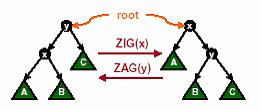
(感谢\(gg\)的图)
这个图已经表达的很明白了,如果\(x\)的父亲就是根节点的话,旋转一次即可,根据方向用\(zig\)或者\(zag\)。
第二种:
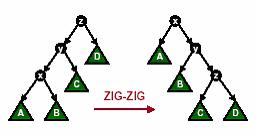
更多的是\(x\)的父亲不是根节点,这种情况是\(x\)和\(y\)在\(y\)的父亲\(z\)的同侧。这个时候要旋转两步,先把\(y\)旋转到\(z\)上,再把\(x\)旋转到\(y\)上。
第三种:
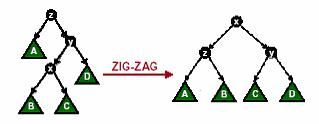
这个是\(y\)在\(z\)的一侧,而\(x\)在\(y\)的另一侧。这个时候应该先把\(x\)旋转到\(y\)上,在把\(x\)旋转到\(z\)上。至于为什么这个顺序,我也不是很清楚。但是反正这样转完后看起来确实很平衡。
理解起来好像还行。但是代码就不太友善了。我学的是把\(zig\)和\(zag\)放一块的写法,代码精简但比较难懂,估计还得消化一阵子吧。
我觉得理解起来的关键就是不要想是左还是右,而是用“这个儿子”和“另一个儿子”去表示。
void pushup(int now)
{
t[now].siz = t[t[now].ch[0]].siz + t[t[now].ch[1]].siz + t[now].cnt;
}
bool get(int x)
{
return t[t[x].fa].ch[1] == x;
}
void rotate(int x)
{
int y = t[x].fa, z = t[y].fa, k = get(x); //k:x是y的哪一个儿子
t[z].ch[t[z].ch[1] == y] = x; t[x].fa = z; //z的儿子从y换成x,就是
t[y].ch[k] = t[x].ch[k ^ 1]; t[t[y].ch[k]].fa = y;
//如果x是y的右儿子,那么y的右儿子现在变成了x的左儿子
t[x].ch[k ^ 1] = y; t[y].fa = x;
//然后x的右儿子现在是y
pushup(x); pushup(y);
}
void splay(int x, int s) //把x旋转到s,这题s传的都是0
{
//注意:树的根其实是0号节点的孩子,之所以传0,是为了写的方便
while(t[x].fa != s)
{
int y = t[x].fa, z = t[y].fa;
if(z != s) //这表示的是x还得再转两次,所以如果s就是根的话,转一次的情况就不直到怎么判了
{
//x, y同向先转y,否则先转x
//额外转一次
if((t[y].ch[0] == x) != (t[z].ch[0] == y)) rotate(x);
else rotate(y);
}
rotate(x); //在转一次
}
if(!s) root = x; //只有x要转到根的时候才更新根
}
\(splay\)函数我得再说一下。就是他不仅可以旋转到根,到任意一个祖先节点都行,但是这道题只用旋转到跟就行了。
然后是几个基本操作:
1.插入权值为\(x\)的元素
如果当前节点大于\(x\),就向左递归,否则向右,如果已经有了,就停止。
所以每一个节点有一个\(cnt\),记录权值为\(val\)的数有多少个。
如果没有,就要新建节点,具体看代码好了。
bool insert(int x) //非递归版
{
int now = root, f = 0;
bool flg = 0; //flg是因为这道题需要,跟splay没有关系
while(now && t[now].val != x) f = now, now = t[now].ch[x > t[now].val];
if(now) t[now].cnt++, flg = 1; //这个数已经有了
else
{
now = ++ncnt;
if(f) t[f].ch[x > t[f].val] = now; //来个判断是为了整棵树还没有节点的情况
t[now].fa = f;
t[now].ch[0] = t[now].ch[1] = 0;
t[now].val = x;
t[now].siz = t[now].cnt = 1;
}
splay(now, 0);
return flg;
}
2.查找权值为\(x\)的元素
这个很简单,
代码里找到后顺便旋了上去,这个是为了找前驱后继用的。
void find(int x)
{
int now = root;
if(!now) return;
while(t[now].ch[x > t[now].val] && t[now].val != x) now = t[now].ch[x > t[now].val];
splay(now, 0);
}
3.找\(x\)的前驱,后继
我的做法是先找到\(x\),然后把他旋到根(此题保证\(x\)存在),这样的话找前驱就是走一步左儿子,再右儿子一直走到底。
后继同理:走一步右儿子,然后左儿子走到底。
int pre(int x)
{
find(x); //找到并把x旋到根
int now = t[root].ch[0];
while(t[now].ch[1]) now = t[now].ch[1];
return t[now].val;
}
int nxt(int x)
{
find(x);
int now = t[root].ch[1];
while(t[now].ch[0]) now = t[now].ch[0];
return t[now].val;
}
这道题只用到这几个操作,所以我就说这么多啦。 最后发一下完整代码 ```c++ #include
int n, ans = 0;
struct Tree
{
int ch[2], fa;
int siz, cnt, val;
}t[maxn << 1];
int root = 0, ncnt = 0;
void pushup(int now)
{
t[now].siz = t[t[now].ch[0]].siz + t[t[now].ch[1]].siz + t[now].cnt;
}
bool get(int x)
{
return t[t[x].fa].ch[1] == x;
}
void rotate(int x)
{
int y = t[x].fa, z = t[y].fa, k = get(x);
t[z].ch[t[z].ch[1] == y] = x; t[x].fa = z;
t[y].ch[k] = t[x].ch[k ^ 1]; t[t[y].ch[k]].fa = y;
t[x].ch[k ^ 1] = y; t[y].fa = x;
pushup(x); pushup(y);
}
void splay(int x, int s)
{
while(t[x].fa != s)
{
int y = t[x].fa, z = t[y].fa;
if(z != s)
{
if((t[y].ch[0] == x) != (t[z].ch[0] == y)) rotate(x);
else rotate(y);
}
rotate(x);
}
if(!s) root = x;
}
bool insert(int x)
{
int now = root, f = 0;
bool flg = 0;
while(now && t[now].val != x) f = now, now = t[now].ch[x > t[now].val];
if(now) t[now].cnt++, flg = 1;
else
{
now = ++ncnt;
if(f) t[f].ch[x > t[f].val] = now;
t[now].fa = f;
t[now].ch[0] = t[now].ch[1] = 0;
t[now].val = x;
t[now].siz = t[now].cnt = 1;
}
splay(now, 0);
return flg;
}
void find(int x)
{
int now = root;
if(!now) return;
while(t[now].ch[x > t[now].val] && t[now].val != x) now = t[now].ch[x > t[now].val];
splay(now, 0);
}
int pre(int x)
{
find(x);
int now = t[root].ch[0];
while(t[now].ch[1]) now = t[now].ch[1];
return t[now].val;
}
int nxt(int x)
{
find(x);
int now = t[root].ch[1];
while(t[now].ch[0]) now = t[now].ch[0];
return t[now].val;
}
int main()
{
n = read();
insert(INF); insert(-INF);
int x = read(); ans += x; insert(x);
for(int i = 2; i <= n; ++i)
{
int x = read();
if(insert(x)) continue;
int a = pre(x), b = nxt(x);
ans += min(x - a, b - x);
}
write(ans), enter;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号