微积分第一章_极限

1. 函数

 

映射，无穷小，无穷大。

奇偶性，单调性，间断点，连续性，复合函数，渐*线，零点。

 

间断点，分段点（英语：Discontinuities），通常是在单变数实变函数的环境下讨论。

根据不同不连续点的性质，通常把不连续点分为两类：

1. 第一类不连续点：
   1. 可去不连续点：不连续点两侧函数的极限存在且相等 。
   2. 跳跃不连续点：不连续点两侧函数的极限存在，但不相等；
2. 第二类不连续点：

不属于第一类不连续点的任何一种不连续点都属于第二类不连续点。第二类不连续点可以进一步分为无穷不连续点和震荡不连续点。

渐*线分为三种类型：水*，垂直和倾斜。对于由函数y =ƒ（x）的图给出的曲线，水*渐*线是水*线，函数的图随着x趋于+∞或-∞趋*于水*线。垂直渐*线是垂直线，函数在该垂直线附*无限增长。斜渐*线的斜率非零但有限，因此当x趋于+∞或-∞时，函数的图接*该斜率。

 

渐*线传达有关大曲线特性的信息，确定函数的渐*线是绘制函数图的重要步骤。从广义上讲，对功能渐*线的研究是渐*分析主题的一部分。当任意曲线上一点沿曲线无限远离原点时，如果到一条直线（或另外一条曲线）的距离无限趋*于零，那么这条直线（曲线）称为这条曲线的渐*线。数学上的定义则是：若函数的图形收敛，则渐*线为。

 

2.函数极限的计算。

 

首先知道七种不定式的类型

每种不定式类型，都有对应的方法解决。

 

 

 

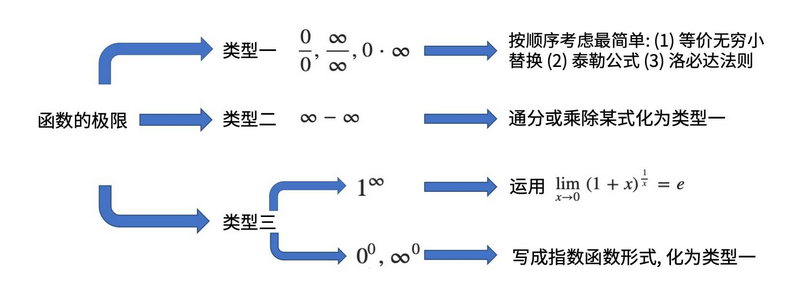
 主要有以下方法

 

等价无穷小替换方法。

泰勒公式

洛必达

重要极限方法

写成指数形式

 

3.无穷小量与无穷小量的比较。

 

其他：

1. 极限综合题

　　  2.边角的知识点。