分治法与归并排序

本文部分内容参考了《算法导论》

分治策略

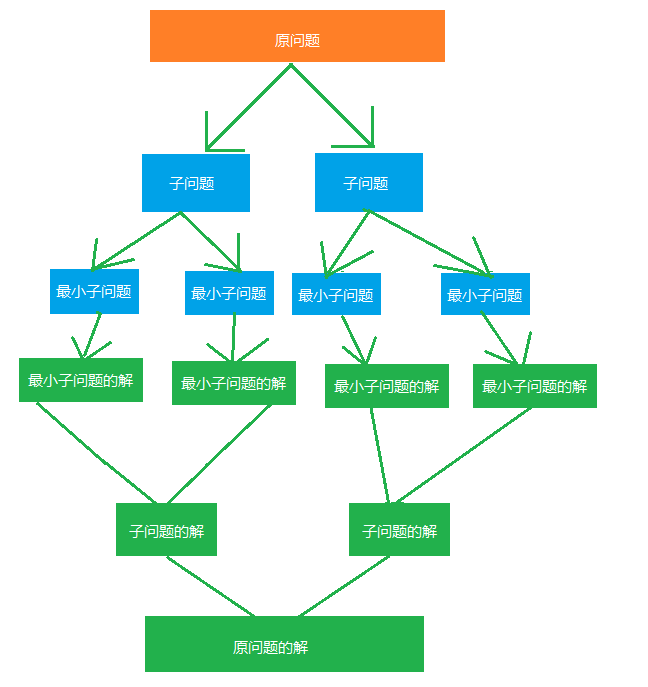
　　解决一个给定问题，算法需要一次或多次地递归调用自身来解决相关的子问题，这种算法通常采用分治策略。分治模式在每一层递归上都有三个步骤：

　　〉〉分解：将原问题分解成一系列子问题

　　〉〉解决：递归地求解各子问题。若子问题足够小，则直接求解

　　〉〉合并：将子问题的结果合并成原问题的解。

 

归并排序（合并排序）

　　归并排序的关键在于归并两个相邻的子序列，使其变成一个排序好的新序列。如果这个新序列就是原来需要进行排序的数组，那么排序完成。所以，我们需要将原序列递归地分成若干子序列，直道最小的子序列只有一个元素，然后将子序列依次归并，就可以得到排序好的原序列。

归并两个子序列

　　我们要解决的第一个问题就是：假设有子序列A[p...q]和子序列[q + 1...r]是已经排序好的子序列，如何按顺序将它们归并到一个子序列中去呢？

　　我们可以用扑克牌做模拟。将两堆数量相近的扑克牌按顺序叠好，最小的牌放在最上面，牌面朝上。

　　〉〉第一步：拿出两张中较小的一张，放在桌上。

　　〉〉第二步：分别比较所拿的牌和两个堆上面的牌，重复第一步，跟在前一张牌的后面。直到一个堆拿完。

　　〉〉第三步：将剩余的堆从上往下一次放在桌上，跟在前一张牌的后面。

　　由此可见，按问题要求（加橙色的），我们可以设计如下代码：

void merge(int ar[], int p, int q, int r, int temp[]){
        //将ar[p...q]和ar[q+1...r]合并到temp[p...r],temp由外部分配内存
    int i = p, j = q + 1, k = 0;
    while(i <= q && j <= r){
        if(ar[i] < ar[j])
            temp[k++] = ar[i++];
        else
            temp[k++] = ar[j++];
    }
    while(i <= q) //如果ar[p..q]有剩
        temp[k++] = ar[i++];
    while(j <= r) //如果ar[q+1..r]有剩
        temp[k++] = ar[j++];

    for(k = 0; k <= (r - p); k++) //将合并后的子序列赋值给原序列ar[p...r]
        ar[p + k] = temp[k];
}

　

利用分治策略使原序列有序

　　对于归并排序，我们要解决的第二个问题就是：原序列如何成为有序序列？

　　我们可以通过将原序列二分为两个子序列，再将两个子序列二分为另外的四个子序列，直到不能再分解为止。然后分别合并相邻的两个子序列，直到不能合并为止。这里引用网络上的一张图修改后来说明这个原理。

 

 　　前面提到过，解决一个给定问题，算法需要一次或多次地递归调用自身来解决相关的子问题，这种算法通常采用分治策略。所以，我们可以利用分治策略通过通过递归调用一个函数来解决。我们可以这样写代码：

void mergesort(int ar[], int head, int end, int temp[]){
    if(head < end){ //条件：直到不能分割为止
        int middle = (head + end) / 2; //找到二分原序列的点
        mergesort(ar, head, middle, temp); //左子序列排序
        mergesort(ar, middle + 1, end, temp); //右子序列排序
        merge(ar, head, middle, end, temp); //合并这两个子序列
    }
}

 　　分析上面的代码，我们可以将上图标上执行顺序，来验证该算法的正确性。同时，你也可以通过类似“循环不变式”的方法证明：

完整代码

　　到这里，归并排序的所有问题都解决完了。我们给出完整的不带注释（分配内存后的空注释是标志，提醒一定要及时释放内存）的代码。

　　*说明一下，MergeSort中的mergesort()函数和更好的MergeSort中的_mergesort()函数中并没有创建middle变量来存储二分原序列的点，原因是在递归调用函数时我们应尽量避免创建不太需要的变量导致内存占用的飙升（浪费）。

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <time.h>

void mergesort(int [], int, int, int []);
void merge(int [], int, int, int, int[]);

int main(int argc, char * argv[]){
    int * ar, * temp;
    int n = 10, i;

    if( !(ar = (int *)malloc( (size_t)n * sizeof(int) ) ) )//
        exit(EXIT_FAILURE);
    if( !(temp = (int *)malloc( (size_t)n * sizeof(int) ) ) )//
        exit(EXIT_FAILURE);

    srand( (unsigned int)time(NULL) );
    for(i = 0; i < n; i++){
        ar[i] = rand() % 1000;
        printf("%-4d",ar[i]);
    }

    mergesort(ar, 0, n - 1, temp);

    printf("\n归并排序后:\n");
    for(i = 0; i < n; i++)
        printf("%-4d",ar[i]);

    free(temp);
    free(ar);

    _getch();
    return 0;
}

void mergesort(int ar[], int head, int end, int temp[]){
    if(head < end){
        int middle = (head + end) / 2;
        mergesort(ar, head, middle, temp);
        mergesort(ar, middle + 1, end, temp);
        merge(ar, head, middle, end, temp);
    }
}

void merge(int ar[], int p, int q, int r, int temp[]){
    int i = p, j = q + 1, k = 0;
    while(i <= q && j <= r){
        if(ar[i] < ar[j])
            temp[k++] = ar[i++];
        else
            temp[k++] = ar[j++];
    }
    while(i <= q)
        temp[k++] = ar[i++];
    while(j <= r)
        temp[k++] = ar[j++];

    for(k = 0; k <= (r - p); k++)
        ar[p + k] = temp[k];
}

 　　下面这个是带有入口函数的，只要在main()函数中把数组名和大小传递给mergesort()函数就行了。

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#include <time.h>

void mergesort(float *, int);
void _mergesort(float *, int, int, float *);
void merge(float *, int, int, int, float *);

int main(int argc, char * argv[]){
    float * ar;
    int n = 10, i;

    if( !(ar = (float *)malloc( (size_t)n * sizeof(float) ) ) )//
        exit(EXIT_FAILURE);

    srand( (unsigned int)time(NULL) );
    for(i = 0; i < n; i++){
        ar[i] = (float)((rand() % 499)) / (float)((rand() % 11 + 1));
        printf("%-6.3g",ar[i]);
    }

    mergesort(ar, n);

    printf("\n归并排序后:\n");
    for(i = 0; i < n; i++)
        printf("%-6.3g",ar[i]);

    free(ar);

    _getch();
    return 0;
}

void mergesort(float * ar, int size){
    if(size > 0){
        float * temp;
        if(!(temp = (float *)malloc( (size_t)size * sizeof(float) ) ) ) //
            exit(EXIT_FAILURE);
        _mergesort(ar, 0, size - 1, temp);
        free(temp);
    }
}

void _mergesort(float * ar, int head, int end, float * temp){
    if(head < end){
        _mergesort(ar, head, (head + end) / 2, temp);
        _mergesort(ar, (head + end) / 2 + 1, end, temp);
        merge(ar, head, (head + end) / 2, end, temp);
    }
}

void merge(float * ar, int p, int q, int r, float * temp){
    int i = p, j = q + 1, k = 0;
    while(i <= q && j <= r){
        if( ar[i] < ar[j] )
            temp[k++] = ar[i++];
        else
            temp[k++] = ar[j++];
    }
    while(i <= q)
        temp[k++] = ar[i++];
    while(j <= r)
        temp[k++] = ar[j++];

    for(k = 0; k <= (r - p); k++)
        ar[p + k] = temp[k];
}