小猫爬山问题---贪心算法失效，深度优先搜索优化

提示

　　小猫爬山问题正解在文章最后部分，如果对求解的曲折过程不感兴趣，可直接跳到文末。

问题描述

　　小猫爬山问题是这样的：有n只小猫，每只小猫的质量分别为cat1, cat2, … ,cat n，现在它们已经爬到山顶，筋疲力尽，需要乘坐缆车下山（缆车只有一辆）。缆车最大载重量为w。问总共最少需要坐几趟多少缆车。

　　这题需要我们编程求解，

输入格式为：

　　第一行包含两个用空格隔开的整数，n和w。
　　接下来n行每行一个整数，其中第i+1行的整数表示第i只小猫的质量​。

输出格式为：

　　输出一个整数，表示最小需要的趟数。

贪心算法失效的论证

初次接触这类问题，我们一般倾向于利用贪心算法的思想寻找解决思路。一种粗暴的想法是，把这些猫的质量相加，再看看需要多少趟车才能运完。这样想的话：

 

 

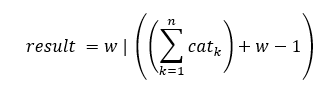
这里“|”表示整除。但是，一只猫不应被杀死而分块运走。如缆车载重量为6，猫有三只，质量为5,4,3,按照公式，只要2趟即可完成。但是，仔细一想，便觉恐怖。实际上，这个情况需要运3趟。这个暴力方法不能用。

　　　当然，更好的贪心思路解法是，我们先根据质量大小对猫进行排序，按照从小到大或从大到小的顺序装车运走。但这个想法并不符合题意。我们仅看一个反例：缆车载重量为9，猫有9只，质量分别为1,2,3,4,5,6,7,8,9，按照这次“不残暴”的贪心思路（对于本反例，无论从大到小还是从小到大，均能得到下面的结果），应该分为6趟车运走：(1+2+3), (4+5), (6), (7), (8), (9) 。但实际上，5趟足矣：(1+8), (2+7), (3+6), (4+5), (9) 。因此，这个方法也不能用。

利用深搜解决及解法优化

　　　 如果我们能把所有的分配情况都列举出来，一定能找出用车最少得情况，最终求出最少需要的趟数。这时，我们需要考虑深度优先搜索算法。深度优先搜索算法，简单地说就是一种能穷举所有可能结果的算法：这个算法可以通过函数递归实现，先通过不断的迭代获得一种结果，接着回溯，再迭代得到另一种结果；不断进行上述操作，直到获得所有结果。在取得每种结果时，可以获得解决问题所需要的信息，当然，我们也可以通过一些条件判断终止某类结果的求解过程，以节省时间与空间，这被称为“剪枝”。深度优先搜索是一种图论算法，我们可以在讲授算法的书中找到它的更严格，更一般的定义。

    我们可以通过从小到大枚举所用缆车的数量，并逐个验证缆车是否够用，来求出所需要的最少的缆车数量。因为，缆车够用即意味着每一只猫都能装在缆车中，我们只需要将每只猫在哪个缆车的所有情况列出，就可以直到缆车是否够用。

    于是，我们可以写出判断缆车是否够用的函数的代码：

bool check(int num_cat, int num_car) { //判断缆车数是否够用，num_cat猫的编号，num_car车的数量
    if (num_cat >= n)    return true; //如果猫的编号等于猫的数量，说明已经把0~n-1共n只猫全部放入缆车，缆车够用
    else {
        bool ava = false; //用于找到可行方案后终止搜索
        for (int i = 0; i < num_car; ++i) { //将猫放在不同缆车的情况进行枚举
            if (car[i] + cat[num_cat] <= w) { //如果某个缆车能放下这只猫
                car[i] += cat[num_cat]; //放下去
                ava = check(num_cat + 1, num_car); //开始放下一只猫
                if (ava) break; //如果这次放猫能导出可行方案，就终止搜索
                else car[i] -= cat[num_cat]; //否则，这只猫不能放这个缆车
            }
        }
        return ava; //所有情况都列出后，返回是否可行
    }
}

　　　　一般来说，对于输入的猫的重量，我们可以直接使用。但是，恰当的顺序有利于减小程序的运行时间。

对于极端的输入数据：“18 100000000 18381246 29249683 12495474 24844134 96242521 67846996 945213 27675252 58653213 12062801 4830609 83790642 10682393 27267295 60527976 8881456 3916444 32450339”，在笔者的电脑上，测试数据如下：

 

情形	最终答案	耗时
不对猫的质量进行排序	6	0.308s
猫的质量从大到小	6	0.001s
猫的质量从小到大	6	860s

但是，按照这个思路写的代码提交到nowcoder的oj上测试时，超时了。

   超时，很大一部分是枚举导致的，因为在缆车数从1到n枚举的过程中，不可避免地出现重复的验证过程，造成时间上的额外开销。我们换个思路：直接求解所需的最小缆车数。

   为此，我们仍然从列举每只猫放在哪个缆车的所有情况出发，只不过，这回，缆车的数量不是个定值。为了减小求解过程，我们将猫的质量从大到小排序，相比于不排序，这样做可以让我们用更少的时间求出所用缆车的最小结果，并“剪枝”掉大量的搜索过程。完整的AC代码如下：

#include <iostream>
#include <algorithm>

int n, w;
int cat[25], car[25];

int solve(int num_cat, int car_used) { //num_cat猫的编号 car_used放了猫的车的数量
    //这里，car_used处值为1，即一开始一定有一个缆车被放猫，我们也把这个缆车的编号看作1
    static int ans = n; //静态变量，用于存储、更新最佳答案，并及时终止多余的搜索
    //由于缆车数不可能超过猫的总数n，因此取ans初值为n
    if (car_used < ans) { //在用车数少于ans时，才可能求得更优的解
        if (num_cat == n) ans = car_used; //若此时猫已放完，最佳答案更新为此时所用车数
        else {
            for (int i = 1; i <= car_used; ++i) {//对于当前的猫，我们可以放在已经放过猫的缆车上
                if (car[i] + cat[num_cat] <= w) {
                    car[i] += cat[num_cat];
                    solve(num_cat + 1, car_used);
                    car[i] -= cat[num_cat]; //注意回溯
                }
            }
            car[car_used + 1] = cat[num_cat]; //也可以把当前的猫放在新的缆车里
            solve(num_cat + 1, car_used + 1);
            car[car_used + 1] = 0; //注意回溯
        }
    }
    return ans; //永远返回最佳答案
}

int main() {
    std::cin >> n >> w;
    for (int i = 0; i < n; ++i)
        std::cin >> cat[i];
    
    std::sort(cat, &cat[n], std::greater<int>());
    std::cout << solve(0, 1);

    return 0;
}

　　以深度优先搜索为中心的两种思路都能解决小猫爬山问题，但是显然后者对大数据和极端输入更具优势。在直接求解最小缆车数的过程中，由于我们事先已经对猫的质量进行从大到小的排序，因此，对于要被放入缆车的猫而言，依然有可能进入之前已经放了猫的缆车中，所以不能简单地将放置情形简化为：要么放在当前的缆车，要么放在下一个缆车。

　　如果我们将猫的质量从小到大排序，则可以作上面的简化。但是，这样写出的程序不能列出大猫小猫一起放的情形。也就是说，这么写的程序与第二种贪心思路写出的程序会出现一样的错误。故不可取。