「数据挖掘入门系列」数据挖掘模型之分类与预测 - 决策树
决策树在分类、预测、规则提取等领域有着广泛的应用。
决策树是一种树状结果,它的每一个叶节点对应一个分类。构造决策树的核心问题是:在每一步如何选择适当的属性对样本做拆分。对于分类问题,从已知类标记的训练样本中学习并构造出决策树是一个自上而下,分而治之的过程。
常见的决策树算法如下:
- ID3算法
- C4.5算法
- CART算法
其中ID3是最经典的决策树分类算法。
ID3算法
ID3算法基于信息熵来选择最佳测试属性。它选择当前样本集中具有最大信息增益值的属性作为测试属性。
总的信息熵计算方式如下:
设S是s个数据样本的集合。假定某个类别有m个不同的取值:Ci(i = 1, 2, …, m)。设Si是某个类别Ci中的样本数。对于一个给定样本,它总的信息熵为:
其中,Pi是任意样本属于Ci的概率,一般可以用Si/s估计。
每个属性的信息熵计算方式如下:
假设一个属性A具有k个不同的值{a1, a2, …, ak},利用属性A将集合S划分为若干个子集 {S1, S2, …, Sk},其中Sj包含了集合S中属性A取aj值的样本。若选择属性A为测试属性,则这些子集就是从集合S的节点生长出来的新的叶子节点。设Sij是子集Sj中类别为Ci的样本数,则根据属性A划分样本的信息熵值为:
最后,用属性A划分样本集S后所得的信息增益(Gain)为:
Gain值越大,说明选择测试属性A对于分类提供的信息越大,选择A之后对于分类的不确定程度越小。
ID3算法具体流程
- 对当前样本集合,计算所有属性的信息增益(总的信息熵)
- 选择信息增益最大的属性作为测试属性,把测试属性取值相同的样本划分为同一个样本集
- 若子样本集的类别属性只含有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用出;否则对子样本集递归调用本算法
决策树案例
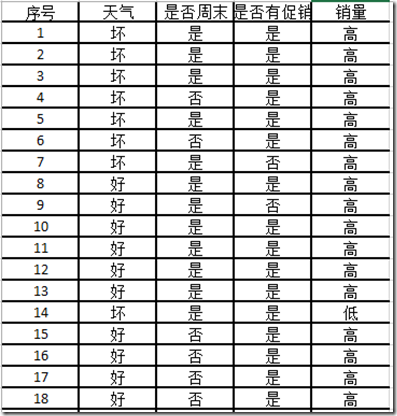
接下来通过一个案例来了解天气、是否周末、是否有促销对销量的影响。数据集格式如下:
数据集已经上传到百度云盘:https://pan.baidu.com/s/1zX9W0XC3arA0L2HqrjQR7g
计算信息熵值
1、计算总的信息熵值
销量有两种分类为:Ci = {高, 低}, 其中销量为高的为18个,销量为低的是16个。
故总的信息熵为:
通过以下Python代码计算总的信息熵值为:0.997502546369
#-*- coding: utf-8 -*- import math as m # 计算总的信息熵 I_18_16 = -18 / 34.0 * m.log(18 / 34.0, 2) - 16 / 34.0 * m.log(16 / 34.0, 2) print I_18_16
2、计算每个测试属性(天气、是否周末、是否有促销)的信息熵值
2.1 天气
天气好的情况:销量高的有11个,销量低的有6个
天气坏的情况:销量高的有7个,销量低的有10个
分别计算天气好和天气坏的信息熵为:
天气好的信息熵为:0.936667381878
天气坏的信息熵为:0.964078764808
天气属性的信息熵为:0.950373073343
计算属性「天气」属性的增益值为:
Gain(天气) = 0.0471294730262
同理,通过以上方式,我们可以计算得到「是否周末、是否有促销」的增益值,分别为:
天气属性的增益值为:0.047129
是否周末属性的增益值为:0.139394
是否有促销属性的增益值为:0.127268
故增益最大的属性为:是否为周末。
基于以上结论,以是否为周末作为根节点来构建决策树。
计算代码如下:
#-*- coding: utf-8 -*- import math as m # 计算二分类信息熵 # s1, s2必须是浮点数 def calc(s1, s2): return - s1 / (s1 +s2) * m.log(s1 / (s1 +s2), 2) - s2 / (s1 +s2) * m.log(s2 / (s1 +s2), 2) # 计算总的信息熵 print u'总的信息熵为:' print calc(18.0, 16.0) print '- -' * 10 print '天气属性信息熵与增益值计算' # 计算天气好的信息熵为 print calc(11.0, 6.0) # 计算天气坏的信息熵为 print calc(7.0, 11.0) # 计算天气属性的信息熵为 come_weather = 17 / 34.0 * calc(11.0, 6.0) + 17 / 34.0 * calc(7.0, 11.0) print come_weather # 计算天气属性的增益值为 print '天气属性的增益值为:%f' % (calc(18.0, 16.0) - come_weather) print '- -' * 10 print '是否周末属性信息熵与增益值计算' # 计算是周末的信息熵为 print calc(11.0, 3.0) # 计算不是周末的信息熵为 print calc(7.0, 13.0) # 计算是否周末属性的信息熵为 come_weekday = 14 / 34.0 * calc(11.0, 3.0) + 20 / 34.0 * calc(7.0, 13.0) print '是否周末属性的增益值为:%f' % (calc(18.0, 16.0) - come_weekday) print '- -' * 10 print '是否有促销属性信息熵与增益值计算' # 计算有促销的信息熵为 print calc(15.0, 7.0) # 计算不是周末的信息熵为 print calc(9.0, 3.0) # 计算是否周末属性的信息熵为 come_sales = 22 / 34.0 * calc(15.0, 7.0) + 12 / 34.0 * calc(9.0, 3.0) print '是否有促销属性的增益值为:%f' % (calc(18.0, 16.0) - come_sales)
使用python构建决策树模型
# -*- coding: utf-8 -*- import sys reload(sys) sys.setdefaultencoding('utf-8') # 1. 导入pandas库 import pandas as pd # 2.读取excel数据 data = pd.read_excel('sales_data.xls', index_col=u'序号') # 3. 数据是类别标签,需要将数据转换为数字 # 用1表示好、是、高 # 用-1表示坏、否、低 data[data == u'好'] = 1 data[data == u'是'] = 1 data[data == u'高'] = 1 data[data != 1] = -1 # 3.1 获取除索引列以外的3列 x = data.iloc[:,:3].as_matrix().astype(int) # 3.2 获取销量列 y = data.iloc[:,3].as_matrix().astype(int) # 4. 导入决策树模型 from sklearn.tree import DecisionTreeClassifier as DTC # 5. 构建基于信息熵的决策树模型 dtc = DTC(criterion='entropy') # 6. 训练模型 fit = dtc.fit(x, y)


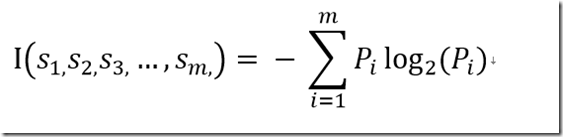

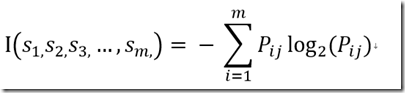
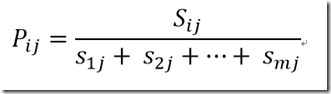
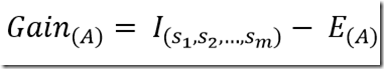
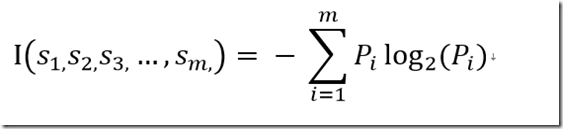
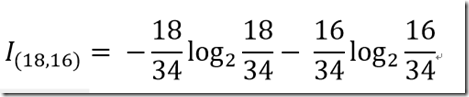
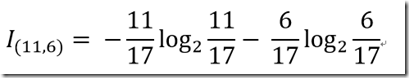
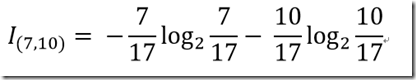

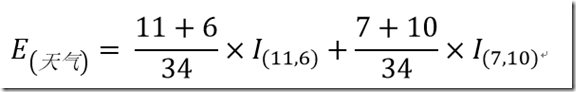
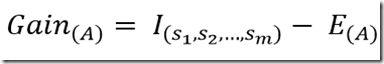

 浙公网安备 33010602011771号
浙公网安备 33010602011771号