充分条件和必要条件

充分条件：

如果条件A是结论B的充分条件：A与其他条件是并连关系，即A、C、D….中任意一个存在都可以使得B成立（就像是个人英雄主义），如下图：

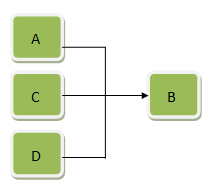
用法推导：

1．如果条件A存在，B肯定成立，即A→B（箭头表示能够推导出）

2．如果B不成立，则说明所有可能的条件都不存在，因此A肯定也不存在，即非B→非A

3．如果条件A不存在，而条件C、D可能存在，也可以使得B成立，即不能导出非A→非B

 

必要条件：

条件A是结论B的必要条件：A与其他条件是串联关系，即条件A必须存在，且条件C、D….也全部存在才可能导致B结论。（团结的力量）如下图：

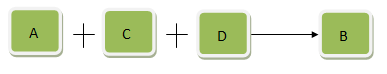
用法推导：

我简单表示为A+…→B(中间的点表示还有其他条件)

1．如果B成立了，说明所有条件都存在，肯定存在条件A。即B→A。

2．如果条件A不存在，串联少了一个条件，B也肯定不能成立，即 非A→非B。

3．如果B不成立，可能是C，D不存在但A存在，只是C、D掉链子了，即不能导出 非B→非A。

 

试题中的用法：

先判断出各个关键词之间是充分还是必要关系，然后用关键词和箭头画出之间的关系，例如：A是B的充分条件，A’是B的必要条件，则画出来A→B←.....+A’，然后根据必要条件A’+…→B能推导成B→A’的特点转化为A→B→A’

然后根据四个正确推论：A→B ，非B→非A，B→A’，非A’→非B和

两个错误推论：非A→非B ，非B→非A’即可进行判断。

 

对于公务员考试中此类题的简单解题方法，我在专栏里做了详细介绍，需要的话请移步专栏：充分必要条件 - 简单解题方法，如果完全理解消化了的话，应该就能很顺利地解决这类题目了。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

 

印象中这是当年高一数学课本上的知识。

充分条件

充分不必要条件

必要条件

必要不充分条件

充要条件

既不充分又不必要条件

 

充分条件：

只要有A，就一定能达成B，A是B的充分条件。

充分不必要条件:有A，一定能达到B；就算没有A，也有可能达到B。

举例：某次考试，试卷满分为100分。小明考了90分。对于“及格”这件事来说，90分是“充分条件”；再细致一点说的话，“及格”并不需要90分那么多，就算再少一点，也可能及格，也就是说，90分是及格的“充分不必要条件”。

 

必要条件：

如果能做到A，则必定做到了B，B是A的必要条件。

必要不充分条件：如果能做到A，则必定能做到B，但如果只做到B的话，还不够做到A。

举例：某次考试，满分为100分，第一道的分值为41分（或41分以上），题目是个单选题：“本门课的任课老师是谁？”备选项是4张大头照。

小明如果想及格，则必须做对这道单选题。也就是说，做对第一题是这堂考试及格的必要条件。

可问题是小明经常翘课，只在考前最后一堂课时奔着“划重点”的目标去点个卯，结果老师说“俺向来不给划重点”，恨得小明牙痒痒地，一边百无聊赖地转笔，一边死盯着老师的脸，心里恨恨地想着“我从未见过如此厚颜无耻之人”。所以呢，到了考试时，虽然第一题做对了，但后面的题目完全无从下笔。也就是说，做对第一题是这堂考试及格的必要不充分条件。

 

充要条件：

如果能做到A，则必定能做到B；如果做到了B，则必定能做到A，A、B互为对方的充要条件。

强调一下，在说“充要条件”的时候，必定是“互相”的。

举例：某次考试，满分为100分，出题老师玩了一把行为艺术，第一道题的分值为60分（或60分以上），题目仍然是那道“本门课的任课老师是谁”的单选题。

如果想及格，就必须做对这道题；如果做对了这道题，则必然能及格。也就是说“做对这道题”与“这次考试及格”互为“充要条件”。

 

既不充分又不必要条件：

直接上例子吧：

还是那门课考试，结果呢学校的有关部门提前核查了一下试卷，对出题老师的行为艺术提出了异议，于是出题老师修改了分值，保留了那道单选题，但改成了10分（只要40分以下都可以）。

于是班上有的人上过课（经常上课或偶尔上课都可以），做对了第一题，但后面的题目丢分太多，总分达不到60，仍然不及格；班上还有学神学霸，虽然从不上课，第一题猜答案时也猜错了，但后面的题目基本上都做对了，总分在60分以上。

也就是说，对于这个班的学生来说，“做对第一题”是“考试及格”的既不充分又不必要条件。

 

出处：https://www.zhihu.com/question/30469121