前缀和and差分

---

1.前缀和

求前缀和的时间复杂度与数据的规模有关，但是用前缀和去求某一区间的和时间复杂度为O(1)

一维：

• 一般让下标从1开始，可以避免特判

• 一维前缀和 s[i]=a[1]+a[2]+……+a[i]

• 求数组[l,r]之间的和 =s[r]-s[l-1]

二维：

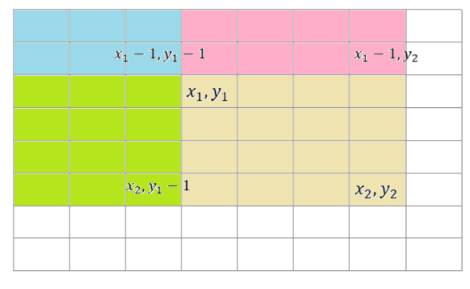
• 二维前缀和s[i][j]=a[i][j]+s[i][j-1]+s[i-1][j]-s[i-1][j-1]
• 求[x1,y1]到[x2,y2]的和=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]

2.差分

给出一串数a[n]，构造差分b[n], 使得a[i]=b[1]+b[2]+……+a[i],可以将差分看作前缀和的逆运算，那么称b数组是a数组的差分

一维

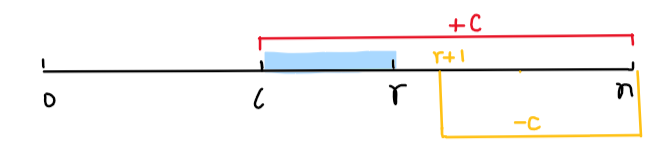
这样当我们需要给a数组中的区间[l,r]都加上c，只需要将b[l]+c、b[r+1]-c，时间复杂度为O(1)，即使有n次这样的操作时间复杂度还是O(1)，那么最后只需要对b数组求一遍前缀和就可以得到操作完的a数组

void insert(int l,int r,int c)
{
    b[l]+=c;
    b[r+1]-=c;
}

for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1]; //构造差分数组b
……insert操作
for(int i=1;i<=n;i++) a[i]=b[i]+a[i-1];//a数组

二维：

类似于一维，如果要将[x1,y1]到[x2,y2]区间中的数都加上c，只需要将b[x1,y1]+=c、b[x2+1,y1]-=c、b[x1,y2+1]-=c、b[x2+1,y2+1]+=c

参考二维前缀和