蓝桥杯刷题 -- 第五届蓝桥杯

题头：本内容所有题面都来自博客：https://blog.csdn.net/ryo_218/article/details/79704030在此感谢！

1、标题：啤酒和饮料
啤酒每罐2.3元，饮料每罐1.9元。小明买了若干啤酒和饮料，一共花了82.3元。
我们还知道他买的啤酒比饮料的数量少，请你计算他买了几罐啤酒。
注意：答案是一个整数。请通过浏览器提交答案。

不要书写任何多余的内容（例如：写了饮料的数量，添加说明文字等）。

思路：

勉强说是贪心吧。。i从1开始，j从i+1开始保证符合题意就好。

#include <iostream>
#include <cstdio>

using namespace std;



int main()
{
    for(int i = 1; i < 100; ++i)
        for(int j = i+1; j < 100; ++j)
            if((23*i+19*j) == 823)
            {
                printf("%d\n", i);
            }
    return 0;
}

View Code

答案是 11

2、标题：切面条
一根高筋拉面，中间切一刀，可以得到2根面条。
如果先对折1次，中间切一刀，可以得到3根面条。
如果连续对折2次，中间切一刀，可以得到5根面条。
那么，连续对折10次，中间切一刀，会得到多少面条呢？

答案是个整数，请通过浏览器提交答案。不要填写任何多余的内容。

画画图就知道(最好用纸条试一下)

除了第一个后均为2^(n-1)+1

答案是 1025

3、

标题：李白打酒
话说大诗人李白，一生好饮。幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。
请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。
注意：通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。

思路：

简单DFS，注意的是要明确什么时候结束，这个是在wine == 1并且还剩下一个可以填的时候（最后一个是b！）结束。否则退出。

下面是AC代码：

#include <iostream>
#include <cstdio>

using namespace std;
int ans = 0;

void dfs(int n, int store, int flower, int wine)
{
    if(store > 5 || flower > 9 || wine < 0) return;
    if(n == 1)
    {
        if(wine == 1)
        {
            ans++;
            return;
        }
        else return;
    }
    dfs(n-1, store+1, flower, wine*2);
    dfs(n-1, store, flower+1, wine-1);
}

int main()
{
    dfs(15, 0, 0, 2);
    printf("%d", ans);
}

View Code

4、

标题：史丰收速算
史丰收速算法的革命性贡献是：从高位算起，预测进位。不需要九九表，彻底颠覆了传统手算!
速算的核心基础是：1位数乘以多位数的乘法。
其中，乘以7是最复杂的，就以它为例。
因为，1/7 是个循环小数：0.142857...，如果多位数超过 142857...，就要进1
同理，2/7, 3/7, ... 6/7 也都是类似的循环小数，多位数超过 n/7，就要进n
下面的程序模拟了史丰收速算法中乘以7的运算过程。
乘以 7 的个位规律是：偶数乘以2，奇数乘以2再加5，都只取个位。
乘以 7 的进位规律是：
满 142857... 进1,
满 285714... 进2,
满 428571... 进3,
满 571428... 进4,
满 714285... 进5,
满 857142... 进6
请分析程序流程，填写划线部分缺少的代码。

//计算个位 
int ge_wei(int a)
{
    if(a % 2 == 0)
        return (a * 2) % 10;
    else
        return (a * 2 + 5) % 10;    
}
 
//计算进位 
int jin_wei(char* p)
{
    char* level[] = {
        "142857",
        "285714",
        "428571",
        "571428",
        "714285",
        "857142"
    };
    
    char buf[7];
    buf[6] = '\0';
    strncpy(buf,p,6);
    
    int i;
    for(i=5; i>=0; i--){
        int r = strcmp(level[i], buf);
        if(r<0) return i+1;
        while(r==0){
            p += 6;
            strncpy(buf,p,6);
            r = strcmp(level[i], buf);
            if(r<0) return i+1;
            ______________________________;  //填空
        }
    }
    
    return 0;
}
 
//多位数乘以7
void f(char* s) 
{
    int head = jin_wei(s);
    if(head > 0) printf("%d", head);
    
    char* p = s;
    while(*p){
        int a = (*p-'0');
        int x = (ge_wei(a) + jin_wei(p+1)) % 10;
        printf("%d",x);
        p++;
    }
    
    printf("\n");
}
 
int main()
{
    f("428571428571");
    f("34553834937543");        
    return 0;
}

注意：通过浏览器提交答案。只填写缺少的内容，不要填写任何多余的内容（例如：说明性文字）

在这道题我们研究透进位运算就可以了。

可知，lever[i]就是判断进位的那7个数，

strncpy(buf,p,6); 这句话是将原字符前6个读取进去。
所以buf内存的是字符串前6个字符。

而strcmp函数：

设这两个字符串为str1，str2，

若str1=str2，则返回零；

若str1<str2，则返回负数；

若str1>str2，则返回正数。

所以r只有-1， 0， 1三种情况，

所以，当r<0说明str2 > str1 这种情况直接i+1就行。
反之则返回i.

所以，答案就是 if(r>0) return i;

5、

标题：打印图形
小明在X星球的城堡中发现了如下图形和文字：
rank=3
*
* *
* *
* * * *
rank=5
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
ran=6
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
小明开动脑筋，编写了如下的程序，实现该图形的打印。

#define N 70
 
void f(char a[][N], int rank, int row, int col)
{
    if(rank==1){
        a[row][col] = '*';
        return;
    }
    
    int w = 1;
    int i;
    for(i=0; i<rank-1; i++) w *= 2;
    
    ____________________________________________;
    f(a, rank-1, row+w/2, col);
    f(a, rank-1, row+w/2, col+w);
}
 
int main()
{
    char a[N][N];
    int i,j;
    for(i=0;i<N;i++)
    for(j=0;j<N;j++) a[i][j] = ' ';
    
    f(a,6,0,0);
    
    for(i=0; i<N; i++){
        for(j=0; j<N; j++) printf("%c",a[i][j]);
        printf("\n");
    }
    
    return 0;
}

思路：

复制代码，补全一下

然后试一试得到结果：

f(a, rank-1, row, col+w/2);

6、

标题：奇怪的分式
上小学的时候，小明经常自己发明新算法。一次，老师出的题目是：
1/4 乘以 8/5
小明居然把分子拼接在一起，分母拼接在一起，答案是：18/45 （参见图1.png）

老师刚想批评他，转念一想，这个答案凑巧也对啊，真是见鬼！
对于分子、分母都是 1~9 中的一位数的情况，还有哪些算式可以这样计算呢？
请写出所有不同算式的个数（包括题中举例的）。
显然，交换分子分母后，例如：4/1 乘以 5/8 是满足要求的，这算做不同的算式。
但对于分子分母相同的情况，2/2 乘以 3/3 这样的类型太多了，不在计数之列!
注意：答案是个整数（考虑对称性，肯定是偶数）。请通过浏览器提交。不要书写多余的内容。

思路：

模拟一下，注意最好比赛的时候把结果打出来看看

#include <iostream>
#include <cstdio>

using namespace std;

int gcd(int a, int b)
{
    return a%b==0?b:gcd(b, a%b);
}

int main()
{
    int cnt = 0;
    for(int a = 1; a <= 9; ++a)
        for(int b = 1; b <= 9; ++b)
            for(int c = 1; c <= 9; ++c)
                for(int d = 1; d <= 9; ++d)
                    if(a != b && c != d)
                    {
                        int x1 = a*c, x2 = a*10+c;
                        int y1 = b*d, y2 = b*10+d;
                        if(x1 != y1 && x2 != y2)
                        {
                            int n = gcd(x1, y1);
                            x1 /= n; y2 /= n;
                            if(x2%x1 == 0 && y2%y1 == 0)
                            {
                                int x = x2/x1;
                                if(y2%x == 0)
                                {
                                    cnt++;
                                    //printf("%d/%d    %d/%d\n", x1*n, y1*n, x2, y2);
                                }
                            }
                        }
                    }
    printf("%d\n", cnt);
}

View Code

也可以由a/b * c/d = e/f 转化成 a*c*f=b*d*e。

代码：

#include <iostream>
#include <cstdio>

using namespace std;

int gcd(int a, int b)
{
    return a%b==0?b:gcd(b, a%b);
}

int main()
{
    int cnt = 0;
    for(int a = 1; a <= 9; ++a)
        for(int b = 1; b <= 9; ++b)
            for(int c = 1; c <= 9; ++c)
                for(int d = 1; d <= 9; ++d)
                    if(a != b && c != d)
                    {
                        int x1 = a*c, x2 = a*10+c;
                        int y1 = b*d, y2 = b*10+d;
                        if(x1 != y1 && x2 != y2)
                        {
                            if(x1*y2 == y1*x2) cnt++;
                        }
                    }
    printf("%d\n", cnt);
}

View Code

答案是14.

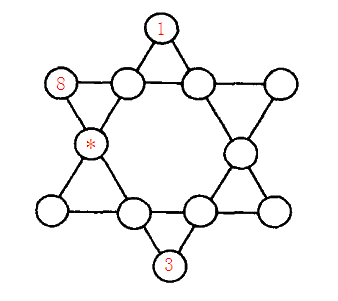
6、标题：六角填数
如图【1.png】所示六角形中，填入1~12的数字。

使得每条直线上的数字之和都相同。

图中，已经替你填好了3个数字，请你计算星号位置所代表的数字是多少？

请通过浏览器提交答案，不要填写多余的内容。

思路

这里用到了STL中求全排列的函数next_permutaiton(array, array+len-1)

关于next_permutation()这个函数这个博客讲的很清楚https://www.cnblogs.com/eudiwffe/p/6260699.html

下面是代码：

#include <iostream>
#include <cstdio>
#include <math.h>
#include <algorithm>

using namespace std;

int main()
{
    int a[9] = {2, 4, 5, 6, 7, 9, 10, 11, 12};
    while(next_permutation(a, a+9))
    {
        int L1 = 1+a[0]+a[3]+a[5];
        int L2 = 1+a[1]+a[4]+a[8];
        int L3 = 8+a[0]+a[1]+a[2];
        int L4 = 8+a[3]+a[6]+3;
        int L5 = 3+a[7]+a[4]+a[2];
        if(L1 == L2 && L2 == L3 && L3 == L4 && L4 == L5)
        {
            printf("%d\n", a[3]);
            break;
        }
    }
}

View Code

答案为10.

8、

标题：蚂蚁感冒
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左，有的朝右。
每只蚂蚁都只能沿着杆子向前爬，速度是1厘米/秒。
当两只蚂蚁碰面时，它们会同时掉头往相反的方向爬行。
这些蚂蚁中，有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时，会把感冒传染给碰到的蚂蚁。
请你计算，当所有蚂蚁都爬离杆子时，有多少只蚂蚁患上了感冒。

【数据格式】
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值，表示蚂蚁离开杆子左边端点的距离。正值表示头朝右，负值表示头朝左，数据中不会出现0值，也不会出现两只蚂蚁占用同一位置。其中，第一个数据代表的蚂蚁感冒了。
要求输出1个整数，表示最后感冒蚂蚁的数目。

例如，输入：
3
5 -2 8
程序应输出：
1

再例如，输入：
5
-10 8 -20 12 25
程序应输出：
3

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。
所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>，不能通过工程设置而省略常用头文件。
提交时，注意选择所期望的编译器类型。

思路：

其实，平常人的思维总是会想到模拟，但是，我们仔细想一想，蚂蚁的速度都是一样的，所以我们优化一下模型

记录一下每只蚂蚁离中心点的距离，两只蚂蚁不用交换，相当于交叉。

也就是说，每只蚂蚁有自己的一条路。

#include <iostream>
#include <cstdio>
#include <math.h>
#include <algorithm>

using namespace std;
const int MX = 1e4+10;
int cnt = 0;

struct ant
{
    int dis;
    int index;
    int flag = 0;
} a[MX];

bool cmp(ant a, ant b)
{
    return a.dis < b.dis;
}

int main()
{
    int ans = 0;
    int tmp = 0, le = 0, ri = 0;
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
    {
        int x;
        scanf("%d", &x);
        a[i].dis = abs(x);
        a[i].index = i;
        a[i].flag = x<0?-1:1;
    }
    sort(a+1, a+n+1, cmp);
    for(int i = 1; i <= n; ++i)
    {
        if(a[i].index == 1)
        {
            tmp = i;
            break;
        }
        if(a[i].flag == 1) le++;
    }
    for(int i = tmp+1; i <= n; ++i)
    {
        if(a[i].flag == -1) ri++;
    }
    if((a[tmp].flag = -1 && le == 0) || a[tmp].flag == 1 && ri == 0) ans = 1;
    else ans = 1+le+ri;
    printf("%d\n", ans);
}

View Code

9、

标题：地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角，出口在右下角。
小明被带到地宫的入口，国王要求他只能向右或向下行走。
走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。
当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。
请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

【数据格式】
输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数，表示正好取k个宝贝的行动方案数。该数字可能很大，输出它对 dp 取模的结果。

例如，输入：
2 2 2
1 2
2 1
程序应该输出：
2

再例如，输入：
2 3 2
1 2 3
2 1 5
程序应该输出：
14

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

思路：记忆化搜索，dfs

#include <iostream>
#include <cstdio>
#include <string.h>
#define ll long long

using namespace std;
const int MX = 50+5;
const int mod = 1000000007;
ll mp[MX][MX], dp[MX][MX][MX][MX];
ll ans = 0;
int n, m, k;

void dfs(int x, int y, int cnt, int val)
{
    if(dp[x][y][cnt][val] != -1) return;
    dp[x][y][cnt][val] = 0;
    if(x==n && y==m && cnt == k)
    {
        dp[x][y][cnt][val] = 1;
        return;
    }
    if(mp[x][y] > val && cnt < k)
    {
        dfs(x, y, cnt+1, mp[x][y]);
        dp[x][y][cnt][val] += dp[x][y][cnt+1][ mp[x][y] ];
        dp[x][y][cnt][val] = dp[x][y][cnt][val]%mod;
    }
    if(x < n)
    {
        dfs(x+1, y, cnt, val);
        dp[x][y][cnt][val] += dp[x+1][y][cnt][val];
        dp[x][y][cnt][val] = dp[x][y][cnt][val]%mod;
    }
    if(y < m)
    {
        dfs(x, y+1, cnt, val);
        dp[x][y][cnt][val] += dp[x][y+1][cnt][val];
        dp[x][y][cnt][val] = dp[x][y][cnt][val]%mod;
    }
    return;
}

int main()
{
    memset(dp, -1, sizeof(dp));
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
        {
            scanf("%lld", &mp[i][j]);
            mp[i][j]++;
        }
    dfs(1, 1, 0, 0);
    printf("%lld\n", dp[1][1][0][0]);

}

View Code

10,

标题：小朋友排队
n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列，但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候，所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换，则他的不高兴程度增加1，如果第二次要求他交换，则他的不高兴程度增加2（即不高兴程度为3），依次类推。当要求某个小朋友第k次交换时，他的不高兴程度增加k。
请问，要让所有小朋友按从低到高排队，他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样，则他们谁站在谁前面是没有关系的。

【数据格式】
输入的第一行包含一个整数n，表示小朋友的个数。
第二行包含 n 个整数 H1 H2 … Hn，分别表示每个小朋友的身高。
输出一行，包含一个整数，表示小朋友的不高兴程度和的最小值。

例如，输入：
3
3 2 1
程序应该输出：
9

【样例说明】
首先交换身高为3和2的小朋友，再交换身高为3和1的小朋友，再交换身高为2和1的小朋友，每个小朋友的不高兴程度都是3，总和为9。

【数据规模与约定】
对于10%的数据， 1<=n<=10；
对于30%的数据， 1<=n<=1000；
对于50%的数据， 1<=n<=10000；
对于100%的数据，1<=n<=100000，0<=Hi<=1000000。

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

posted @ 2019-02-23 17:18 mpeter 阅读(582) 评论(0) 编辑收藏举报

刷新页面返回顶部

Peter

化繁为简大巧不工

蓝桥杯刷题 -- 第五届蓝桥杯

公告

Peter

化繁为简 大巧不工

蓝桥杯刷题 -- 第五届蓝桥杯

公告

化繁为简大巧不工