【基本数据结构之'图'】
基本定义:
在一个社交网络中,每个帐号和他们之间的关系构成了一张巨大的网络,就像下面这张图:

图(graph)是用线连接在一起的顶点或节点的集合,即两个要素:边和顶点。每一条边连接个两个顶点,用(i,j)表示顶点为 i 和 j 的边。
如果用图示来表示一个图,一般用圆圈表示顶点,线段表示边。有方向的边称为有向边,对应的图成为有向图,没有方向的边称为无向边,对应的图叫无向图。对于无向图,边(i, j)和(j,i)是一样的,称顶点 i 和 j 是邻接的,边(i,j)关联于顶点 i 和 j ;对于有向图,边(i,j)表示由顶点 i 指向顶点 j 的边,即称顶点 i 邻接至顶点 j ,顶点 i 邻接于顶点 j ,边(i,j)关联至顶点 j 而关联于顶点 i 。
对于很多的实际问题,不同顶点之间的边的权值(长度、重量、成本、价值等实际意义)是不一样的,所以这样的图被称为加权图,反之边没有权值的图称为无权图。所以,图分为四种:加权有向图,加权无向图,无权有向图,无权无向图。
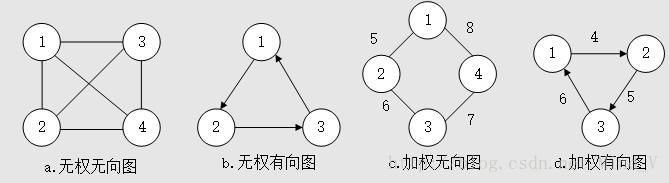
怎么理解有向边和无向边呢?
就拿我们社交软件中的“好友”功能为例。假设有A和B两个用户。
如果只是A关注了B,而B没有关注A,即这是一种单向的关系:只能从A到B,不能从B到A,我们就将这种关系(这条边)称为有向边。
如果A关注了B,B也关注了A,即这是一种双向的关系:可以从A到B,也可以从B到A,我们就把这种关系(这条边)称为无向边。其实,无向边也可以理解为两条有向边,但是在加权的情况下它们的权值是相同的。
相关概念:
在一个无向图中,与一个顶点相关联的边数成为该顶点的度。而对于有向图,则用入度来表示关联至该顶点的边数,出度来表示关联于该顶点的边数。
一个具有n个顶点和n(n-1)/2条边的无向图称为一个完全图,即每个顶点的度等于总顶点数减1。
重要性质:
在无向图或有向图中,顶点的度数总和为边数的两倍,即:
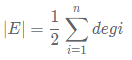
而在有向图中,有一个很明显的性质就是,入度等于出度。
代码实现
下面主要讲解如何用邻接矩阵(二维数组)存图的代码部分。
0.首先定义一个二维数组G
1.初始化
memset(G,0,sizeof(G));
2.插入边
如果是从u到v的无向边:G[u][v]=1,G[v][u]=1;
如果是从u到v的有向边:G[u][v]=1;
3.访问边
如果G[u][v]==1,那么有就有条从u到v的边,否则没有。
4.加权图存法
直接把G数组开成int类型,然后把上面的1改成对应权值即可。
*5.邻接表存图:
邻接表的思想是,对于图中的每一个顶点,用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加,所以对于每个点,我们需要用 vector 来记录。也就是对于每个点,我们都用一个 vector 来记录这个点和哪些点相连。比如对于一张有10个点的图,只要用vector< int > G[10+1] 就可以用来记录这张图了。对于一条从 a 到 b 的有向边,我们通过 G[a].push_back(b) 就可以把这条边添加进去
p.s.如果是无向边,则需要在 G[a].push_back(b)的同时G[b].push_back(a)。
效果如下图:
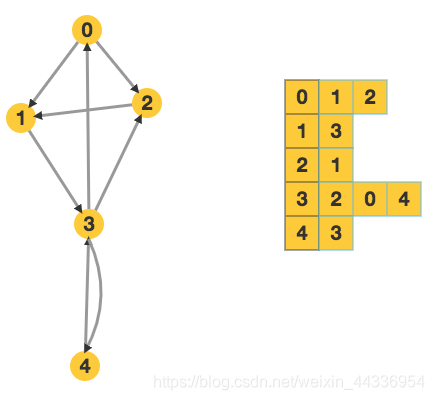
邻接矩阵和邻接表对比
用邻接表存图有两个优点。
- 节省空间:当图的顶点数很多、但是边的数量很少时,如果用邻接矩阵,我们就需要开一个很大的
二维数组,最后我们需要存储 个数。但是用邻接表,最后我们存储的数据量只是边数的两倍。 - 可以记录重复边:如果两个点之间有多条边,用邻接矩阵只能记录一条,但是用邻接表就能记录多条。虽然重复的边看起来是多余的,但在很多时候对解题来说是必要的。
当然,有优点就有缺点,用邻接表存图的最大缺点就是随机访问效率低。比如,我们需要询问点a是否和点b相连,我们就要遍历 G[a]检查这个 vector 里是否有b。而在邻接矩阵中,只需要根据 G[a][b] 就能判断。
因此,我们需要对不同的应用情景选择不同的存图方法。如果是稀疏图(顶点很多、边很少),一般用邻接表;如果是稠密图(顶点很少、边很多),一般用邻接矩阵。
今天先讲到这里,以后会继续更新~
ov.

