力扣 287. 寻找重复数
力扣283. 查找重复数
-
如果不考虑O(1)的额外空间，使用Map查找重复数十分简单
-
使用双指针。首先考虑以下两种情况：
-
如果数组中没有重复的数，以数组
[1,3,4,2]为例，我们将数组下标n和数nums[n]建立一个映射关系 f(n)f(n)，其映射关系
n->f(n)为：0->1
1->3
2->4
3->2我们从下标为 0 出发，根据 f(n)f(n) 计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推，直到下标超界。这样可以产生一个类似链表一样的序列。
0->1->3->2->4->null -
如果数组中有重复的数，以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n)，
其映射关系 n->f(n) 为：
0->1
1->3
2->4
3->2
4->2
同样的，我们从下标为 0 出发，根据 f(n)f(n) 计算出一个值，以这个值为新的下标，再用这个函数计算，以此类推产生一个类似链表一样的序列。这里
2->4是一个循环，那么这个链表可以抽象为下图：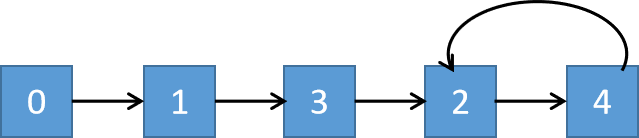
-
因此，可将查找重复数 转化为 查找环形链表的入口。
由于环形链表的存在，使用快慢指针，找到在环中的相遇点：
int slow = 0;
int fast = 0;
slow = nums[slow];
fast = nums[nums[fast]];
while (slow!=fast) {
slow = nums[slow];
fast = nums[nums[fast]];
}
假设环长为 LL，从起点到环的入口的步数是 aa，从环的入口继续走 bb 步到达相遇位置，从相遇位置继续走 cc 步回到环的入口， 则有 b+c=Lb+c=L，其中 LL、aa、bb、cc 都是
正整数。根据上述定义，慢指针走了 a+ba+b 步，快指针走了 2(a+b)2(a+b) 步。从另一 个角度考虑，在相遇位置，快指针比慢指针多走了若干圈，因此快指针走的步数还可以表示成
a+b+kLa+b+kL，其中 kk 表示快指针在 环上走的圈数。联立等式，可以得到
2(a+b)=a+b+kL
2(a+b)=a+b+kL
解得 a=kL-ba=kL−b，整理可得
a=(k-1)L+(L-b)=(k-1)L+c
a=(k−1)L+(L−b)=(k−1)L+c
因此将慢指针在相遇后移到起点，慢指针移动a步，快指针移动k-1圈再走c步，最后都到达环形入口且相遇。
ps：为什么环形入口处就是答案？
在建立数组下标n和数组nums[n]的映射关系后，其映射结果不会出现重复值。还是以数组[1,2,3,4]举例：
0->1
1->3
2->4
3->2
当出现重复值后，例如数组 [1,3,4,2,2]：
0->1
1->3
2->4
3->2
4->2
由于下标3和4的映射关系都指向了相同的结果，最终导致出现环。
