斗地主[NOIP2015]
题目描述
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下:

输入
第一行包含用空格隔开的2个正整数T,N,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据N行,每行一个非负整数对Ai,Bi,表示一张牌,其中Ai表示牌的数码,Bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
输出
输共T行,每行一个整数,表示打光第T组手牌的最少次数。
样例输入1
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
样例输出1
3
样例说明:共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
样例输入2
1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2
样例输出2
6
数据范围
对于不同的测试点, 我们约定手牌组数T与张数n的规模如下:
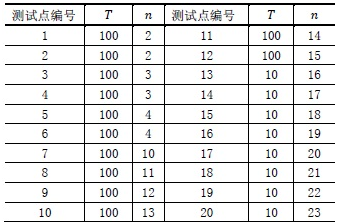
数据保证:所有的手牌都是随机生成的。
时空限制
1024M,2s
【题解】
一道喜闻乐见的大模拟大搜索题,看到了之后就一直跃跃欲试想做一做。考试主要的时间都用来打这道题,刚开始是bfs,卡到直接死机。后来改成dfs,成功过了样例,水过6个点。总觉得dfs不如bfs适合找最优解,但是其实dfs也可以通过剪枝遏制不必要的搜索,而像这种情况非常多的题目bfs要尝试每一种情况的下一步,消耗过大反而不适宜。
正解也是暴搜,但是搜得比我有技巧多了。尽量先打出较多牌来剪枝,最后那些没有被各种特效打出去的牌就直接一视同仁st++就好了。在考试代码上加了最后这条优化瞬间从TLE变成AC,其实想想打单种牌这么简单的事,一句话就解决了何必再来一层dfs呢~据说这道题体现了用各种条件层层剪枝的重要性,但是对于我来说,还是对所谓的“高明的处理方法”更有体会吧。

#include<iostream> #include<cstdio> #include<cstring> using namespace std; int t,n,p[20],a1,a2,jg; bool qk; void init() { memset(p,0,sizeof(p)); for(int i=1;i<=n;i++) { scanf("%d%d",&a1,&a2); if(a1==1) p[12]++; if(a1==2) p[13]++; if(a1>2) p[a1-2]++; if(!a1) { if(a2==1) p[14]++; if(a2==2) p[15]++; } } } void dfs(int st) { if(st>=jg) return; qk=1; int ss,sz,sf; ss=sz=sf=0; for(int i=1;i<=15;i++) { if(p[i]) qk=0; if(p[i]>=2) sz++; if(p[i]>=3) ss++; if(p[i]>=4) sf++; } if(qk) { jg=st; return; } if(st==jg-1) return; int temp; temp=0; for(int i=temp+1;i<=8;i++) if(p[i]) { temp=i; for(int j=i+1;j<=12;j++) { if(p[j]) temp=j; else break; } if(temp>=i+4) { for(int j=i;j<=temp;j++) p[j]--; st++; dfs(st); for(int j=i;j<=temp;j++) p[j]++; st--; } temp++; } if(sz>=3) { temp=0; for(int i=temp+1;i<=10;i++) if(p[i]>=2) { temp=i; for(int j=i+1;j<=12;j++) { if(p[j]>=2) temp=j; else break; } if(temp>=i+2) { for(int j=i;j<=temp;j++) p[j]-=2; st++; dfs(st); for(int j=i;j<=temp;j++) p[j]+=2; st--; } if(temp-i+1==sz) break; temp++; } } if(ss>=2) { temp=0; for(int i=temp+1;i<=11;i++) if(p[i]>=3) { temp=i; for(int j=i+1;j<=12;j++) { if(p[j]>=3) temp=j; else break; } if(temp>=i+1) { for(int j=i;j<=temp;j++) p[j]-=3; st++; dfs(st); for(int j=i;j<=temp;j++) p[j]+=3; st--; } if(temp-i+1==ss) break; temp++; } } if(sf) for(int i=1;i<=15;i++) if(p[i]>=4) { p[i]-=4,st++; for(int j=1;j<=15;j++) if(p[j]) { p[j]--; for(int jk=j;jk<=15;jk++) if(p[jk]) { p[jk]--; dfs(st); p[jk]++; } p[j]++; } if(sz>=2) { for(int j=1;j<=15;j++) if(p[j]>=2) { p[j]-=2; for(int jk=j;jk<=15;jk++) if(p[jk]>=2) { p[jk]-=2; dfs(st); p[jk]+=2; } p[j]+=2; } } p[i]+=4; st--; if(sf==1) break; } if(ss) for(int i=1;i<=15;i++) if(p[i]>=3) { p[i]-=3,st++; for(int j=1;j<=15;j++) if(p[j]&&j!=i) { p[j]--; dfs(st); p[j]++; } if(sz) for(int j=1;j<=15;j++) if(p[j]>=2) { p[j]-=2; dfs(st); p[j]+=2; } p[i]+=3,st--; if(ss==1) break; } if(p[14]&&p[15]) { p[14]--,p[15]--,st++; dfs(st); p[14]++,p[15]++,st--; } for(int i=1;i<=15;i++) if(p[i]) st++; if(st<jg) jg=st; } int main() { scanf("%d%d",&t,&n); for(int l=1;l<=t;l++) { init(); jg=0x3fff; dfs(0); printf("%d\n",jg); } return 0; }



