Password
Description
Rivest是密码学专家。近日他正在研究一种数列E = {E[1],E[2],……,E[n]},
且E[1] = E[2] = p(p为一个质数),E[i] = E[i-2]*E[i-1] (若2<i<=n)。
例如{2,2,4,8,32,256,8192,……}就是p = 2的数列。在此基础上他又设计了一种加密算法,该算法可以通过一个密钥q (q < p)将一个正整数n加密成另外一个正整数d,计算公式为:d = E[n] mod q。现在Rivest想对一组数据进行加密,但他对程序设计不太感兴趣,请你帮助他设计一个数据加密程序。
Input
第一行读入m,p。其中m表示数据个数,p用来生成数列E。 以下有m行,每行有2个整数n,q。n为待加密数据,q为密钥。 数据范围: 0 < p n< 2^31 0 < q < p 0 < m <= 5000。
Output
将加密后的数据按顺序输出到文件 第i行输出第i个加密后的数据。 输入样例1 2 7 4 5 4 6 输入样例2 4 7 2 4 7 1 6 5 9 3
Sample Input
输入样例1
2 7
4 5
4 6
输入样例2
4 7
2 4
7 1
6 5
9 3
Sample Output
输出样例1
3
1
输出样例2
3
0
1
1
时空限制
1s,64MB
【题解】
我心中的题目难度排名:数学>玄学>信息学……千古难题数学题,考试的时候刚开始连式子都没推,直接暴力递推骗来49分。后来一直在打大模拟,最后临交卷回来看一眼好像是斐波那契,起码应该拿矩阵快速幂和普通快速幂搞一搞,但是没有时间了就没有打。
欧拉定理,我的理解就是用来降幂,不过这道题好像模了phi[c]之后并没有加phi[c],此等天机本蒟蒻不明觉厉。这个式子推一推就发现p的指数是斐波那契数列,但是斐波那契数列增长很快,所以只能用欧拉定理降幂。具体做法是预处理或直接求q的欧拉函数,把它作为求斐波那契数列的矩阵快速幂里的模数,然后得到降幂后的指数再普通快速幂求p的幂。
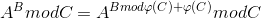
结合快速幂和欧拉定理,这道题大概并不太难。但是在考场上一是没有仔细想,二来也根本没有降幂的意识。数论就像英语音标一样,学了一遍又一遍,还是忘的多会的少。改题的过程更痛苦,几乎是重学欧拉函数(欧拉定理我学过吗?),原来学的数论只为了做那么两三道题,过后连点定义都说不明白。提高数学水平,是迫在眉睫的问题了。

#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #define ll long long using namespace std; const int sj=1000010; int m; ll n,p,q,temp,k,phi[sj],s[sj],ge; bool v[sj]; void prime(ll x) { for(ll i=2;i<x;i++) { if(!v[i]) { s[ge++]=i; phi[i]=i-1; } for(ll j=0;j<ge&&i*s[j]<x;j++) { ll mb=i*s[j]; v[mb]=1; if(i%s[j]==0) { phi[mb]=phi[i]*s[j]; break; } else phi[mb]=phi[i]*(s[j]-1); } } phi[1]=1; } ll fb(ll x,ll y) { ll a[2][2]={0},ans[2][2]={0},f[2][2]={0}; a[0][0]=a[0][1]=a[1][0]=ans[1][1]=ans[0][0]=1; while(x) { if(x&1) { memset(f,0,sizeof(f)); for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) f[i][j]+=ans[i][l]*a[l][j]%y; memcpy(ans,f,sizeof(f)); } x>>=1; memset(f,0,sizeof(f)); for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) f[i][j]+=a[i][l]*a[l][j]%y; memcpy(f,a,sizeof(a)); } memset(f,0,sizeof(f)); memset(a,0,sizeof(a)); f[0][0]=1; f[1][0]=1; for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int l=0;l<2;l++) a[i][j]+=f[i][l]*ans[l][j]%y; return a[0][0]%y; } ll ph(ll x) { if(x<sj) return phi[x]; ll temp=x; for(ll i=2;i*i<=x;i++) if(x%i==0) { temp=temp-temp/i; while(x%i==0) x/=i; } if(x>1) temp=temp-temp/x; return temp; } ll ksm(ll x,ll y,ll z) { x%=z; ll jg=1; while(y) { if(y&1) jg=jg*x%z; x=x*x%z; y>>=1; } return jg%z; } int main() { prime(sj-1); scanf("%d%lld",&m,&p); for(int i=1;i<=m;i++) { scanf("%lld%lld",&n,&q); printf("%lld\n",ksm(p,fb((n-1),ph(q)),q)); } return 0; }


