聪聪和可可[NOI2005]
【问题描述】
在一个魔法森林里,住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。虽然灰姑娘非常喜欢她们俩,但是,聪聪终究是一只猫,而可可终究是一只老鼠,同样不变的是,聪聪成天想着要吃掉可可。
一天,聪聪意外得到了一台非常有用的机器,据说是叫GPS,对可可能准确的定位。有了这台机器,聪聪要吃可可就易如反掌了。于是,聪聪准备 马上出发,去找可可。而可怜的可可还不知道大难即将临头,仍在森林里无忧无虑的玩耍。小兔子乖乖听到这件事,马上向灰姑娘报告。灰姑娘决定尽快阻止聪聪, 拯救可可,可她不知道还有没有足够的时间。
整个森林可以认为是一个无向图,图中有N个美丽的景点,景点从1至N编号。小动物们都只在景点休息、玩耍。在景点之间有一些路连接。
当聪聪得到GPS时,可可正在景点M(M≤N)处。以后的每个时间单位,可可都会选择去相邻的景点(可能有多个)中的一个或停留在原景点不 动。而去这些地方所发生的概率是相等的。假设有P个景点与景点M相邻,它们分别是景点R、景点S,……景点Q,在时刻T可可处在景点M,则在(T+1)时 刻,可可有1/(P+1)的可能在景点R,有1/(P+1)的可能在景点S,……,有1/(P+1)的可能在景点Q,还有1/(P+1)的可能停在景点 M。
我们知道,聪聪是很聪明的,所以,当她在景点C时,她会选一个更靠近可可的景点,如果这样的景点有多个,她会选一个标号最小的景点。由于聪聪太想吃掉可可了,如果走完第一步以后仍然没吃到可可,她还可以在本段时间内再向可可走近一步。
在每个时间单位,假设聪聪先走,可可后走。在某一时刻,若聪聪和可可位于同一个景点,则可怜的可可就被吃掉了。灰姑娘想知道,平均情况下,聪聪几步就可能吃到可可。而你需要帮助灰姑娘尽快的找到答案。
【输入文件】
- 从文件中读入数据。
- 数据的第1行为两个整数N和E,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。
- 第2行包含两个整数C和M,以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。
- 接下来E行,每行两个整数,第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。
- 所有的路都是无向的,即:如果能从A走到B,就可以从B走到A。
- 输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。
【输出文件】
- 输出到文件中。
- 输出1个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉。
【样例输入1】
4 3
1 4
1 2
2 3
3 4
【样例输出1】
1.500
【样例说明1】
开始时,聪聪和可可分别在景点1和景点4。
第一个时刻,聪聪先走,她向更靠近可可(景点4)的景点走动,走到景点2,然后走到景点3;假定忽略走路所花时间。
可可后走,有两种可能:
第一种是走到景点3,这样聪聪和可可到达同一个景点,可可被吃掉,步数为1,概率为 0.5。 第二种是停在景点4,不被吃掉。概率为 0.5。
到第二个时刻,聪聪向更靠近可可(景点4)的景点走动,只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。
所以平均的步数是1* 0.5+2* 0.5=1.5步。
【样例输入2】
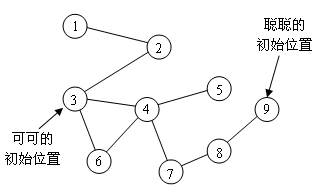
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
【样例输出2】
2.167
【样例说明2】
【数据范围】
- 对于所有的数据,1≤N,E≤980。
- 对于50%的数据,1≤N≤50。
【题解】
第一道概率期望DP(或者说记忆化搜索?),这种有值就返回的操作好像在树形DP那里有些印象。刚开始盯着题面好久,觉得步骤、先后手、两次、字典序这些东西太乱了,完全想不到应该怎么处理,没有一点头绪。后来膜了zzh大佬的题解,才明白这种诡异的问题就应该预处理掉,否则一边dp一边考虑这些条件肯定没法做。1000的数据范围spfa轻轻松松就跑过了,用pr[i][j]表示从i到j猫会选择的点(可以注意到这只猫的行为是非常有逻辑的,就像昨天《幸福的道路》里一定要走最长路一样),用多源改造版spfa跑出来。刚开始学板子的时候总觉得板子的每一步神圣不可侵犯,但是渐渐发现更需要的是在板子的基础上灵活变通,来适应各种题目的需要,比如这道题的简单路径记录,又比如用并查集维护附加信息,这种题目正在渐渐走进我们的视野。
预处理之后就是记忆化搜索,f[i][j]表示从i到j步数的期望,temp实际上是一个走上这条路的概率。用概率乘上不同步骤的期望,加和得到总期望。如果这一步没有成功,老鼠也会继续移动或停止,转移时要注意这一点。刚开始看到zzh代码里有个1.0,没当回事,后来居然发现用1过不了样例!这种弱智问题到现在还在犯,真是太不应该了。具体步骤见代码。
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; const int sj=1010; int n,m,st,fi,h[sj],pr[sj][sj],a1,a2,e,cd[sj]; double f[sj][sj]; struct B { int ne,v; }b[sj*2]; void add(int x,int y) { b[e].v=y; b[e].ne=h[x]; h[x]=e++; } queue<int> q; int dis[sj],ad; bool r[sj]; void spfa(int x) { r[x]=1; dis[x]=0; pr[x][x]=x; q.push(x); while(!q.empty()) { ad=q.front(); for(int i=h[ad];i!=-1;i=b[i].ne) { if(dis[b[i].v]>dis[ad]+1) { dis[b[i].v]=dis[ad]+1; if(!r[b[i].v]) { r[b[i].v]=1; q.push(b[i].v); if(ad==x) pr[x][b[i].v]=b[i].v; else pr[x][b[i].v]=pr[x][ad]; } } if(dis[b[i].v]==dis[ad]+1&&pr[x][b[i].v]>pr[x][ad]) { if(ad==x) pr[x][b[i].v]=b[i].v; else pr[x][b[i].v]=pr[x][ad]; } } q.pop(); r[ad]=0; } } void init() { scanf("%d%d%d%d",&n,&m,&st,&fi); memset(h,-1,sizeof(h)); for(int i=1;i<=m;i++) { scanf("%d%d",&a1,&a2); add(a1,a2); cd[a1]++; add(a2,a1); cd[a2]++; } for(int i=1;i<=n;i++) { memset(dis,0x3f,sizeof(dis)); spfa(i); } } double dp(int x,int y) { if(x==y) return f[x][y]=0; int lb=pr[pr[x][y]][y]; if(pr[x][y]==y||lb==y) return f[x][y]=1; if(f[x][y]) return f[x][y]; double temp=1.0/(cd[y]+1); f[x][y]=temp*dp(lb,y)+1; for(int i=h[y];i!=-1;i=b[i].ne) f[x][y]+=temp*dp(lb,b[i].v); return f[x][y]; } int main() { init(); printf("%.3lf",dp(st,fi)); return 0; }
小学期集训就这么结束了,考试总评rank12。day1一般,day2简直没有分,day3day4勉强追回来一些。只A掉了一道题,打得差不多的有4、5道,至于其他题我立志要拿到的暴力分基本上都拿到了,但是完全没思路的题也有不少。其他时间主要是在改题,只有今天做了一些概率的题,而且做得很困难。以Treap为代表的平衡树只学了点原理,连板子题都没打过。前面的题库AC自动机、树链剖分和dp专题还差不少,状压最后的三道神题一道都没有过。就我个人来说想去打一打更复杂的有附加信息的并查集,还想见识见识大模拟、大搜索。之后是痛苦万分无聊透顶的文化课集训,对于二调(或者说小学期期末)并没有什么想法,但是万一考完要回唐山就得重视点了。文化课那边也不过是那么学,用心第一,用时间倒不是最重要的。相比之下,我更想学学数学数论方面的知识。学文化课简单却痛苦,学奥赛困难却快乐,可是无论如何都得学。希望奥赛集训快点来吧。


