作业要求：
1）贴上视频学习笔记，要求真实，不要抄袭，可以手写拍照。
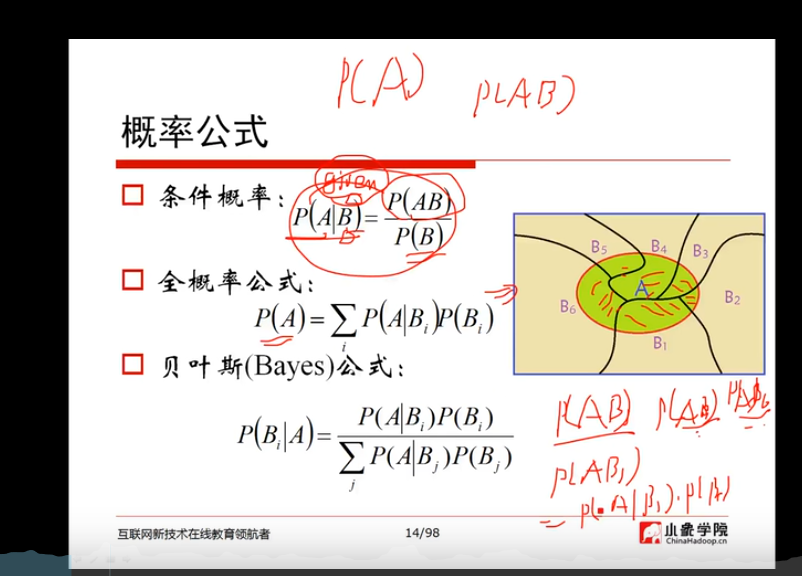
贝叶斯：
泊松分布：
均匀分布;
指数分布：
正态分布：
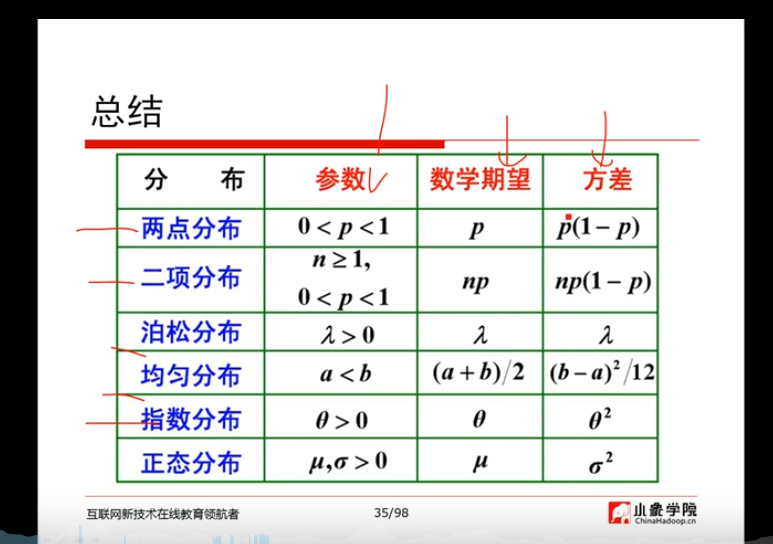
分布总结:
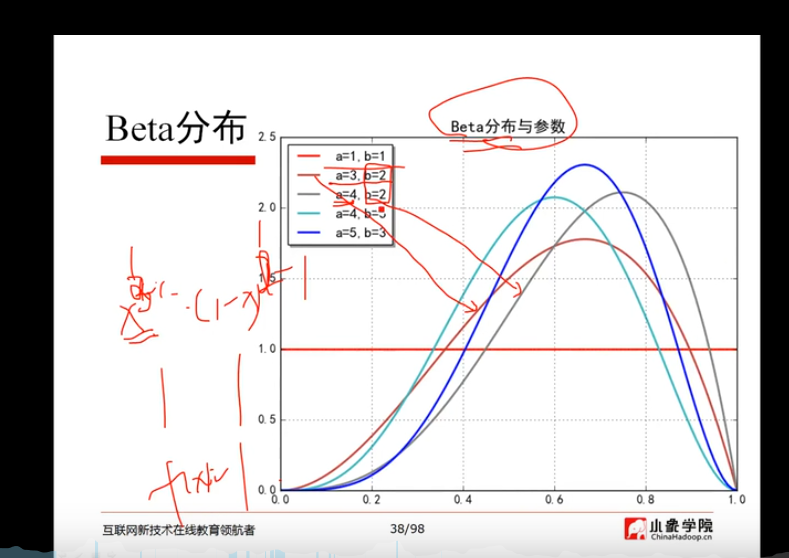
beta分布：
事件的独立性：
期望:
方差：
协方差;
2）用自己的话总结“梯度”，“梯度下降”和“贝叶斯定理”，可以word编辑，可做思维导图，可以手写拍照，要求言简意赅、排版整洁。
梯度：
梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
梯度下降：
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。
贝叶斯定理：
贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。
翻译 朗读 复制 正在查询，请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译（国内） 译
