十一次作业——LL(1)文法的判断,递归下降分析程序
1. 文法 G(S):
(1)S -> AB
(2)A ->Da|ε
(3)B -> cC
(4)C -> aADC |ε
(5)D -> b|ε
验证文法 G(S)是不是 LL(1)文法?
解:
FIRST集:
FIRST(Da)={b,a}
FIRST(ε)={ε}
FIRST(aADC)={a}
FIRST(b)={b}
FOLLOW集:
FOLLOW(A)=FIRST(B)+FIRST(B)+FIRST(B)+FOLLOW(C)={c,a,b,#}
FOLLOW(C)={#}
FOLLOW(D)={a,#}
SELECT集:
SELECT(A->Da)={b,a}
SELECT(A->ε)={c,b,a,#}
SELECT(C->aADC)={a}
SELECT(C->ε)={#}
SELECT(D->b)={b}
SELECT(D->ε)={a,#}
因为:
SELECT(A->Da)∩SELECT(A->ε)≠∅
所以此文法不为LL(1)文法。
2.法消除左递归之后的表达式文法是否是LL(1)文法?
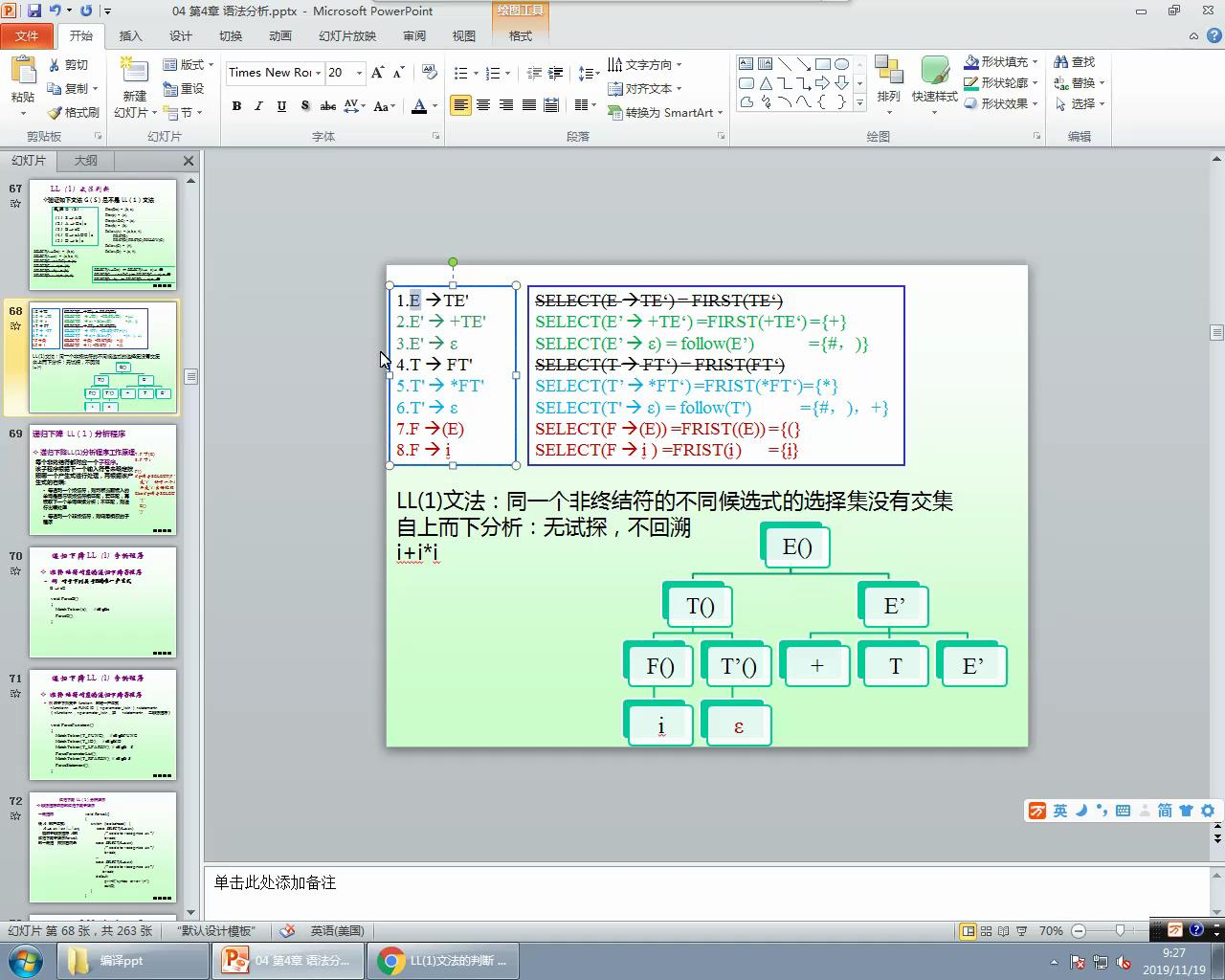
答:是LL(1)文法。
3.接2,如果是LL(1)文法,写出它的递归下降语法分析程序代码。
E()
{T();
E'();
}
E'()
T()
T'()
F()
答:
void ParseE(){
ParseT();
ParseE'();
}
void ParseT() {
ParseF();
ParseT'();
}
void ParseE'() {
switch(lookahead):
case +:
MatchToken(+);
ParseT();
ParseE'();
break;
case #:
break;
case ):
break;
default:
printf('synax error!\n');
exit(0);
}
void ParseF() {
switch(lookahead):
case (:
MatchToken(();
ParseE();
MatchToken());
break;
case i:
MatchToken(i);
break;
default:
printf('synax error!\n');
exit(0);
}
void ParseT'()
{
switch(lookahead):
case *:
ParseF();
MatchToken(*);
ParseT'();
break;
case #:
break;
case ):
break;
case +:
break;
default:
printf('synax error!\n');
exit(0);
}
4.加上实验一的词法分析程序,形成可运行的语法分析程序,分析任意输入的符号串是不是合法的表达式。



