Dijkstra 算法求最短路径

 

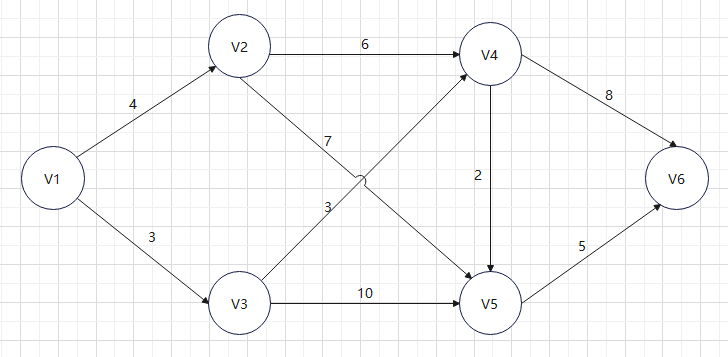
 以上是一个有向无环图，从V1到V2所花费的代价是2，从V1到V3的代价是3，...，以此类推，求出从V1到其他各个点的最短路径。

Dijkstra思路：

1. 建立两个容器，容器S中装着已经求出最短路径的顶点，初始时只有V1，另外一个容器U装着V1到其他顶点的代价，初始时都为无穷大。
   
   
2. 在图中遍历与V1直接相连的顶点V2和V3，发现(V1,V3)=3是最小的，此时将V3加入容器S，并且将V3移出U，得 S={V1=0，V3=3}，U={V2=4，V4=∞，V5=∞，V6=∞}
   
   
3. 以V3为中点，更新U中的其他点到V1的距离，取最小值。如 (V1,V3) + (V3,V4) = 3+3 = 6 < U[V4]=∞，所以U[V4]=6，依次类推，U[V5]=13，的U={V2=4，V4=6，V5=13，V6=∞}
   
   
4. 找出U中最小的值，U[V2]=4，将V2加入到容器S中，并从U中移出，得 S={V1=0，V3=3，V2=4}，U={V4=6，V5=13，V6=∞}
   
   
5. 以V2为中点，更新U中的值，发现V4不用更新，因为(V1,V2)+(V2,V4)=10 < U[V4]=6，但是要更新V5，因为(V1,V2)+(V2,V5)=11 < U[V5]=13，得U={V4=6，V5=11，V6=∞}
   
   
6. 找出U中最小的值，U[V4]=6，将V4加入到容器S中，并从U中移出，S={V1=0，V3=3，V2=4，V4=6}， U={V5=11，V6=∞}
   
   
7. 以V4为中点，更新U中的值，发现(V1,V4)+(V4+V5)=6+2=8 < U[V5]=11，需要更新V5，此外，(V1,V4)+(V4,V6)=6+8=14 < U[V6]=∞ 也需要更新V6, 得出，U={V5=8，V6=14}
   
   
8. 从U中找到最小值，U[V5]=8，将V5加入到容器S中，并从U中移出，得S={V1=0，V3=3，V2=4，V4=6，V5=8}，U={V6=14}
   
   
9. 以V5为中心，更新U中的值，发现(V1,V5)+(V5,V6)=8+5=13 < U[V6]=14，所以更新U={V6=13}
   
   
10. 将剩下的V6加入到容器S中，遍历结束。此时，容器S中就是从V1到各个顶点的最小值。

 以上的4~5、5~6、7~8 都是重复的行为，因为总结出遍历规律：

if (V1,Vx) + (Vx, Vy) < U[Vy]

　　U[Vy] = (V1,Vx) + (Vx,Vy)

这也是Dijkstra的核心思想。

时间复杂度

Dijkstra 算法的时间花费主要体现在重复的4~5步骤中，也就是不断的遍历顶点和边数，所有应该为O(V * E) ，近似可以等于O(E^2)

LeetCode试题

743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

 

示例 1：

 

 

 

 

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2
示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1
示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

 

C#实现解题：

        public int NetworkDelayTime(int[][] times, int n, int k)
        {
            int ans = 0;
            int len = n;
            int[] s = new int[n+1];
            s[k] = 0;
            Dictionary<int, int> u = new Dictionary<int, int>();
            
            //初始化U的各个节点为无穷大
            for(int i = 1; i <= n; ++i)
            {
                if (i != k)
                {
                    u.Add(i, Int32.MaxValue);
                }
            }
            
            //找出直接与K相邻的点，并更新U
            for (int i = 0; i < times.Length; ++i)
            {
                var arr = times[i];
                if (arr[0] == k)
                {
                    u[arr[1]] = arr[2];
                }
            }

            len--;

            while (len > 0)
            {
                int minTemp = Int32.MaxValue;
                int index = -1;
                var uIt = u.GetEnumerator();
                while (uIt.MoveNext())
                {//找到U中最小的点
                    if (uIt.Current.Value < minTemp)
                    {
                        minTemp = uIt.Current.Value;
                        index = uIt.Current.Key;
                    }
                }

                if (index <= -1)
                {
                    return -1;
                }

                s[index] = minTemp;
                u.Remove(index);
                if (ans < minTemp)
                {
                    ans = minTemp;
                }

                if (u.Count <= 0)
                {
                    break;
                }
                
                //以index点为中心，更新U中的点的值
                for (int i = 1; i <= n; ++i)
                {
                    for (int j = 0; j < times.Length; ++j)
                    {
                        int[] timeArr = times[j];
                        if (timeArr[0] == index && timeArr[1] == i && u.ContainsKey(i) && s[index] + timeArr[2] < u[i])
                        {
                            u[i] = s[index] + timeArr[2];
                        }
                    }
                }

                len--;

            }

            return ans;
        }