一、平面图形的面积

1.直角坐标情形

我们已经知道，由曲线 \(y = f(x) (f(x) \geqslant 0)\) 及直线 \(x = a, x = b (a < b)\) 与 \(x\) 轴所围成的曲边梯形的面积 \(A\) 是定积分

其中被积表达式 \(f(x) \mathrm{d}x\) 就是直角坐标下的面积元素，它表示高为 \(f(x)\) 、底为 \(\mathrm{d}x\) 的一个矩形面积。

应用定积分，不但可以计算曲边梯形的面积，还可以计算一些比较复杂的平面图形的面积。

2.极坐标情形

某些平面图形，用极坐标来计算它们的面积比较方便。

设由曲线 \(\rho = \rho(\theta)\) 及射线 \(\theta = \alpha, \theta = \beta\) 围成一图形（简称为曲边扇形），现在要计算它的面积（如图）。这里，\(\rho(\theta)\) 在 \([\alpha, \beta]\) 上连续，且 \(\rho(\theta) \geqslant 0, 0 < \beta - \alpha \leqslant 2\pi\)。

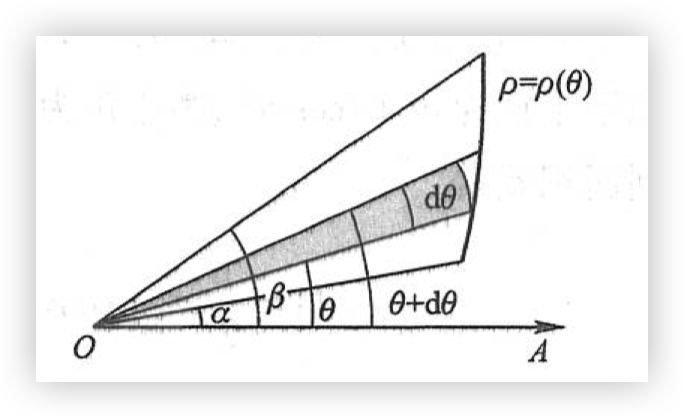
由于当 \(\theta\) 在 \([\alpha, \beta]\) 上变动时，极径 \(\rho = \rho(\theta)\) 也随之变动，因此所求图形面积不能直接利用扇形面积公式 \(A = \cfrac{1}{2} R^2 \theta\) 来计算。

取极角 \(\theta\) 为积分变量，它的变化区间为 \([\alpha, \beta]\) 。相应于任一小区间 \([\theta, \theta + \mathrm{d}\theta]\) 的窄曲边扇形的面积可以用半径为 \(\rho = \rho(\theta)\) 、中心角为 \(\mathrm{d}\theta\) 的扇形的面积来近似代替，从而得到这窄曲边扇形面积的近似值，即曲边扇形的面积元素

以 \(\cfrac{1}{2} [\rho(\theta)]^2 \mathrm{d}\theta\) 为被积表达式，在闭区间 \([\alpha, \beta]\) 上作定积分，便得所求曲边扇形的面积为

二、体积

1.旋转体体积

旋转体就是由一个平面图形绕这平面内一条直线旋转一周而成的立体。这直线叫做旋转轴。圆柱、圆锥、圆台、球可以分别看成是由矩形绕它的一条边、直角三角形绕它的直角边、直角梯形绕它的直角腰、半圆绕它的直径旋转一周而成的立体，所以它们都是旋转体。

上述旋转体都可以看作是由连续曲线 \(y = f(x)\) ，直线 \(x = a, x = b\) 及 \(x\) 轴所围成的曲边梯形绕 \(x\) 轴旋转一周而成的立体。

取横坐标 \(x\) 为积分变量，它的变化区间为 \([a, b]\)。相应于 \([a, b]\) 上的任一小区间 \([x, x + \mathrm{d}x]\) 的窄曲边梯形绕 \(x\) 轴旋转而成的薄片的体积近似于以 \(f(x)\) 为底半径、\(\mathrm{d}x\) 为高的扁圆柱体的体积（如图），即体积元素

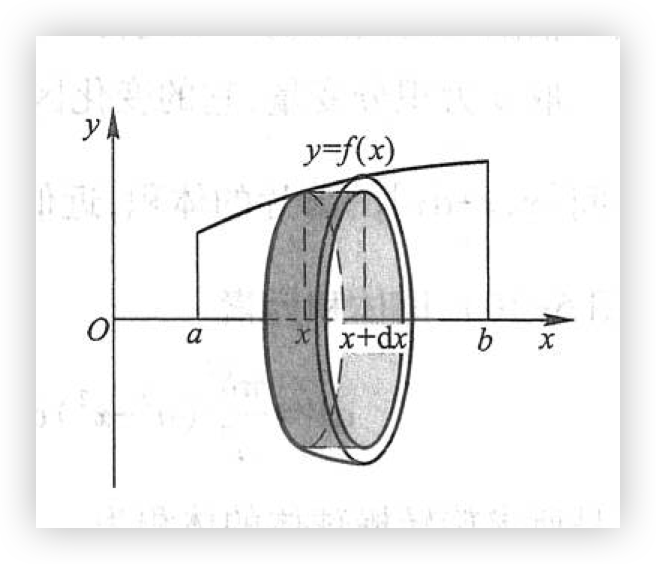
以 \(\pi [f(x)]^2 \mathrm{d}x\) 为被积表达式，在闭区间 \([a, b]\) 上作定积分，便得所求旋转体体积为

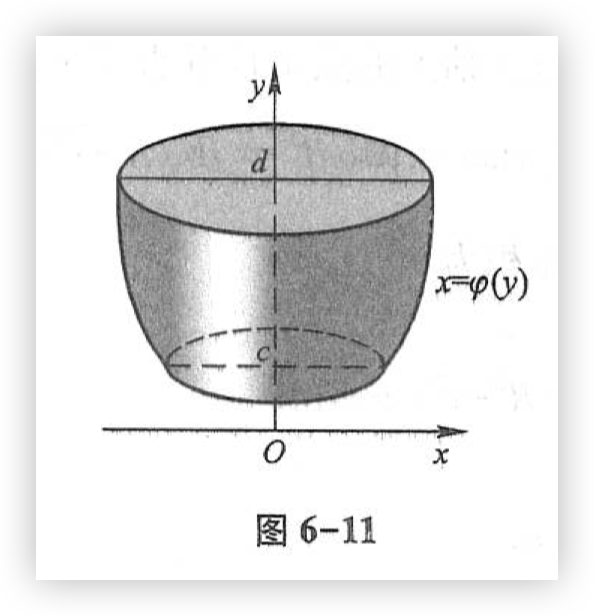
用类似方法可以推出：由曲线 \(x = \varphi(y)\)，直线 \(y = c, y = d (c < d)\) 与 \(y\) 轴所围成的曲边梯形，绕 \(y\) 轴旋转一周而成的旋转体（如图6-11）的体积为

2.平行截面面积为已知的立体的体积

从计算旋转体体积的过程中可以看出：如果一个立体不是旋转体，但却知道该立体上垂直于一定轴的各个截面的面积，那么这个立体的体积也可以用定积分来计算。

如图6-13所示，取上述定轴为 \(x\) 轴，并设该立体在过点 \(x = a, x = b\) 且垂直于 \(x\) 轴的两个平面之间。以 \(A(x)\) 表示过点 \(x\) 且垂直于 \(x\) 轴的截面面积。假定 \(A(x)\) 为已知的 \(x\) 的连续函数。这时，取 \(x\) 为积分变量，它的变化区间为 \([a, b]\) ；立体中相应于 \([a, b]\) 上任一小区间 \([x, x + \mathrm{d}x]\) 的一薄片的体积，近似于底面积为 \(A(x)\) 、高为 \(\mathrm{d}x\) 的扁柱体的体积，即体积元素

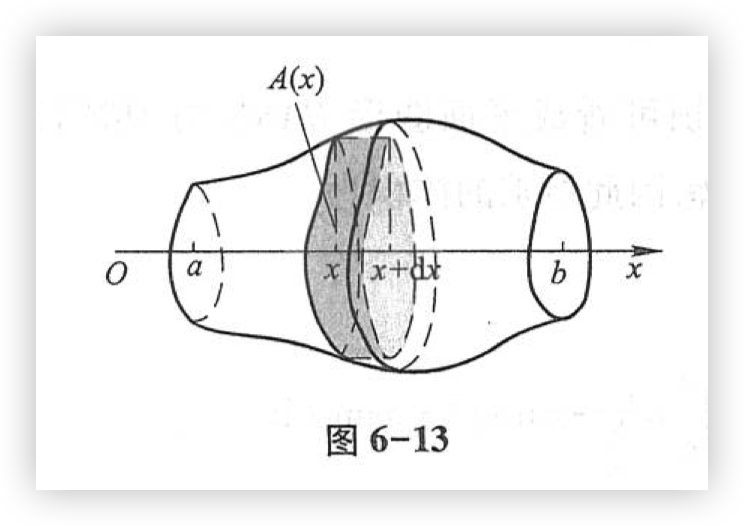
以 \(A(x) \mathrm{d}x\) 为被积表达式，在闭区间 \([a, b]\) 上作定积分，便得所求立体的体积

三、平面曲线的弧长

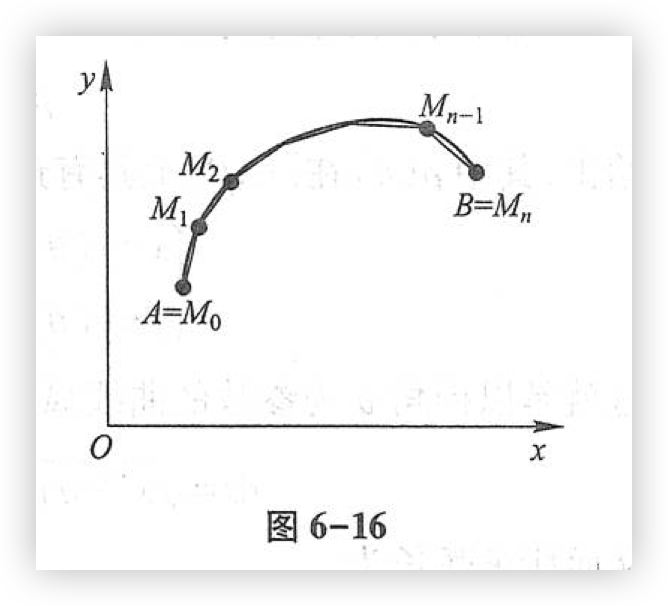
设 \(A, B\) 是曲线弧的两个端点。在弧AB上依次取分点 \(A = M_0, M_1, M_2, \cdots, M_{i - 1}, M_i, \cdots, M_{n - 1}, M_n = B\) ，并依次连接相邻的分点得一折线（图6-16）。当分点的数目无限增加且每个小段弧 \(M_{i - 1} M_i\) 都缩向一点时，如果此时折线的长 \(\displaystyle \sum_{i = 1}^n |M_{i - 1} M_i|\) 的极限存在，那么称此极限为曲线弧AB的弧长，并称此曲线弧AB是可求长的。

对光滑曲线弧有如下结论：

定理 光滑曲线弧是可求长的.

由于光滑曲线弧是可求长的，所以可以用定积分来计算弧长。

设曲线弧由参数方程

给出，其中 \(\varphi(t), \psi(t)\) 在 \([\alpha, \beta]\) 上具有连续导数，且 \(\varphi'(t), \psi'(t)\) 不同时为零。现在来计算这曲线弧段的长度。

取参数 \(t\) 为积分变量，它的变化区间为 \([\alpha, \beta]\) 。相应于 \([\alpha, \beta]\) 上任一小区间 \([t, t + \mathrm{d}t]\) 的小弧段的长度 \(\Delta s\) 近似等于对应的弦的长度 \(\sqrt{(\Delta x)^2 + (\Delta y)^2}\) ，因为

所以 \(\Delta s\) 的近似值（弧微分）即弧长元素为

于是所求弧长为

当曲线弧有直角坐标方程

给出，其中 \(f(x)\) 在 \([a, b]\) 上具有一阶连续导数，这时曲线弧有参数方程

从而所求弧长为

当曲线弧由极坐标方程

给出，其中 \(\rho(\theta)\) 在 \([\alpha, \beta]\) 上具有连续导数，则由直角坐标与极坐标的关系可得

这就是以极角 \(\theta\) 为参数的曲线弧的参数方程。于是，弧长元素为

从而所求弧长为