高等数学 6.1 定积分的元素法

在定积分的应用中，经常采用所谓的元素法。为了说明这种方法，先回顾一下曲边梯形的面积问题。

设 \(f(x)\) 在区间 \([a, b]\) 上连续且 \(f(x) \geqslant 0\) ，求以曲线 \(y = f(x)\) 为曲边、底为 \([a, b]\) 的曲边梯形的面积 \(A\) 。把这个面积 \(A\) 表示为定积分

\[A = \int_a^b f(x) \mathrm{d}x \]

的步骤是

（1）用任意一组分点吧区间 \([a, b]\) 分成长度为 \(\Delta x_i (i = 1, 2, \cdots, n)\) 的 \(n\) 个小区间，相应地把曲边梯形分成 \(n\) 个窄曲边梯形，第 \(i\) 个窄曲边梯形的面积设为 \(\Delta A_i\) ，于是有

\[A = \sum_{i = 1}^n \Delta A_i \]

（2）计算 \(\Delta A_i\) 的近似值

\[\Delta A_i \approx f(\xi_i) \Delta x_i \quad (x_{i - 1} \leqslant \xi_i \leqslant x_i) \]

（3）求和，得 \(A\) 的近似值

\[A \approx \sum_{i = 1}^n f(\xi_i) \Delta x_i \]

（4）求极限，记 \(\lambda = \max{ \{\Delta x_1, \Delta x_2, \cdots, \Delta x_n \} }\) ，得

\[A = \lim_{\lambda \to 0} \sum_{i = 1}^n f(\xi_i) \Delta x_i = \int_a^b f(x) \mathrm{d}x \]

在上述问题中，所求量（即面积 \(A\)）与区间 \([a, b]\) 有关。如果把区间 \([a, b]\) 分成许多部分区间，那么所求量相应地分成许多部分分量（即 \(\Delta A_i\)），而所求量等于所有部分量之和（即 \(\displaystyle A = \sum_{i = 1}^n \Delta A_i\)），这一性质称为所求量对于区间 \([a, b]\) 具有可加性。此外，以 \(f(\xi_i) \Delta x_i\) 近似代替部分量 \(\Delta A_i\) 时，要求它们只相差一个比 \(\Delta x_i\) 高阶的无穷小，以使和式 \(\displaystyle \sum_{i = 1}^n f(\xi_i) \Delta x_i\) 的极限是 \(A\) 的精确值，从而 \(A\) 可以表示成定积分

\[A = \int_a^b f(x) \mathrm{d}x \]

在引出 \(A\) 的积分表达式的四个步骤中，主要的是第二步，这一步是要确定 \(\Delta A_i\) 的近似值 \(f(\xi_i) \Delta x_i\) 使得

\[A = \lim_{\lambda \to 0} \sum_{i = 1}^n f(\xi_i) \Delta x_i = \int_a^b f(x) \mathrm{d}x \]

在实用上，为了简便起见，省略下标 \(i\) ，用 \(\Delta A\) 表示任一小区间 \([x, x + \Delta x]\) 上的窄曲边梯形的面积，这样，

\[A = \sum \Delta A \]

取 \([x, x + \Delta x]\) 的左端点 \(x\) 为 \(\xi\) ，以点 \(x\) 处的函数值 \(f(x)\) 为高、\(\mathrm{d}x\) 为底的矩形的面积 \(f(x) \mathrm{d}x\) 为 \(\Delta A\) 的近似值（途中阴影部分所示），即

\[\Delta A \approx f(x) \mathrm{d}x. \]

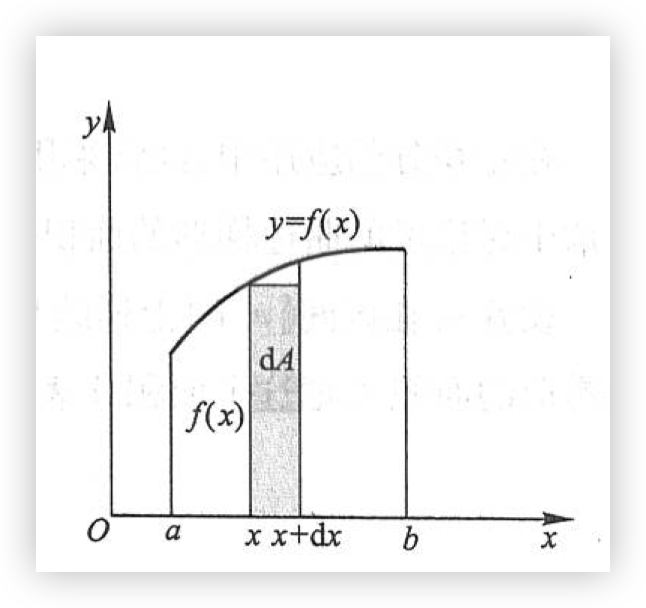
上式右端 \(f(x) \mathrm{d}x\) 叫做面积元素，记为 \(\mathrm{d}A = f(x) \mathrm{d}x\).
于是

\[A \approx \sum f(x) \mathrm{d}x \]

因此

\[A = \lim \sum f(x) \mathrm{d}x = \int_a^b f(x) \mathrm{d}x \]

一般地，如果某一实际问题中的所求量 \(U\) 符合下列条件：

1. \(U\) 是与一个变量 \(x\) 的变化区间 \([a, b]\) 有关的量；
2. \(U\) 对于区间 \([a, b]\) 具有可加性，就是说，如果把区间 \([a, b]\) 分成许多部分区间，那么 \(U\) 相应地分成许多部分量，而 \(U\) 等于所有部分量之和；
3. 部分量 \(U_i\) 的近似值可表示为 \(f(\xi_i) \Delta x\) ，
   那么就可以考虑用定积分来表达这个量 \(U\) 。

通常写出这个量 \(U\) 的积分表达式的步骤是

1. 根据问题的具体情况，选取一个变量例如 \(x\) 为积分变量，并确定它的变化区间 \([a, b]\) ；
2. 设想把区间 \([a, b]\) 分成 \(n\) 个小区间并记作 \([x, x +\mathrm{d}x]\)，求出相应于这个小区间的部分量 \(\Delta U\) 的近似值。如果 \(\Delta U\) 能近似的表示为 \([a, b]\) 上的一个连续函数在 \(x\) 处的值 \(f(x)\) 与 \(\mathrm{d}x\) 的乘积，就把 \(f(x) \mathrm{d}x\) 称为量 \(U\) 的元素且记作 \(\mathrm{d}U\) ，即

\[\mathrm{d}U = f(x) \mathrm{d}x ; \]

3. 以所求量 \(U\) 的元素 \(f(x) \mathrm{d}x\) 为被积表达式，在区间 \([a, b]\) 上做定积分，得

\[U = \int_a^b f(x) \mathrm{d}x \]

这就是所求量 \(U\) 的积分表达式。

这个方法通常叫做元素法。