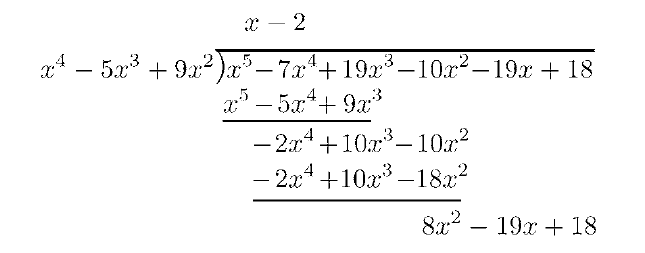1、公式法
使用积分表中的公式可直接求得积分。
(一)含有 \(ax+b\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{ax+b} &= \cfrac{1}{a} \ln \vert ax+1 \vert + C \\
\int (ax + b)^{\mu} \mathrm{d}x &= \cfrac{1}{a(\mu + 1)}(ax + b)^{\mu + 1} + C \\
\int \cfrac{x}{ax + b} \mathrm{d}x &= \cfrac{1}{a^2} (ax + b - b \ln{\vert ax + b \vert}) + C \\
\int \cfrac{x^2}{ax + b} \mathrm{d}x &= \cfrac{1}{a^3} \left[ \cfrac{1}{2} (ax + b)^2 - 2b(ax + b) + b^2 \ln{\vert ax + b \vert} \right] + C \\
\int \cfrac{\mathrm{d}x}{x(ax + b)} &= -\cfrac{1}{b} \ln{\left \vert \cfrac{ax + b}{x} \right \vert} + C \\
\int \cfrac{\mathrm{d}x}{x^2 (ax + b)} &= -\cfrac{1}{bx} + \cfrac{a}{b^2} \ln{\left \vert \cfrac{ax + b}{x} \right \vert} + C \\
\int \cfrac{x}{(ax + b)^2} \mathrm{d}x &= \cfrac{1}{a^2} \left( ln{\lvert ax + b \rvert + \cfrac{b}{ax + b}} \right) + C \\
\int \cfrac{x^2}{(ax + b)^2} \mathrm{d}x &= \cfrac{1}{a^3} \left( ax + b - 2b\ln{\lvert ax + b \rvert} - \cfrac{b^2}{ax + b} \right) + C \\
\int \cfrac{\mathrm{d}x}{x (ax + b)^2} &= \cfrac{1}{b(ax + b)} - \cfrac{1}{b^2} \ln{\left \vert \cfrac{ax + b}{x} \right \vert} + C \\
\end{align}
\]
(二)含有 \(\sqrt{ax + b}\) 的积分
\[\begin{align}
\int \sqrt{ax + b} \, \mathrm{d}x &= \cfrac{2}{3a} \sqrt{(ax + b)^3} + C \\
\int x \sqrt{ax + b} \, \mathrm{d}x &= \cfrac{2}{15 a^2} (3ax - 2b) \sqrt{(ax + b)^3} + C \\
\int x^2 \sqrt{ax + b} \, \mathrm{d}x &= \cfrac{2}{105a^3} (15 a^2 x^2 - 12abx + 8b^2) \sqrt{(ax + b)^3} + C \\
\int \cfrac{x}{\sqrt{ax + b}} \mathrm{d}x &= \cfrac{2}{3a^2} (ax - 2b) \sqrt{ax + b} + C \\
\int \cfrac{x^2}{\sqrt{ax + b}} \mathrm{d}x &= \cfrac{2}{15a^3} (3 a^2 x^2 - 4abx + 8b^2) \sqrt{ax + b} + C \\
\int \cfrac{\mathrm{d}x}{x \sqrt{ax + b}} &=
\begin{cases}
\cfrac{1}{\sqrt{b}} \ln{\left \lvert \cfrac{\sqrt{ax + b} - \sqrt{b}}{\sqrt{ax + b} + \sqrt{b}} \right \rvert} + C& b>0 \\
\cfrac{2}{\sqrt{-b}} \arctan{\sqrt{\cfrac{ax + b}{-b}}} + C& b<0
\end{cases} \\
\int \cfrac{\mathrm{d}x}{x^2 \sqrt{ax + b}} &= -\cfrac{\sqrt{ax + b}}{bx} - \cfrac{a}{2b} \int \cfrac{\mathrm{d}x}{x \sqrt{ax + b}} \\
\int \cfrac{\sqrt{ax + b}}{x} \mathrm{d}x &= 2 \sqrt{ax + b} + b \int \cfrac{\mathrm{d}x}{x \sqrt{ax + b}} \\
\int \cfrac{\sqrt{ax + b}}{x^2} \mathrm{d}x &= - \cfrac{\sqrt{ax + b}}{x} + \cfrac{a}{2} \int \cfrac{\mathrm{d}x}{x \sqrt{ax + b}}
\end{align}
\]
(三)含有 \(x^2 \pm a^2\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{x^2 + a^2} &= \cfrac{1}{a} \arctan{\cfrac{x}{a}} + C \\
\int \cfrac{\mathrm{d}x}{(x^2 + a^2)^n} &= \cfrac{x}{2(n - 1)a^2(x^2 + a^2)^{n - 1}} + \cfrac{2n - 3}{2(n-1)a^2} \int \cfrac{\mathrm{d}x}{(x^2 + a^2)^{n - 1}} \\
\int \cfrac{\mathrm{d}x}{x^2 - a^2} &= \cfrac{1}{2a} \ln{\left \lvert \cfrac{x - a}{x + a} \right \rvert} + C \\
\end{align}
\]
(四)含有 \(ax^2 + b(a > 0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{ax^2 + b} &=
\begin{cases}
\cfrac{1}{\sqrt{ab}}\arctan{\sqrt{\cfrac{a}{b}}x} + C \quad &b>0 \\
\cfrac{1}{2\sqrt{-ab}} \ln{\left \lvert \cfrac{\sqrt{a}x - \sqrt{-b}}{\sqrt{a}x + \sqrt{-b}} \right \rvert} + C \quad &b<0
\end{cases} \\
\int \cfrac{x}{x^2 + b} \mathrm{d}x &= \cfrac{1}{2a} \ln{\vert ax^2 + b \vert} + C \\
\int \cfrac{x^2}{ax^2 + b} \mathrm{d}x &= \cfrac{x}{a} - \cfrac{b}{a} \int \cfrac{\mathrm{d}x}{ax^2 + b} \\
\int \cfrac{\mathrm{d}x}{x(ax^2 + b)} &= \cfrac{1}{2b} \ln{\cfrac{x^2}{\vert ax^2 + b \vert}} + C \\
\int \cfrac{\mathrm{d}x}{x^2(ax^2 + b)} &= -\cfrac{1}{bx} - \cfrac{a}{b} \int \cfrac{\mathrm{d}x}{ax^2 + b} \\
\int \cfrac{\mathrm{d}x}{x^3(ax^2 + b)} &= \cfrac{a}{2b^2} \ln{\cfrac{\lvert ax^2 + b \rvert}{x^2}} - \cfrac{1}{2bx^2} + C \\
\int \cfrac{dx}{(ax^2 + b)^2} &= \cfrac{x}{2b(ax^2 + b)} + \cfrac{1}{2b} \int \cfrac{\mathrm{d}x}{ax^2 + b} \\
\end{align}
\]
(五)含有 \(ax^2 + bx + c (a>0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{ax^2 + bx + c} &=
\begin{cases}
\cfrac{2}{\sqrt{4ac - b^2}} \arctan{\cfrac{2ax + b}{\sqrt{4ac - b^2}}} + C \quad &b^2<4ac \\
\cfrac{1}{\sqrt{b^2 - 4ac}} \ln{\left \lvert \cfrac{2ax + b - \sqrt{b^2 - 4ac}}{2ax + b + \sqrt{b^2 - 4ac}} \right \rvert} + C \quad &b^2>4ac
\end{cases}\\
\int \cfrac{x}{ax^2 + bx + c} \mathrm{d}x &= \cfrac{1}{2a} \ln{\lvert ax^2 + bx + c \rvert} - \cfrac{b}{2a} \int \cfrac{\mathrm{d}x}{ax^2 + bx + c}
\end{align}
\]
(六)含有 \(\sqrt{x^2 + a^2}(a>0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{\sqrt{x^2 + a^2}} &= arsinh\,\cfrac{x}{a} + C_1 = \ln{x + \sqrt{x^2 + a^2}} + C \\
\int \cfrac{\mathrm{d}x}{\sqrt{(x^2 + a^2)^3}} &= \cfrac{x}{a^2 \sqrt{x^2 + a^2}} + C \\
\int \cfrac{x}{\sqrt{x^2 + a^2}} \mathrm{d}x &= \sqrt{x^2 + a^2} + C \\
\int \cfrac{x}{\sqrt{(x^2 + a^2)^3}} \mathrm{d}x &= - \cfrac{1}{\sqrt{x^2 + a^2}} + C \\
\int \cfrac{x^2}{\sqrt{x^2 + a^2}} \mathrm{d}x &= \cfrac{x}{2} \sqrt{x^2 + a^2} - \cfrac{a^2}{2} \ln{(x + \sqrt{x^2 + a^2})} + C \\
\int \cfrac{x^2}{\sqrt{(x^2 + a^2)^3}} \mathrm{d}x &= -\cfrac{x}{\sqrt{x^2 + a^2}} + \ln{(x + \sqrt{x^2 + a^2})} + C \\
\int \cfrac{\mathrm{d}x}{x \sqrt{x^2 + a^2}} &= \cfrac{1}{a} \ln{\cfrac{\sqrt{x^2 + a^2}-a}{\lvert x \rvert}} + C \\
\int \cfrac{\mathrm{d}x}{x^2 \sqrt{x^2 + a^2}} &= - \cfrac{\sqrt{x^2 + a^2}}{a^2x} + C \\
\int \sqrt{x^2 + a^2} \mathrm{d}x &= \cfrac{x}{2} \sqrt{x^2 + a^2} + \cfrac{a^2}{2} \ln{(x + \sqrt{x^2 + a^2})} + C \\
\int \sqrt{(x^2 + a^2)^3} \mathrm{d}x &= \cfrac{x}{8} (2x^2 + 5a^2) \sqrt{x^2 + a^2} + \cfrac{3}{8} a^4 \ln{(x + \sqrt{x^2 + a^2})} + C \\
\int x \sqrt{x^2 + a^2} \mathrm{d}x &= \cfrac{1}{3} \sqrt{(x^2 + a^2)^3} + C \\
\int x^2 \sqrt{x^2 + a^2} \mathrm{d}x &= \cfrac{x}{8} (2x^2 + a^2) \sqrt{x^2 + a^2} - \cfrac{a^4}{8} \ln{(x + \sqrt{x^2 + a^2})} + C \\
\int \cfrac{\sqrt{x^2 + a^2}}{x} \mathrm{d}x &= \sqrt{x^2 + a^2} + a\ln{\cfrac{\sqrt{x^2 + a^2} - a}{\lvert x \rvert}} + C \\
\int \cfrac{\sqrt{x^2 + a^2}}{x^2} \mathrm{d}x &= - \cfrac{\sqrt{x^2 + a^2}}{x} + \ln{(x + \sqrt{x^2 + a^2})} + C
\end{align}
\]
(七)含有 \(\sqrt{x^2 - a^2}(a>0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{\sqrt{x^2 - a^2}} &= \cfrac{x}{\lvert x \rvert}arcosh\, \cfrac{\lvert x \rvert}{a} + C_1 = \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int \cfrac{\mathrm{d}x}{\sqrt{(x^2 - a^2)^3}} &= - \cfrac{x}{a^2 \sqrt{x^2 - a^2}} + C \\
\int \cfrac{x}{\sqrt{x^2 - a^2}} \mathrm{d}x &= \sqrt{x^2 - a^2} + C \\
\int \cfrac{x}{\sqrt{(x^2 - a^2)^3}} \mathrm{d}x &= - \cfrac{1}{\sqrt{(x^2 - a^2)}} + C \\
\int \cfrac{x^2}{\sqrt{x^2 - a^2}} \mathrm{d}x &= \cfrac{x}{2} \sqrt{x^2 - a^2} + \cfrac{a^2}{2} \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int \cfrac{x^2}{\sqrt{(x^2 - a^2)^3}} \mathrm{d}x &= - \cfrac{x}{\sqrt{x^2 - a^2}} + \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int \cfrac{\mathrm{d}x}{x \sqrt{x^2 - a^2}} &= \cfrac{1}{a} \arccos{\cfrac{a}{\lvert x \rvert}} + C \\
\int \cfrac{\mathrm{d}x}{x^2 \sqrt{x^2 - a^2}} &= \cfrac{\sqrt{x^2 - a^2}}{a^2 x} + C \\
\int \sqrt{x^2 - a^2} \mathrm{d}x &= \cfrac{x}{2} \sqrt{x^2 - a^2} - \cfrac{a^2}{2} \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int \sqrt{(x^2 - a^2)^3} \mathrm{d}x &= \cfrac{x}{8} (2x^2 - 5a^2) \sqrt{x^2 - a^2} \cfrac{3}{8} a^4 \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int x \sqrt{x^2 - a^2} \mathrm{d}x &= \cfrac{1}{3} \sqrt{(x^2 - a^2)^3} + C \\
\int x^2 \sqrt{x^2 - a^2} \mathrm{d}x &= \cfrac{x}{8}(2x^2 - a^2) \sqrt{x^2 - a^2} - \cfrac{a^4}{8} \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\int \cfrac{\sqrt{x^2 - a^2}}{x} \mathrm{d}x &= \sqrt{x^2 - a^2} - a \arccos{\cfrac{a}{\lvert x \rvert}} + C \\
\int \cfrac{\sqrt{x^2 - a^2}}{x^2} \mathrm{d}x &= - \cfrac{x^2 - a^2}{x} + \ln{\lvert x + \sqrt{x^2 - a^2} \rvert} + C \\
\end{align}
\]
(八)含有 \(\sqrt{a^2 - x^2}(a>0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{\sqrt{a^2 - x^2}} &= \arcsin{\cfrac{x}{a}} + C \\
\int \cfrac{\mathrm{d}x}{\sqrt{(a^2 - x^2)^3}} &= \cfrac{x}{a^2 \sqrt{a^2 - x^2}} + C \\
\int \cfrac{x}{\sqrt{a^2 - x^2}} \mathrm{d}x &= - \sqrt{a^2 - x^2} + C \\
\int \cfrac{x}{\sqrt{(a^2 - x^2)^3}} \mathrm{d}x &= \cfrac{1}{\sqrt{a^2 - x^2}} + C \\
\int \cfrac{x^2}{\sqrt{a^2 - x^2}} \mathrm{d}x &= -\cfrac{x}{2} \sqrt{a^2 - x^2} + \cfrac{a^2}{2} \arcsin{\cfrac{x}{a}} + C \\
\int \cfrac{x^2}{\sqrt{(a^2 - x^2)^3}} \mathrm{d}x &= \cfrac{x}{\sqrt{a^2 - x^2}} - \arcsin{\cfrac{x}{a}} + C \\
\int \cfrac{\mathrm{d}x}{x \sqrt{a^2 - x^2}} &= \cfrac{1}{a} \ln{\cfrac{a - \sqrt{a^2 - x^2}}{\lvert x \rvert}} + C \\
\int \cfrac{\mathrm{d}x}{x^2 \sqrt{a^2 - x^2}} &= -\cfrac{\sqrt{a^2 - x^2}}{a^2 x} + C \\
\int \sqrt{a^2 - x^2} \mathrm{d}x &= \cfrac{x}{2} \sqrt{a^2 - x^2} + \cfrac{a^2}{2} \arcsin{\cfrac{x}{a}} + C \\
\int \sqrt{(a^2 - x^2)^3} \mathrm{d}x &= \cfrac{x}{8} (5a^2 - 2x^2) \sqrt{a^2 - x^2} + \cfrac{3}{8} a^4 \arcsin{\cfrac{x}{a}} + C \\
\int x \sqrt{a^2 - x^2} \mathrm{d}x &= - \cfrac{1}{3} \sqrt{(a^2 - x^2)^3} + C \\
\int x^2 \sqrt{a^2 - x^2} \mathrm{d}x &= \cfrac{x}{8} (2x^2 - a^2) \sqrt{a^2 - x^2} + \cfrac{a^4}{8} \arcsin{\cfrac{x}{a}} + C \\
\int \cfrac{\sqrt{a^2 - x^2}}{x} \mathrm{d}x &= \sqrt{a^2 - x^2} + a \ln{\cfrac{a - \sqrt{a^2 - x^2}}{\lvert x \rvert}} + C \\
\int \cfrac{\sqrt{a^2 - x^2}}{x^2} \mathrm{d}x &= -\cfrac{\sqrt{a^2 - x^2}}{x} - \arcsin{\cfrac{x}{a}} + C
\end{align}
\]
(九)含有 \(\sqrt{\pm ax^2+bx+c}(a>0)\) 的积分
\[\begin{align}
\int \cfrac{\mathrm{d}x}{\sqrt{ax^2 + bx + c}} &= \cfrac{1}{\sqrt a} \ln{\lvert 2ax + b + 2\sqrt a \sqrt{ax^2 + bx + c} \rvert} \\
\int \sqrt{ax^2 + bx + c} \mathrm{d}x &= \cfrac{2ax + b}{4a} \sqrt{ax^2 + bx + c} -
\cfrac{4ac - b^2}{2 \sqrt{a^3}} \ln{\lvert 2ax + b + 2\sqrt a \sqrt{ax^2 + bx + c} \rvert}+ C \\
\int \cfrac{x}{\sqrt{ax^2 + bx + c}} \mathrm{d}x &= \cfrac{1}{a} \sqrt{ax^2 + bx + c} -\cfrac{b}{2 \sqrt{a^3}} \ln{\lvert 2ax + b + 2\sqrt a \sqrt{ax^2 + bx + c} \rvert}+ C \\
\int \cfrac{\mathrm{d}x}{\sqrt{c + bx - ax^2}} &= \cfrac{1}{\sqrt{a}} \arcsin{\cfrac{2ax - b}{b^2 + 4ac}} + C \\
\int \sqrt{c + bx - ax^2} \mathrm{d}x &= \cfrac{2ax - b}{4a} \sqrt{c + bx - ax^2} +
\cfrac{b^2 + 4ac}{8 \sqrt{a^3}} \arcsin{\cfrac{2ax - b}{\sqrt{b^2 + 4ac}}} + C \\
\int \cfrac{x}{\sqrt{c + bx - ax^2}} \mathrm{d}x &= -\cfrac{1}{a} \sqrt{c+bx-ax^2} + \cfrac{b}{2\sqrt{a^3}} \arcsin{\cfrac{2ax - b}{\sqrt{b^2 + 4ac}}} + C
\end{align}
\]
(十)含有 \(\sqrt{\pm \cfrac{x - a}{x - b}}\) 或 \(\sqrt{(x - a)(x - b)}\) 的积分
\[\begin{align}
\int \sqrt{\cfrac{x-a}{x-b}} \mathrm{d}x &= (x - b) \sqrt{\cfrac{x - a}{x - b}} + (b - a)\ln{(\sqrt{\lvert x - a \rvert} + \sqrt{\lvert x - b \rvert})} + C \\
\int \sqrt{\cfrac{x - a}{b - x}} \mathrm{d}x &= (x - b)\sqrt{\cfrac{x - a}{b - x}} + (b - a) \arcsin{\sqrt{\cfrac{x - a}{b - x}}} + C \\
\int \cfrac{\mathrm{d}x}{\sqrt{(x - a)(b - x)}} &= 2 \arcsin{\sqrt{\cfrac{x - a}{b - x}}} + C \\
\int \sqrt{(x - a)(b - x)} \mathrm{d}x &= \cfrac{2x - a - b}{4} \sqrt{(x - a)(b - x)} + \cfrac{(b - a)^2}{4} \arcsin{\sqrt{\cfrac{x - a}{b - a}}} + C
\end{align}
\]
(十一)含有三角函数的积分
\[\begin{align}
\int \sin x \mathrm{d}x &= -\cos x + C \\
\int \cos x \mathrm{d}x &= \sin x + C \\
\int \tan x \mathrm{d}x &= -\ln{\lvert \cos x \rvert} + C \\
\int \cot x \mathrm{d}x &= \ln{\sin x} + C \\
\int \sec x \mathrm{d}x &= \ln{\left \lvert \tan{\left( \cfrac{\pi}{4} + \cfrac{x}{2} \right)} \right \rvert} + C = \ln{\lvert \sec x + \tan x \rvert} + C \\
\int \csc x \mathrm{d}x &= \ln{\left \vert \tan{\cfrac{x}{2}} \right \vert} + C = \ln{\lvert \csc x - \cot x \rvert} + C \\
\int \sec^2 x \mathrm{d}x &= \tan x + C \\
\int \csc^2 x \mathrm{d}x &= -\cot x + C \\
\int \sec x \tan x \mathrm{d}x &= \sec x + C \\
\int \csc x \cot x \mathrm{d}x &= -\csc x + C \\
\int \sin^2 x \mathrm{d}x &= \cfrac{x}{2} - \cfrac{1}{4}\sin{2x} + C \\
\int \cos^2 x \mathrm{d}x &= \cfrac{x}{2} + \cfrac{1}{4}\sin{2x} + C \\
\int \sin^n x \mathrm{d}x &= -\cfrac{1}{n} \sin^{n - 1}x \cos x + \cfrac{n - 1}{n} \int \sin^{n - 2}x \mathrm{d}x \\
\int \cos^n x \mathrm{d}x &= \cfrac{1}{n} \cos^{n - 1}x \sin x + \cfrac{n - 1}{n} \int \cos^{n - 2}x \mathrm{d}x \\
\int \cfrac{\mathrm{d}x}{\sin^n x} &= -\cfrac{1}{n-1} \cdot \cfrac{\cos x}{\sin^{n - 1}x} + \cfrac{n - 2}{n - 1} \int \cfrac{\mathrm{d}x}{\sin^{n - 2}x} \\
\int \cfrac{\mathrm{d}x}{\cos^n x} &= \cfrac{1}{n-1} \cdot \cfrac{\sin x}{\cos^{n - 1}x} + \cfrac{n - 2}{n - 1} \int \cfrac{\mathrm{d}x}{\cos^{n - 2}x} \\
\int \cos^m x \sin^n \mathrm{d}x &=
\begin{cases}
\cfrac{1}{m + n} \cos^{m - 1}x \sin^{n + 1}x + \cfrac{m - 1}{m + n} \int \cos^{m - 2}x \sin^n x \mathrm{d}x \\
-\cfrac{1}{m + n} \cos^{m + 1}x \sin^{n - 1}x + \cfrac{n - 1}{m + n} \int \cos^{m }x \sin^{n - 2} x \mathrm{d}x
\end{cases} \\
\int \sin{ax} \cos{bx} \mathrm{d}x &= -\cfrac{1}{2(a + b)} \cos{(a + b)x} - \cfrac{1}{2(a - b)} \cos{(a - b)x} + C \\
\int \sin{ax} \sin{bx} \mathrm{d}x &= -\cfrac{1}{2(a + b)} \sin{(a + b)x} + \cfrac{1}{2(a - b)} \sin{(a - b)x} + C \\
\int \cos{ax} \cos{bx} \mathrm{d}x &= \cfrac{1}{2(a + b)} \sin{(a + b)x} + \cfrac{1}{2(a - b)} \sin{(a - b)x} + C \\
\int \cfrac{\mathrm{d}x}{a + b\sin x} &=
\begin{cases}
\cfrac{2}{\sqrt{a^2 - b^2}} \arctan{\cfrac{a \tan{\cfrac{x}{2}+b}}{\sqrt{a^2 - b^2}}} + C \quad &(a^2>b^2) \\
\cfrac{1}{\sqrt{b^2 - a^2}} \ln{\left \vert \cfrac{a \tan{\cfrac{x}{2}} + b - \sqrt{b^2 - a^2}}{a \tan{\cfrac{x}{2}} + b + \sqrt{b^2 - a^2}} \right \vert} + C \quad &(a^2<b^2)
\end{cases}\\
\int \cfrac{\mathrm{d}x}{a + b\cos x} &=
\begin{cases}
\cfrac{2}{a + b} \sqrt{\cfrac{a + b}{a - b}} \arctan{\left( \sqrt{\cfrac{a - b}{a + b}}\tan{\cfrac{x}{2}} \right)} + C \quad &(a^2 > b^2) \\
\cfrac{1}{a + b}\sqrt{\cfrac{a + b}{b - a}} \ln{\left \vert \cfrac{\tan{\cfrac{x}{2} + \sqrt{\cfrac{a + b}{b - a}}}}{\tan{\cfrac{x}{2} - \sqrt{\cfrac{a + b}{b - a}}}} \right \vert} + C \quad &(a^2<b^2)
\end{cases}\\
\int \cfrac{\mathrm{d}x}{a^2 \cos^2 x + b^2 \sin^2 x} &= \cfrac{1}{ab} \arctan{\left(\cfrac{b}{a} \tan{\cfrac{x}{2}}\right)} + C \\
\int \cfrac{\mathrm{d}x}{a^2 \cos^2 x - b^2 \sin^2 x} &= \cfrac{1}{2ab} \ln{\left \vert \cfrac{b\tan x + a}{b\tan x - a} \right \vert} + C \\
\int x \sin{ax} \mathrm{d}x &= \cfrac{1}{a^2} \sin{ax} - \cfrac{1}{a} x \cos{ax} + C \\
\int x^2 \sin{ax} \mathrm{d}x &= -\cfrac{1}{a} x^2 \cos{ax} + \cfrac{2}{a^2} x \sin{ax} + \cfrac{2}{a^3} \cos{ax} + C \\
\int x \cos{ax} \mathrm{d}x &= \cfrac{1}{a^2} \cos{ax} + \cfrac{1}{a} x \sin{ax} + C \\
\int x^2 \cos{ax} \mathrm{d}x &= \cfrac{1}{a} x^2 \sin{ax} + \cfrac{2}{a^2} x \cos{ax} - \cfrac{2}{a^3} \sin{ax} + C
\end{align}
\]
(十二)含有反三角函数的积分 其中\((a>0)\)
\[\begin{align}
\int \arcsin{\cfrac{x}{a}} \mathrm{d}x &= x \arcsin{\cfrac{x}{a}} + \sqrt{a^2 - x^2} + C \\
\int x\arcsin{\cfrac{x}{a}} \mathrm{d}x &= \left( \cfrac{x^2}{2} - \cfrac{a^2}{4} \right) \arcsin{\cfrac{x}{a}} + \cfrac{x}{4} \sqrt{a^2 - x^2} + C \\
\int x^2\arcsin{\cfrac{x}{a}} \mathrm{d}x &= \cfrac{x^3}{3} \arcsin{\cfrac{x}{a}} + \cfrac{1}{9} (x ^2 + 2a^2) \sqrt{a^2 - x^2} + C \\
\int \arccos{\cfrac{x}{a}} \mathrm{d}x &= x \arccos{\cfrac{x}{a}} - \sqrt{a^2 - x^2} + C \\
\int x\arccos{\cfrac{x}{a}} \mathrm{d}x &= \left( \cfrac{x^2}{2} - \cfrac{a^2}{4} \right) \arccos{\cfrac{x}{a}} - \cfrac{x}{4} \sqrt{a^2 - x^2} + C \\
\int x^2\arccos{\cfrac{x}{a}} \mathrm{d}x &= \cfrac{x^3}{3} \arccos{\cfrac{x}{a}} - \cfrac{1}{9} (x ^2 + 2a^2) \sqrt{a^2 - x^2} + C \\
\int \arctan{\cfrac{x}{a}} \mathrm{d}x &= x \arctan{\cfrac{x}{a}} - \cfrac{a}{2} \ln{a^2 + x^2} + C \\
\int x \arctan{\cfrac{x}{a}} \mathrm{d}x &= \cfrac{1}{2} (a^2 + x^2) \arctan{\cfrac{x}{a}} - \cfrac{a}{2} x + C \\
\int x^2 \arctan{\cfrac{x}{a}} \mathrm{d}x &= \cfrac{x^3}{3} \arctan{\cfrac{x}{a}} - \cfrac{a}{6} x^2 + \cfrac{a^3}{6} \ln{(a^2 + x^2)} + C
\end{align}
\]
(十三)含有指数函数的积分
\[\begin{align}
\int a^x \mathrm{d}x &= \cfrac{1}{\ln a} a^x + C \\
\int \mathrm{e}^{ax} \mathrm{d}x &= \cfrac{1}{q} \mathrm{e}^{ax} + C \\
\int x \mathrm{e}^{ax} \mathrm{d}x &= \cfrac{1}{a^2} (ax - 1) \mathrm{e}^{ax} + C \\
\int x^n \mathrm{e}^{ax} \mathrm{d}x &= \cfrac{1}{a} x^n \mathrm{e}^{ax} - \cfrac{n}{a} \int x^{n - 1} \mathrm{e}^{ax} \mathrm{d}x \\
\int x a^x \mathrm{d}x &= \cfrac{x}{\ln a} a^x - \cfrac{1}{\ln^2 a} a^x + C \\
\int x^n a^x \mathrm{d}x &= \cfrac{1}{\ln a} x^n a^x - \cfrac{n}{\ln a} \int x^{n - 1} a^x \mathrm{d}x\\
\int \mathrm{e}^{ax} \sin{bx} \mathrm{d}x &= \cfrac{1}{a^2 + b^2} \mathrm{e}^{ax}(a \sin{bx} - b \cos{bx}) + C \\
\int \mathrm{e}^{ax} \cos{bx} \mathrm{d}x &= \cfrac{1}{a^2 + b^2} \mathrm{e}^{ax}(b \sin{bx} + a \cos{bx}) + C \\
\int \mathrm{e}^{ax} \sin^n{bx} \mathrm{d}x &= \cfrac{1}{a^2 + b^2n^2} \mathrm{e}^{ax} \sin^{n-1}{bx} (a \sin{bx} - nb \cos{bx}) + \cfrac{n(n - 1) b^2}{a^2 + b^2 n^2} \int \mathrm{e}^{ax} \sin^{n - 2}{bx} \mathrm{d}x \\
\int \mathrm{e}^{ax} \cos^n{bx} \mathrm{d}x &= \cfrac{1}{a^2 + b^2n^2} \mathrm{e}^{ax} \cos^{n-1}{bx} (a \cos{bx} + nb \sin{bx}) + \cfrac{n(n - 1) b^2}{a^2 + b^2 n^2} \int \mathrm{e}^{ax} \cos^{n - 2}{bx} \mathrm{d}x
\end{align}
\]
(十四)含有对数函数的积分
\[\begin{align}
\int \ln{x} \mathrm{d}x &= x \ln{x} - x + C \\
\int \cfrac{\mathrm{d}x}{x \ln x} &= \ln{\lvert \ln x \rvert} + C \\
\int x^n \ln x \mathrm{d}x &= \cfrac{1}{n + 1} x^{n + 1} \left( \ln x - \cfrac{1}{n + 1} + C \right) \\
\int \ln^n x \mathrm{d}x &= x \ln^n x - n \int \ln^{n - 1} x \mathrm{d}x \\
\int x^m \ln^n x \mathrm{d}x &= \cfrac{1}{m + 1} x^{m + 1} \ln^n x - \cfrac{n}{m + 1} \int x^m \ln^{n - 1} x \mathrm{d}x
\end{align}
\]
(十五)含有双曲函数的
\[\begin{align}
\int \sinh x \mathrm{d}x &= \cosh x + C \\
\int \cosh x \mathrm{d}x &= \sinh x + C \\
\int \tanh x \mathrm{d}x &= \ln{\cosh x} + C \\
\int \sinh^2 x \mathrm{d}x &= -\cfrac{x}{2} + \cfrac{1}{4} \sinh{2x} + C \\
\int \cosh^2 x \mathrm{d}x &= \cfrac{x}{2} + \cfrac{1}{4} \sinh{2x} + C
\end{align}
\]
(十六)定积分
\[\begin{align}
\int_{-\pi}^{\pi} \cos{nx} \mathrm{d}x &= \int_{-\pi}^{\pi} \sin{nx} \mathrm{d}x = 0 \\
\int_{-\pi}^{\pi} \cos{mx} \sin{nx} \mathrm{d}x &= 0 \\
\int_{-\pi}^{\pi} \cos{mx} \cos{nx} \mathrm{d}x &=
\begin{cases}
0,\quad m \neq n, \\
\pi, \quad m = n
\end{cases}\\
\int_{-\pi}^{\pi} \sin{mx} \sin{nx} \mathrm{d}x &=
\begin{cases}
0,\quad m \neq n, \\
\pi, \quad m = n
\end{cases}\\
\int_0^{\pi} \sin{mx} \sin{nx} \mathrm{d}x &= \int_0^{\pi} \cos{mx} \cos{nx} \mathrm{d}x =
\begin{cases}
0, \quad m \neq n, \\
\cfrac{\pi}{2}, \quad m = n
\end{cases}\\
I_n = \int_0^{\cfrac{\pi}{2}} \sin^n x \mathrm{d}x &= \int_0^{\cfrac{\pi}{2}} \cos^n x \mathrm{d}x \\
I_n = \cfrac{n - 1}{n} I_{n - 2} &=
\begin{cases}
\cfrac{n - 1}{n} \cdot \cfrac{n - 3}{n - 2} \centerdot \cdots \centerdot \cfrac{4}{5} \cdot \cfrac{2}{3} \quad (n为大于1的正奇数),I_1 = 1, \\
\cfrac{n - 1}{n} \cdot \cfrac{n - 3}{n - 2} \centerdot \cdots \centerdot \cfrac{3}{4} \cdot \cfrac{1}{2} \cdot \cfrac{\pi}{2} \quad (n为正偶数),I_0 = \cfrac{\pi}{2} \\
\end{cases}
\end{align}
\]
2、换元积分法
把复合函数的微分法反过来用于求不定积分,利用中间变量的代换,得到复合函数的积分法,称为换元积分法 , 换元法。
第一类换元法
定理:设 \(f(u)\) 具有原函数,\(u=\varphi (x)\) 可导,则有换元公式
\[\int f [\varphi(x)] \varphi^{'} (x) \mathrm{d}x = \left[ \int f(u) \mathrm{d}u \right]_{u=\varphi (x)}
\]
由定理可知,虽然 \(\displaystyle \int f [\varphi(x)] \varphi^{'} (x) \mathrm{d}x\) 整体的记号,但从形式上看,被积表达式中的 \(\mathrm{d}x\) 也可以当做 \(x\) 的微分来对待,从而微分等式 \(\varphi^{'}(x)\mathrm{d}x = \mathrm{d}u\),可以方便地应用到被积表达式中来。
设要求 \(\displaystyle \int g(x) \mathrm{d}x\),如果函数 \(g(x)\) ,可以化为 \(g(x) = f[\varphi(x)] \varphi^{'}(x)\) 的形式,那么
\[\int g(x) \mathrm{d}x = \int f[\varphi (x)] \varphi^{'}(x) \mathrm{d}x = \left[ \int f(u)\mathrm{d}u \right]_{u = \varphi(x)}
\]
一般地,对于积分 \(\int f(ax + b) \mathrm{d}x (a \neq 0)\),总可做变换 \(u = ax + b\) ,把它化为
\[\int f(ax + b) \mathrm{d}x = \int \cfrac{1}{a} f(ax + b) \mathrm{d}(ax + b) = \cfrac{1}{a} \left[ \int f(u) \mathrm{d}u \right]_{u = ax + b}
\]
求 \(\displaystyle \int \frac{x^2}{(x + 2)^3} \mathrm{d}x\) .
解:令 \(u = x + 2\) ,则 \(x = u - 2,\mathrm{d}x = \mathrm{d}u\) .于是
\[\int \cfrac{x^2}{(x + 2)^2} \mathrm{d}x = \int \cfrac{(u - 2)^2}{u^3} \mathrm{d}u = \int (u^2 - 4u + 4)u^{-3} \mathrm{d}u \\
=\int(u^{-1} - 4u^{-2} + 4u^{-3}) \mathrm{d}u \\
=\ln \lvert u \rvert + 4u^{-1} - 2u^{-2} + C \\
=\ln{\lvert x + 2 \rvert} + \cfrac{4}{x + 2} - \cfrac{2}{(x + 2)^2} + C
\]
一般地,对于 \(\sin^{2k + 1}x \cos^n x\) 或 \(\sin^n x \cos^{2k + 1}x\) (其中 \(k \in \mathbf{N}\))型函数的积分总可依次做变换 \(u = \cos x\) 或 \(u = \sin x\) 。
求 \(\displaystyle \int \sin^2 x \cos^5 x \mathrm{d}x\)
解:
\[\begin{split}
\int \sin^2 x \cos^5 x \mathrm{d}x &= \int \sin^2 x \cos^4 x \cos x \mathrm{d}x \\
&= \int \sin^2 x (1 - \sin^2 x)^2 \mathrm{d} \sin x \\
&= \int (\sin^2 x - 2\sin^4 x + \sin^6 x) \mathrm{d} \sin x \\
&= \cfrac{1}{3} \sin^3 x - \cfrac{2}{5} \sin^5 x + \cfrac{1}{7} \sin^7 x + C
\end{split}
\]
一般地对于 \(\sin^{2k} x \cos^{2l} x (k,l \in \mathbf{N})\) 型函数,可利用三角恒等式:\(\sin^2 x = \cfrac{1}{2} (1 - \cos 2x),\cos^2 x = \cfrac{1}{2} (1 + \cos 2x)\) 化成 \(\cos 2x\) 多项式,然后求得积分。
求 \(\displaystyle \int \sin^2x \cos^4 x \, \mathrm{d}x\) .
解:
\[\begin{split}
\int \sin^2x \cos^4 x \, \mathrm{d}x &= \cfrac{1}{8} \int (1 - \cos{2x})(1 + \cos{2x}) \, \mathrm{d}x \\
&= \cfrac{1}{8} \int (1 + \cos{2x} - \cos^2{2x} - \cos^3{2x}) \, \mathrm{d}x \\
&= \cfrac{1}{8} \int (\cos{2x} - \cos^3{2x}) \, \mathrm{d}x + \cfrac{1}{8} \int (1 - \cos^2{2x}) \, \mathrm{d}x \\
&= \cfrac{1}{8} \int \sin^2{2x} \cdot \cfrac{1}{2} \mathrm{d}(\sin{2x}) + \cfrac{1}{8} \int \cfrac{1}{2} (1 - \cos{4x}) \, \mathrm{d}x \\
&= \cfrac{1}{48} \sin^3{2x} + \cfrac{x}{16} - \cfrac{1}{64} \sin{4x} + C
\end{split}
\]
一般地,对于 \(\tan^n x \sec^{2k} x\) 或 \(\tan^{2k - 1} x \sec^n x \, (n,k \in \mathbf{N_+})\) 型,可依次做变换 \(u = \tan x\) 或 \(u = \sec x\) 求得结果。
求 \(\displaystyle \int \tan^5 x \sec^3 x \, \mathrm{d}x\) .
解:
\[\begin{split}
\int \tan^5 x \sec^3 x \, \mathrm{d}x &= \int \tan^4 x \sec^2 x \sec x \tan x \, \mathrm{d}x \\
&= \int (\sec^2 x - 1)^2 \sec^2 x \, \mathrm{d}(\sec x) \\
&= \int (\sec^6 x - 2\sec^4 x \sec^2 x) \, \mathrm{d}(\sec x) \\
&= \cfrac{1}{7} \sec^7 x - \cfrac{2}{5} \sec^5 x + \cfrac{1}{3} \sec^3 x + C
\end{split}
\]
第二类换元法
定理:
设 \(x = \psi (t)\) 是单调可导函数,并且 \(\psi^{'}(t) \neq 0\) .又设 \(f[\psi(t)]\psi^{'}(t)\)具有原函数,则有:
\[\int f(x) \, \mathrm{d}x = \left[ \int f[\psi(t)]\psi^{'}(t) \, \mathrm{d}t \right]_{t = \psi^{-1}(x)}
\]
其中 \(\psi^{-1}(x)\)是 \(x = \psi (t)\) 的反函数.
证明:
设 \(f[\psi(t)]\psi^{'}(t)\) 的原函数为 \(\Phi (t)\),记 \(\Phi[\psi^{-1}(x)] = F(x)\) ,利用复合函数及反函数求导法则,得到:
\[F^{'} (x) = \cfrac{\mathrm{d} \Phi}{\mathrm{d}t} \cdot \cfrac{\mathrm{d}t}{\mathrm{d}x} = f[\psi(t)]\psi^{'}(t) \cdot \cfrac{1}{\psi{'}(t)} = f[\psi (t)] = f(x),
\]
即 \(F(x)\) 是 \(f(x)\) 的原函数.所以有:
\[\int f(x) \, \mathrm{d}x = F(x) + C = \Phi[\psi^{-1}(x)] + C = \left[ \int f[\psi(t)]\psi^{'}(t) \, \mathrm{d}t \right]_{t = \psi^{-1}(x)}
\]
三种类型的三角换元积分如下图所示:

分部积分法
利用两个函数乘积的求导法则可以推得另一求积分的基本方法——分部积分法 。
设函数 \(u = u(x)\) \(v = v(x)\) 具有连续导数,则这两个函数乘积的导数公式为
\[(uv)^{'} = u{'}v + uv^{'}
\]
移项得
\[uv^{'} = (uv)^{'} - u{'}v
\]
两边求不定积分
\[\int uv^{'} \mathrm{d}x = uv - \int u^{'}v \mathrm{d}x
\]
上式即为分部积分公式 。为方便起见,可以写成:
\[\int u \mathrm{d}v = uv - \int v \mathrm{d}u
\]
- 如果被积函数是幂函数和正(余)弦函数或幂函数和指数函数乘积,可以设幂函数为 \(u\) ,这样用一次分部积分法就可以使幂函数的幂次降低一次,这里假定幂指数是正整数。
求 \(\displaystyle \int x^2 \mathrm{e}^x \mathrm{d}x\) 。
解:
设 \(u = x^2,dv = \mathrm{e}^x \mathrm{d}x\) ,则
\[\int x^2 \mathrm{e}^x \mathrm{d}x = \int x^2 \mathrm{d}(\mathrm{e}^x) = x^2 \mathrm{e}^x - \int \mathrm{e}^x \mathrm{d}(x^2) = x^2 \mathrm{e}^x - 2 \int x \mathrm{e}^x \mathrm{d}x
\]
对 \(\displaystyle \int x \mathrm{e}^x \mathrm{d}x\) 再使用一次分部积分法:
\[\begin{split}
\int x^2 \mathrm{e}^x \mathrm{d}x &= x^2 \mathrm{e}^x - 2 \int x \mathrm{e}^x \mathrm{d}x = x^2 \mathrm{e}^x - 2\int x \mathrm{d}(\mathrm{e}^x) \\
&= x^2 \mathrm{e}^x - 2(x \mathrm{e}^x - \mathrm{e}^x) + C \\
&= \mathrm{e}^x (x^2 - 2x + 2) + C
\end{split}
\]
- 如果被积函数是幂函数和对数函数或幂函数和反三角函数乘积,可以设对数或反三角函数为 \(u\) ,这样用一次分部积分法就可以使幂函数的幂次降低一次,这里假定幂指数是正整数。
求 \(\displaystyle \int x \arctan{x} \mathrm{d}x\) .
解:
\[\begin{split}
\int x \arctan{x} \mathrm{d}x &= \cfrac{1}{2} \int \arctan{x} \mathrm{d}(x^2) \\
&= \cfrac{x^2}{2} \arctan x - \cfrac{1}{2} \int \cfrac{x^2}{1 + x^2} \mathrm{d}x \\
&= \cfrac{x^2}{2} \arctan x - \cfrac{1}{2} \int \cfrac{x^2 +1 - 1}{1 + x^2} \mathrm{d}x \\
&= \cfrac{x^2}{2} \arctan x - \cfrac{1}{2} \int \left(1 - \cfrac{1}{1 + x^2} \right) \mathrm{d}x \\
&= \cfrac{x^2}{2} \arctan x - \cfrac{1}{2} (x - \arctan x) + C \\
&= \cfrac{1}{2} (x^2 + 1) \arctan x - \cfrac{1}{2} x + C
\end{split}
\]
有理函数的积分
有理函数的积分
两个多项式的商 \(\cfrac{P(x)}{Q(x)}\) 称为有理函数,又称有理分式。假定分子多项式 \(P(x)\) 和分母多项式 \(Q(x)\) 之间没有公因式。当分子多项式 \(P(x)\) 的次数小于分母多项式 \(Q(x)\) 的次数时,称这个有理函数为真分式,否则称为假分式。
利用多项式的除法,总可以将一个假分式化成一个多项式与一个真分式之和的形式,如:
\[\cfrac{2x^4 + x^2 + 3}{x^2 + 1} = 2x^2 - 1 + \cfrac{4}{x^2 + 1}
\]
对于真分式 \(\cfrac{P(x)}{Q(x)}\) ,如果分母可分解为两个多项式的乘积
\[Q(x) = Q_1(x)Q_2(x)
\]
且 \(Q_1(x)\) 与 \(Q_2(x)\) 没有公因式,那么它拆分成两个真分式之和
\[\cfrac{P(x)}{Q(x)} = \cfrac{P_1(x)}{Q_1(x)} + \cfrac{P_2(x)}{Q_2(x)}
\]
如果 \(Q_1(x)\) 或 \(Q_2(x)\) 还能再分解成两个没有公因式的多项式的乘积,那么就可以再拆分成更简单的部分分式。最后,有理函数的分解式中只出现多项式、\(\cfrac{P_1(x)}{(x - a)^k}\)、\(\cfrac{P_2(x)}{(x^2 + px + q)^l}\)等三类函数(这里 \(p^2 - 4q < 0\),\(P_1(x)\) 为小于 \(k\) 次的多项式,\(P_2(x)\) 为小于 \(2l\) 次的多项式 )。
有理函数积分的完整方法:
第一步:
先看分子分母的最高项次数,必要时做多项式除法。 查看分子的次数是否小于分母次数。如果是则进入第二步;如果不是就要先做一个多项式除法,然后进入第二步。
第二步
对分母进行因式分解。 使用二次公式或猜想一个根,然后再做除法,以便因式分解被积函数的分母。
第三步
分部。 分别写出带有未知常数的分部。
分部的规则:
- 如果有线性式 \((x + a)\) ,则分部形式为 \(\cfrac{A}{x + a}\) 。
- 如果有线性式的平方 \((x + a)^2\) ,则分部形式为 \(\cfrac{A}{(x + a)^2} + \cfrac{B}{x + a}\) 。
- 如果有二次多项式 \((x^2 + ax + b)\) ,则分部形式为 \(\cfrac{Ax + B}{x^2 + ax + b}\) 。
- 如果有线性式的三次方 \((x + a)^3\) ,则分部形式为 \(\cfrac{A}{(x + a)^3} + \cfrac{B}{(x + a)^2} + \cfrac{C}{x + a}\) 。
- 如果有线性式的四次方 \((x + a)^4\) ,则分部形式为 \(\cfrac{A}{(x + a)^4} + \cfrac{B}{(x + a)^3} + \cfrac{C}{(x + a)^2} + \cfrac{D}{x + a}\) 。
注:分部仅仅由分母决定。
第四步
计算常数值 。把方程两边同时乘以通过任一方法计算常数的值:(a) 换掉 \(x\)的值;(b) 系数相等法;或者结合使用(a) 和 (b) 两种方法。
第五步
求解分母为线性项次幂的积分 。
第六步
对分母是二次函数的被积函数求积分 。
一个综合例题
求 \(\displaystyle \int \cfrac{x^5 - 7x^4 + 19x^3 - 10x^2 - 19x + 18}{x^4 - 5x^3 + 9x^2} \mathrm{d}x\) 的积分
解:
第一步:先看分子分母的最高项次数,必要时做多项式除法。 积分表达式中,分子最高次数5,分母最高次数为4,所以需要做多项式除法:
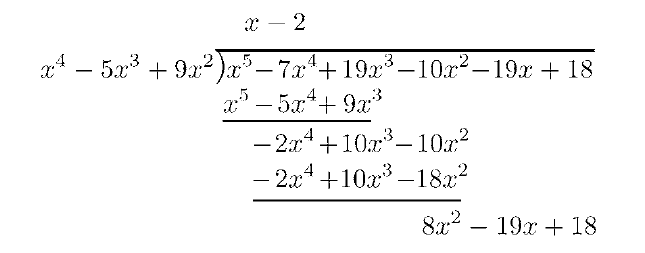
所以得到:
\[\int \cfrac{x^5 - 7x^4 + 19x^3 - 10x^2 - 19x + 18}{x^4 - 5x^3 + 9x^2} \mathrm{d}x = \int \left( x - 2 + \cfrac{8x^2 - 19x + 18}{x^4 - 5x^3 + 9x^2} \right) \mathrm{d}x
\]
等式右侧前两项的积分很容易求得,其结果为 \(\cfrac{1}{2}x^2 - 2x\) ,所以只需要求出 \(\displaystyle \int \cfrac{8x^2 - 19x + 18}{x^4 - 5x^3 + 9x^2} \mathrm{d}x\) 即可。
第二步:对分母进行因式分解。
\[x^4 - 5x^3 + 9x^2 = x^2(x^2 - 5x + 9)
\]
二次项 \(x^2 - 5x + 9\) 的判别式 \(\Delta = -11 < 0\) ,所以这个二项式不能因式分解。
第三步:分部 。\(x^2\) 产生分部 \(\cfrac{A}{x^2} + \cfrac{B}{x}\) ,\(x^2 - 5x + 9\) 产生分部 \(\cfrac{Cx + D}{x^2 - 5x + 9}\),所以有:
\[\cfrac{8x^2 - 19x + 18}{x^2(x^2 - 5x + 9)} = \cfrac{A}{x^2} + \cfrac{B}{x} + \cfrac{Cx + D}{x^2 - 5x + 9}
\]
第四步:计算常数值 。把上式两边同时乘以分母 \(x^2(x^2 - 5x + 9)\) ,
\[8 x^{2}-19 x+18=A\left(x^{2}-5 x+9\right)+B x\left(x^{2}-5 x+9\right)+(C x+D) x^{2}
\]
令 \(x = 0\) 可得 \(A = 2\) 。
\[\begin{aligned}
8 x^{2}-19 x+18 &=A x^{2}-5 A x+9 A+B x^{3}-5 B x^{2}+9 B x+C x^{3}+D x^{2} \\
&=(B+C) x^{3}+(A-5 B+D) x^{2}+(-5 A+9 B) x+9 A
\end{aligned}
\]
得到方程组:
\[\begin{array}{lr}
x^{3} \text { 的系数 }: 0=B+C \\
x^{2} \text { 的系数 }: 8=A-5 B+D \\
x^{1} \text { 的系数 }:-19=-5 A+9 B .
\end{array}
\]
解得:\(B = -1,C = 1,D = 1\),得到:
\[\frac{8 x^{2}-19 x+18}{x^{2}\left(x^{2}-5 x+9\right)}=\frac{2}{x^{2}}+\frac{-1}{x}+\frac{x+1}{x^{2}-5 x+9} .
\]
所以有:
\[\int \frac{8 x^{2}-19 x+18}{x^{2}\left(x^{2}-5 x+9\right)} \mathrm{d} x=2 \int \frac{1}{x^{2}} \mathrm{~d} x-\int \frac{1}{x} \mathrm{~d} x+\int \frac{x+1}{x^{2}-5 x+9} \mathrm{d} x
\]
第五步:求解分母为线性项次幂的积分。
\[2 \int \frac{1}{x^{2}} \mathrm{~d} x-\int \frac{1}{x} \mathrm{d} x=-\frac{2}{x}-\ln |x|+C
\]
第六步:对分母是二次函数的被积函数求积分 。计算 \(\displaystyle \int \frac{x+1}{x^{2}-5 x+9} \mathrm{~d} x\)
配方可得
\[x^{2}-5 x+9=\left(x^{2}-5 x+\frac{25}{4}\right)+9-\frac{25}{4}=\left(x-\frac{5}{2}\right)^{2}+\frac{11}{4}
\]
\[\int \frac{x+1}{x^{2}-5 x+9} \mathrm{d} x=\int \frac{x+1}{\left(x-\frac{5}{2}\right)^{2}+\frac{11}{4}} \mathrm{d} x
\]
令 \(t = x - \cfrac{5}{2}\) 做换元,这个积分变为:
\[\int \cfrac{t+\frac{5}{2}+1}{t^{2}+\frac{11}{4}} \mathrm{~d} t=\int \frac{t+\frac{7}{2}}{t^{2}+\frac{11}{4}} \mathrm{~d} t = \int \frac{t}{t^{2}+\frac{11}{4}} \mathrm{~d} t + \frac{7}{2} \int \frac{1}{t^{2}+\frac{11}{4}} \mathrm{~d} t
\]
其中
\[\int \frac{t}{t^{2}+\frac{11}{4}} \mathrm{~d} t=\frac{1}{2} \int \frac{2 t}{t^{2}+\frac{11}{4}} \mathrm{~d} t=\frac{1}{2} \ln \left|t^{2}+\frac{11}{4}\right|+C=\frac{1}{2} \ln \left[\left(x-\frac{5}{2}\right)^{2}+\frac{11}{4}\right]+C
\]
\[\frac{7}{2} \int \frac{1}{t^{2}+\frac{11}{4}} \mathrm{~d} t=\frac{7}{2} \times \frac{2}{\sqrt{11}} \arctan \left(\frac{t}{\sqrt{11} / 2}\right)+C=\frac{7}{\sqrt{11}} \arctan \left(\frac{2 t}{\sqrt{11}}\right)+C = \frac{7}{\sqrt{11}} \arctan \left(\frac{2 x-5}{\sqrt{11}}\right)+C
\]
第六步的最终答案为
\[\int \frac{x+1}{x^{2}-5 x+9} \mathrm{~d} x=\frac{1}{2} \ln \left(x^{2}-5 x+9\right)+\frac{7}{\sqrt{11}} \arctan \left(\frac{2 x-5}{\sqrt{11}}\right)+C
\]
结合六个步骤得到最终答案:
\[\begin{aligned}
&\int \frac{x^{5}-7 x^{4}+19 x^{3}-10 x^{2}-19 x+18}{x^{4}-5 x^{3}+9 x^{2}} \mathrm{~d} x \\
=& \int\left(x-2+\frac{2}{x^{2}}-\frac{1}{x}+\frac{x+1}{x^{2}-5 x+9}\right) \mathrm{d} x \\
=& \frac{x^{2}}{2}-2 x-\frac{2}{x}-\ln |x|+\frac{1}{2} \ln \left(x^{2}-5 x+9\right)+\frac{7}{\sqrt{11}} \arctan \left(\frac{2 x-5}{\sqrt{11}}\right)+C
\end{aligned}\]