莫队详解
莫队详解
一、普通莫队
莫队是由2010年信息学国家集训队队员莫涛发明的一种算法,可以将静态离线区间查询的时间复杂度将至 \(O(m \sqrt{n} )\)
下面便是一道莫队例题 Luogu 1972 [SDOI2009] HH的项链 虽然这道题莫队过不了,但是确实是很好的一道莫队题。
题意: 给你一个 \(n\) 个数的序列,有 \(m\) 次询问,每次询问在 \(l r\) 之间有多少个不同的数。
首先考虑暴力做法,对于每一个询问,暴力扫一遍,求答案,最坏情况时间复杂度 \(O(nm)\) (20%)
这时候,我们考虑优化,因为没有强制在线,我们可以先将所有询问按照 \(l\) 排序,再做统一处理,如下图(运气极好的情况下)

这时候,时间复杂度是 \(O(n)\) 的,但是,如果遇到特殊情况,可以把时间复杂度卡成约 \(O(nm)\) (如下图)
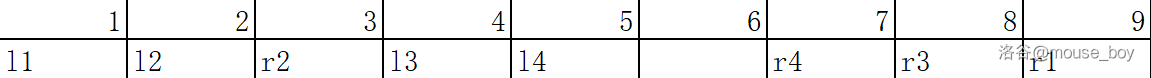
所以,这种优化及其不稳定,这时候,莫队改变了一下排序方式,使得复杂度优化成了 \(O(m \sqrt{n})\)
莫队将整个数组分成 \(\sqrt{n}\) 块,对于每个询问,将其看成平面直角坐标系上的点 \((l,r)\) 然后先对于 \(l\) 的区块排序,若区块相同再按 \(r\) 排序,这样,对于每个询问,最坏情况要扫 \(\sqrt(n)\) 次,总时间复杂度 \(O(m \sqrt{n} )\) (40%)
代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int kMaxN = 1e6 + 5;
ll n, m, k, cnt, l = 1, r, a[kMaxN], vis[kMaxN], pos[kMaxN], ans[kMaxN];
// vis 统计出现个数,ans 统计答案
struct node {
ll l, r, id;
} q[kMaxN];
bool cmp(node x, node y) {
if (pos[x.l] != pos[y.l]) {
return pos[x.l] < pos[y.l];// 优先按照 l 的区块排序
}
return (!(pos[x.l] & 1)) ^ (x.r < y.r);// 奇偶优化(下文会讲)
}
void del(int x) {
cnt -= !--vis[a[x]];
/*
等同于
vis[a[x]]--;
if(vis[a[x]] == 0){
cnt--;
}
*/
}
void add(int x) {
cnt += !vis[a[x]]++;
/*
等同于
if(vis[a[x]] == 0){
cnt++;
}
vis[a[x]]++;
*/
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n, k = sqrt(n);
for (int i = 1; i <= n; i++) {
cin >> a[i], pos[i] = (i - 1) / k + 1;
}
cin >> m;
for (int i = 1; i <= m; i++) {
cin >> q[i].l >> q[i].r, q[i].id = i;
}
sort(q + 1, q + 1 + m, cmp);
for (int i = 1; i <= m; i++) {
for (; l < q[i].l; del(l++)) {
}// 移动 l
for (; q[i].r < r; del(r--)) {
}// 移动 r
for (; q[i].l < l; add(--l)) {
}// 移动 l
for (; r < q[i].r; add(++r)) {
}// 移动 r
ans[q[i].id] = cnt;
}
for (int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
return 0;
}
二、奇偶优化
假设我们每个区块都按照 \(r\) 的升序排序,不妨各位想象一下,每次走完一个区块都会从最高点到下一个区块的最低点,儿在下一个区块又要走到最高点,会浪费时间,所以我们对于每个奇数块用 \(r\) 升序排序,对于每个偶数块用 \(r\) 降序排序,就可以避免这个问题
代码:
return (!(pos[x.l] & 1)) ^ (x.r < y.r);
/*
就等同于
if(pos[x.l] % 2 == 0){
return x.r > y.r;
}else{
return x.r < y.r;
}
*/
三、带修莫队
因为莫队算法是离线的,所以不支持大幅度修改,但是可以尝试进行简单的单点修改。
例题:Luogu P1903 [国家集训队] 数颜色 / 维护队列
题意:给你一个 \(n\) 个数的序列,有 \(m\) 次询问,每次询问在 \(l r\) 之间有多少个不同的数,或者将 \(x\) 修改成 \(y\)。
我们考虑再多加一个维度 \(z\) 轴,表示修改次数,所以对于每个询问将其变成立面直角坐标系上的点 \((x,y,z)\) ,在在排序方式上进行了修改,对于每两个点之间,优先按照 \(x\) 的区块排序若相同则按照 \(y\) 的区间排序,若还是相同,则对于 \(t\) 排序,这样就可以把时间复杂度变成(B是块长):\((Bm \times 2 + \frac{mn^2}{B^2} )\) 可求出,当 \(B\) 取 \(n^{\frac{2}{3}}\) 时,有较好的时间复杂度 \(O(mn^{\frac{2}{3}})\)
代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int kMaxN = 1e6 + 5;
ll n, m, k, cnt, l = 1, r, x, y, z, sum, sum2, a[kMaxN], vis[kMaxN], pos[kMaxN], ans[kMaxN];
char c;
struct node {
ll l, r, id, t;
} q[kMaxN], t[kMaxN];
bool cmp(node x, node y) {
if (pos[x.l] != pos[y.l]) {
return pos[x.l] < pos[y.l];
}
if (pos[x.r] != pos[y.r]) {
return pos[x.r] < pos[y.r];
}
return x.t < y.t;
}
void del(int x) {
cnt -= !--vis[x];
}
void add(int x) {
cnt += !vis[x]++;
}
void update(ll x, ll y) {//x 是排完序后的下标,y是当前修改次数
if (q[x].l <= t[y].l && t[y].l <= q[x].r) {
del(a[t[y].l]);
add(t[y].r);
}
swap(a[t[y].l], t[y].r);// 因为修改完后下一次操作必然相反,所以直接swap
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m, k = pow(n, 0.666);
for (int i = 1; i <= n; i++) {
cin >> a[i], pos[i] = (i - 1) / k + 1;
}
for (int i = 1; i <= m; i++) {
cin >> c >> x >> y;
if (c == 'Q') {
++sum, q[sum] = {x, y, sum, sum2};//这里表示:x坐标,y坐标,原数组下标,和z坐标
} else {
t[++sum2] = {x, y};
}
}
sort(q + 1, q + 1 + sum, cmp);
for (int i = 1; i <= sum; i++) {
for (; l < q[i].l; del(a[l++])) {
}
for (; q[i].r < r; del(a[r--])) {
}
for (; q[i].l < l; add(a[--l])) {
}
for (; r < q[i].r; add(a[++r])) {
}
for (; q[i].t < z; update(i, z--)) {
}
for (; z < q[i].t; update(i, ++z)) {
}
ans[q[i].id] = cnt;
}
for (int i = 1; i <= sum; i++) {
cout << ans[i] << "\n";
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号