CF1051D题解

觉得巨佬们考虑的太复杂了，其实可以用三维递归 （一维表示第几列，二维记录有多少个连通块，三维两个格子同色或异色），对于第 i 格，连通块的数量取决于第 i-1 个格子，如下图。

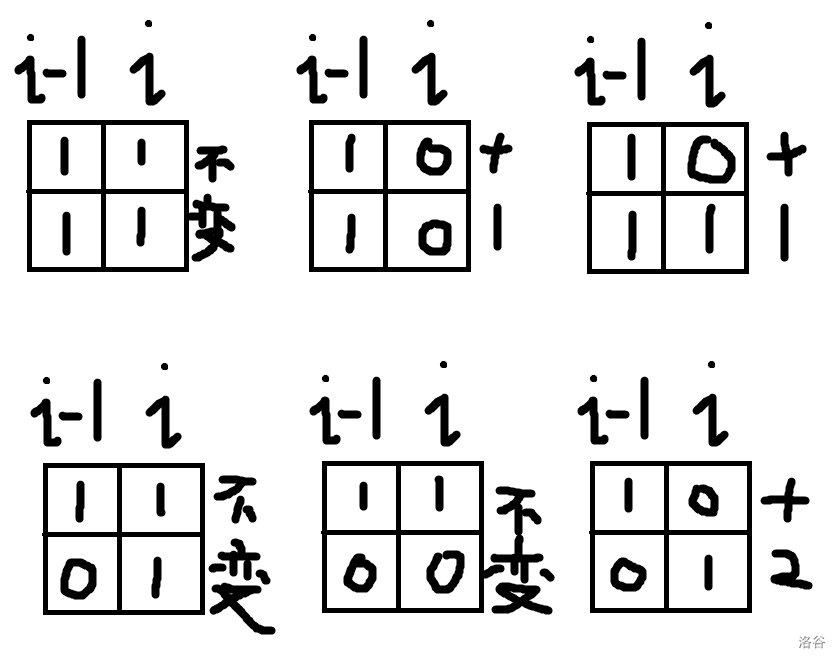
然后可得递归式:

f[i][j][0] = (f[i - 1][j][1] \times 2 + f[i - 1][j][0] + f[i - 1][j - 1][0]);

f[i][j][1] = (f[i - 1][j - 1][0] \times 2 + f[i - 1][j][1] + f[i - 1][j - 2][1]);

最后附上代码

#include <bits/stdc++.h>
using namespace std;
const int Maxn = 1005, mod = 998244353;
int f[Maxn][Maxn * 2][2], n, k;//注意二维开两倍
int main() {
  cin >> n >> k;
  f[1][2][0] = f[1][3][1] = 2;//初始化
  for (int i = 2; i <= n; i++) {
    for (int j = 2; j <= k + 1; j++) {//注意这里要加1
      f[i][j][0] = (f[i - 1][j][1] * 2LL + f[i - 1][j][0] + f[i - 1][j - 1][0]) % mod;
      f[i][j][1] = (f[i - 1][j - 1][0] * 2LL + f[i - 1][j][1] + f[i - 1][j - 2][1]) % mod;
    }
  }
  cout << (f[n][k + 1][0] + f[n][k + 1][1]) % mod;
  return 0;//华丽的结束
}