hiho# 1398 最大权闭合子图 网络流

题目传送门

题意：给出n个活动，m个人，请人需要花费$a[i]$的钱，举办一次活动可以赚$b[i]$的钱，但是需要固定的几个人在场，一个人只需要请一次后就必定在场，问最大收益。

思路：

　　下列结论来自hihocoder的例题

　　下面不加证明的给出几个概念和结论。

　　1）闭合子图：给定一个有向图，从中选择一些点组成一个点集V。对于V中任意一个点，其后续节点都仍然在V中。比如：

　　

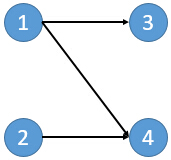
      在这个图中有8个闭合子图：∅,{3},{4},{2,4},{3,4},{1,3,4},{2,3,4},{1,2,3,4}

　　2) 最大权闭合子图：如上图的二分图，A部权值为正，B部权值为负，要求闭合子图权值最大，即为最大权闭合子图。

　　3）最大权闭合子图求法：首先建立源点s和汇点t，将源点s与所有权值为正的点相连，容量为权值；将所有权值为负的点与汇点t相连，容量为权值的绝对值；权值为0的点不做处理；同时将原来的边容量设置为无穷大。$ans=权值为正的点的和-最小割$

此题显然就是求一个最大权闭合子图。

#include<bits/stdc++.h>
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;

typedef long long ll;

const ll INFLL = 0x3f3f3f3f3f3f3f3f;
const int INF = 0x3f3f3f3f;
const int maxn = 510;

struct Edge {
    int to, flow, nxt;
    Edge(){}
    Edge(int to, int nxt, int flow):to(to),nxt(nxt), flow(flow){}
}edge[maxn * maxn * 2];

int head[maxn*2], dep[maxn*2];
int S, T;
int N, n, m, tot;
void init(int n)
{
    N=n;
    for (int i = 0; i <= N; ++i) head[i] = -1;
    tot = 0;
}

void addv(int u, int v, int w, int rw = 0)
{
    edge[tot] = Edge(v, head[u], w); head[u] = tot++;
    edge[tot] = Edge(u, head[v], rw); head[v] = tot++;
}

bool BFS()
{
    for (int i = 0; i <= N; ++i) dep[i] = -1;
    queue<int>q;
    q.push(S);
    dep[S] = 1;
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = edge[i].nxt)
        {
            
            if (edge[i].flow && dep[edge[i].to] == -1)
            {
                dep[edge[i].to] = dep[u] + 1;
                q.push(edge[i].to);
            }
        }
    }
    return dep[T] < 0 ? 0 : 1;
}

int DFS(int u, int f)
{
    if (u == T || f == 0) return f;
    int w, used = 0;
    for (int i = head[u]; ~i; i = edge[i].nxt)
    {
        if (edge[i].flow && dep[edge[i].to] == dep[u] + 1)
        {
            w = DFS(edge[i].to, min(f - used, edge[i].flow));
            edge[i].flow -= w;
            edge[i ^ 1].flow += w;
            used += w;
            if (used == f) return f;
        }
    }
    if (!used) dep[u] = -1;
    return used;
}

int Dicnic()
{
    int ans = 0;
    while (BFS())
    {
        ans += DFS(S, INF);
    }
    return ans;
}

int main(){
    cin>>n>>m;
    T=n+m+1;
    init(T);
    S=0;
    for(int i=1;i<=m;i++){
        int w;
        scanf("%d",&w);
        addv(i+n,T,w);
    }
    int res=0;
    for(int i=1;i<=n;i++){
        int w,k;
        scanf("%d%d",&w,&k);
        addv(S,i,w);
        res+=w;
        while(k--){
            scanf("%d",&w);
            addv(i,n+w,INF);
        }
    }
    int ans=res-Dicnic();
    printf("%d\n",ans);
}