十进制与二进制

十进制与二进制之间的转换：

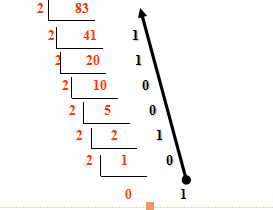
   （1）十进制转二进制的转换原理：除以2，反向取余数，直到商为0终止。

            9(十进制)→1001(二进制）

 

#include<iostream>
using namespace std;

int two_num[10086];
int ten_num;

int main(){
    cin>>ten_num;
    
    int t=ten_num,temp=0;
    while(t){
        two_num[ ++temp ] = t%2;
        t/=2;
    }
    
    for( int i=temp ; i>=1 ; --i ){
        cout<<two_num[i];
    }q
    return 0;
} 

 

   （2）二进制转十进制的转换原理： 就是用进制的定义：二进制的每一个乘以2的n次方，n从0开始，每次递增1。然后得出来的每个数相加。

    　　1110(二进制)→ 14(十进制)     8+4+2=14

 推荐记住2的指数9以内的数：1、2、4、8、16、32、64、128、256、1024

 

#include<iostream>
#include<cstring>
using namespace std;

char two_num[10086];
int ten_num;

int main(){
    
    gets(two_num);
    int n=strlen(two_num);
    
    for( int i=n-1 ; i>=0 ; --i ){
        
        if( two_num[n-1-i]=='1' ){
            ten_num = ten_num*2+1;
        }
        else{
            ten_num*=2;
        }
        
        //    cout<<"two_num[n-1-i]："<<two_num[n-1-i]<<"   ";        
        //    cout<<"ten_num:"<<ten_num<<endl;
    }
    cout<<ten_num;
    
    return 0;
}

如果你是搞网络的，我觉得你一定要记住以下几种二进制数的转换值。你是一个网络工程 师，当看到一串二进制数时，你不要告诉我你会拿出笔纸或掰手指算半天才知道它转化成十进制的数值。要想快，那就记下下面几种常见的二进制--十进制转换：

 

以8位 来演示:

 

1.第一种:

 

   00000001      1

   00000010      2

   00000100      4

   00001000      8

   00010000      16

   00100000      32

   01000000      64

   10000000      128

 

 

2.第二种：

 

  00000001      1

  00000011      3

  00000111      7

  00001111      15

  00011111      31

  00111111      63

  01111111      127

 

 

3.第三种：

 

  10000000     128

  11000000     192

  11100000     224

  11110000     240

  11111000     248

  11111100     252

  11111110     254

 

 

举个例子：  11101011     

                         可分为：

                         11100000（上面第三种类型）   224

                         00001000（上面第一种类型）   8

                         00000011（上面第二种类型）   3

我们通过记住上面三种类型的转换，再用加法立即得到结果：235

 

文章内容摘抄于：

十进制与二进制之间的转换 - DragonGirI的博客 - CSDN博客

【数制转换】-十进制数转换成二进制数 - zhaizhai的博客 - CSDN博客

二进制转十进制快速方法 - 24K程序猿 - CSDN博客