数据结构(计算机存储、组织数据方式)
数据结构含义
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
内容解释:
数据:数据(data)是事实或观察的结果,是对客观事物的逻辑归纳,是用于表示客观事物的未经加工的的原始素材。

数据的实质:事实或观察的结果 数据的意义:信息的表现形式和载体 数据是指对客观事件进行记录并可以鉴别的符号,是对客观事物的性质、状态以及相互关系等进行记载的物理符号或这些物理符号的组合。它是可识别的、抽象的符号。 它不仅指狭义上的数字,还可以是具有一定意义的文字、字母、数字符号的组合、图形、图像、视频、音频等,也是客观事物的属性、数量、位置及其相互关系的抽象表示。例如,“0、1、2...`”、“阴、雨、下降、气温”“学生的档案记录、货物的运输情况”等都是数据。数据经过加工后就成为信息。 在计算机科学中,数据是指所有能输入到计算机并被计算机程序处理的符号的介质的总称,是用于输入电子计算机进行处理,具有一定意义的数字、字母、符号和模拟量等的通称。现在计算机存储和处理的对象十分广泛,表示这些对象的数据也随之变得越来越复杂。 信息与数据既有联系,又有区别。 数据是信息的表现形式和载体,可以是符号、文字、数字、语音、图像、视频等。而信息是数据的内涵,信息是加载于数据之上,对数据作具有含义的解释。 数据和信息是不可分离的,信息依赖数据来表达,数据则生动具体表达出信息。 数据是符号,是物理性的,信息是对数据进行加工处理之后所得到的并对决策产生影响的数据,是逻辑性和观念性的。 数据是信息的表现形式,信息是数据有意义的表示。数据是信息的表达、载体,信息是数据的内涵,是形与质的关系。 数据本身没有意义,数据只有对实体行为产生影响时才成为信息。
数据元素:数据元素(data element)是计算机科学术语。它是数据的基本单位,数据元素也叫做结点或记录。在计算机程序中通常作为一个整体进行考虑和处理。有时,一个数据元素可由若干个数据项组成,例如,一本书的书目信息为一个数据元素,而书目信息的每一项(如书名、作者名等)为一个数据项。数据项是数据的不可分割的最小单位。
数据结构的研究对象
一、数据的逻辑结构:
指反映数据元素之间的逻辑关系的数据结构,其中的逻辑关系是指数据元素之间的前后件关系,而与他们在计算机中的存储位置无关。

逻辑关系(logic relationship)即“依赖关系”。
在项目管理中,指表示两个活动(前导活动和后续活动)中一个活动的变更将会影响到另一个活动的关系。
通常活动之间的依赖关系包括强制依赖关系(所做工作中固有的依赖关系)、可自由处理的依赖关系(由项目队伍确定的依赖关系)和外部依赖关系(项目活动与非项目活动之间的依赖关系)三种形式
三种逻辑关系解释:
硬逻辑、强制性依赖关系(Mandatory Dependencies)
是指所做工作中固有的依赖关系,也称为逻辑硬逻辑关系(Hard Logic)
软逻辑、任意的依赖关系(Discretionary Dependencies)
是指由项目团队确定的那些依赖关系,也称为软逻辑关系(Soft Logic)
外部逻辑、外部依赖关系(External Dependencies)
是指受项目外部因素制约的那些依赖关系
用鸡蛋炒韭菜解释三种逻辑关系:
韭菜要先切后炒,叫硬逻辑关系;
韭菜鸡蛋单炒,一般人最佳实践先炒鸡蛋,这叫软逻辑关系;
要做这道菜却没鸡蛋,等鸡下蛋后,才能做,这叫外部逻辑关系。
硬逻辑:必须先盖下层,才能盖上层
外部逻辑:依赖于其他因素,如只有天气合适,才适合滑雪
软逻辑:可以先高尔夫,再游泳,也可反之进行

1.集合 数据结构中的元素之间除了“同属一个集合” 的相互关系外,别无其他关系; 2.线性结构 数据结构中的元素存在一对一的相互关系; 3.树形结构 数据结构中的元素存在一对多的相互关系; 4.图形结构 数据结构中的元素存在多对多的相互关系。
二、数据的物理结构:
指数据的逻辑结构在计算机存储空间的存放形式。数据的物理结构是数据结构在计算机中的表示(又称映像),它包括数据元素的机内表示和关系的机内表示。由于具体实现的方法有顺序、链接、索引、散列等多种,所以,一种数据结构可表示成一种或多种存储结构。

数据元素的机内表示(映像方法): 用二进制位(bit)的位串表示数据元素。通常称这种位串为节点(node)。当数据元素有若干个数据项组成时,位串中与个数据项对应的子位串称为数据域(data field)。因此,节点是数据元素的机内表示(或机内映像)。
关系的机内表示(映像方法):数据元素之间的关系的机内表示可以分为顺序映像和非顺序映像,常用两种存储结构:顺序存储结构和链式存储结构。顺序映像借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系。非顺序映像借助指示元素存储位置的指针(pointer)来表示数据元素之间的逻辑关系。
如果上文“数据结构在计算机中的表示”看不懂,应该可以这样理解(我也看不懂):数据元素的机内表示就是拿二进制在电脑里存数据,关系的机内表示就是像用数组(顺序存储结构、顺序映像)或链表(链式存储结构、非顺序映像)存数据的数据处理方式。
常用结构
每一种数据结构都有着独特的数据存储方式,下面为大家介绍它们的结构和优缺点。
1.数组

1 #include<iostream> 2 using namespace std; 3 4 int array[100]; 5 6 int main(){ 7 8 array[0]=1; 9 10 return 0; 11 }
优点:
1、按照索引查询元素速度快
2、按照索引遍历数组方便
缺点:
1、数组的大小固定后就无法扩容了
2、数组只能存储一种类型的数据
3、添加,删除的操作慢,因为要移动其他的元素。
适用场景:
频繁查询,对存储空间要求不大,很少增加和删除的情况。
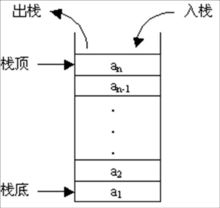
2.栈
栈的结构就像一个集装箱,越先放进去的东西越晚才能拿出来,所以,栈常应用于实现递归功能方面的场景,例如斐波那契数列。
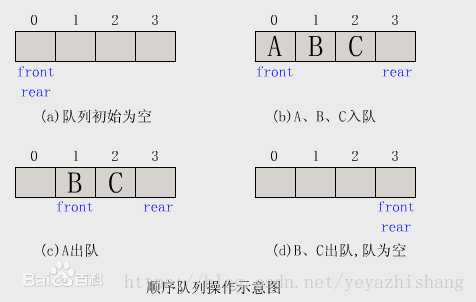
3.队列
4.链表
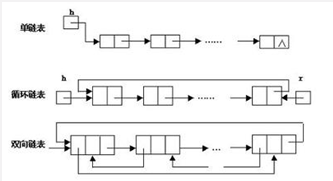
链表的优点:
链表是很常用的一种数据结构,不需要初始化容量,可以任意加减元素;
添加或者删除元素时只需要改变前后两个元素结点的指针域指向地址即可,所以添加,删除很快;
缺点:
因为含有大量的指针域,占用空间较大;
查找元素需要遍历链表来查找,非常耗时。
适用场景:
数据量较小,需要频繁增加,删除操作的场景
5.树
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点有零个或多个子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
在日常的应用中,我们讨论和用的更多的是树的其中一种结构,就是二叉树。 
二叉树是树的特殊一种,具有如下特点:
- 每个结点最多有两颗子树,结点的度最大为2。
- 左子树和右子树是有顺序的,次序不能颠倒。
- 即使某结点只有一个子树,也要区分左右子树。
二叉树是一种比较有用的折中方案,它添加,删除元素都很快,并且在查找方面也有很多的算法优化,所以,二叉树既有链表的好处,也有数组的好处,是两者的优化方案,在处理大批量的动态数据方面非常有用。
扩展:
二叉树有很多扩展的数据结构,包括平衡二叉树、红黑树、B+树等,这些数据结构二叉树的基础上衍生了很多的功能,在实际应用中广泛用到,例如mysql的数据库索引结构用的就是B+树,还有HashMap的底层源码中用到了红黑树。这些二叉树的功能强大,但算法上比较复杂,想学习的话还是需要花时间去深入的。
6.图
按照顶点指向的方向可分为无向图和有向图:
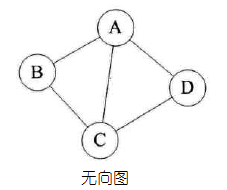
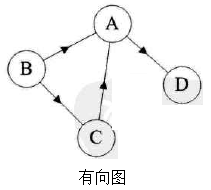
图是一种比较复杂的数据结构,在存储数据上有着比较复杂和高效的算法,分别有邻接矩阵 、邻接表、十字链表、邻接多重表、边集数组等存储结构,这里不做展开,读者有兴趣可以自己学习深入。
7.堆
堆是一种比较特殊的数据结构,可以被看做一棵树的数组对象,具有以下的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4…n/2),满足前者的表达式的成为小顶堆,满足后者表达式的为大顶堆,这两者的结构图可以用完全二叉树排列出来,示例图如下: 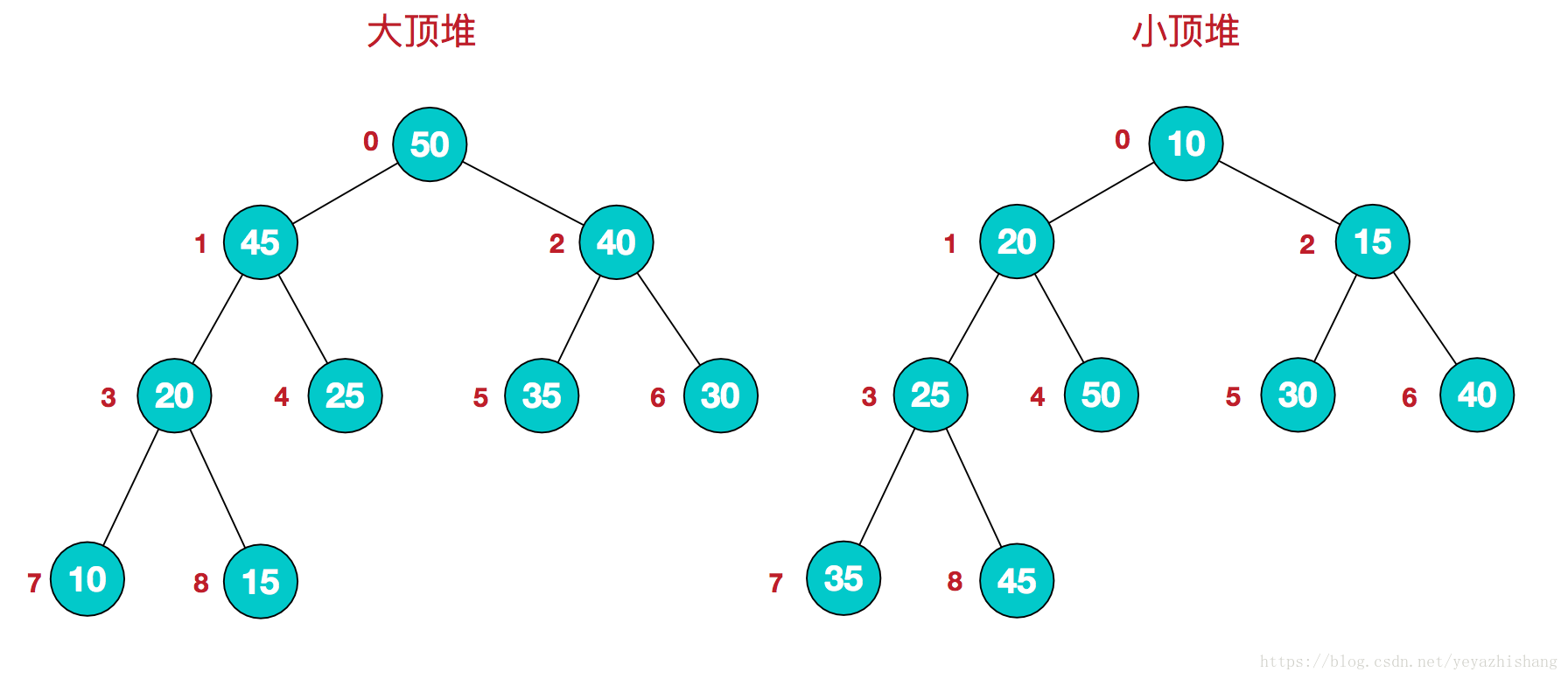
因为堆有序的特点,一般用来做数组中的排序,称为堆排序。
8.散列表
记录的存储位置=f(key)
这里的对应关系 f 成为散列函数,又称为哈希 (hash函数),而散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,这种存储空间可以充分利用数组的查找优势来查找元素,所以查找的速度很快。
哈希表在应用中也是比较常见的,就如Java中有些集合类就是借鉴了哈希原理构造的,例如HashMap,HashTable等,利用hash表的优势,对于集合的查找元素时非常方便的,然而,因为哈希表是基于数组衍生的数据结构,在添加删除元素方面是比较慢的,所以很多时候需要用到一种数组链表来做,也就是拉链法。拉链法是数组结合链表的一种结构,较早前的hashMap底层的存储就是采用这种结构,直到jdk1.8之后才换成了数组加红黑树的结构,其示例图如下: 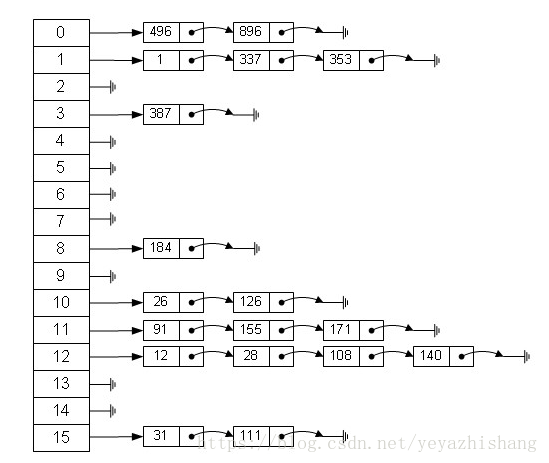
从图中可以看出,左边很明显是个数组,数组的每个成员包括一个指针,指向一个链表的头,当然这个链表可能为空,也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
哈希表的应用场景很多,当然也有很多问题要考虑,比如哈希冲突的问题,如果处理的不好会浪费大量的时间,导致应用崩溃。
文章内容摘抄于:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号