LCA详细讲解
LCA(Least Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。
———来自百度百科
例如:
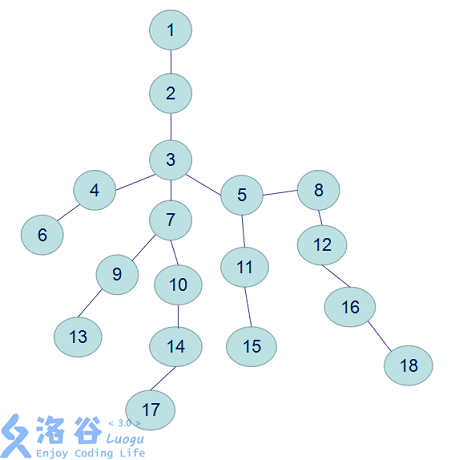
在这棵树中 \(17\) 和 \(8\) 的LCA就是 \(3\), \(9\) 和 \(7\) 的LCA就是 \(7\) 。
明白了LCA后,就下来我们就要探讨探讨LCA怎么求了 \(qwq\)
- 暴力算法
以 \(17\) 和 \(18\) 为例,既然要求LCA,那么我们就让他们一个一个向上爬(我要一步一步往上爬 —— 《蜗牛》),直到相遇为止。第一次相遇即是他们的LCA。
模拟一下就是:
\(17->14->10->7->3\)
\(18->16->12->8->5->3\)
最终结果就是 \(3\)
当然这个算法妥妥的会T飞掉,那么我们就要进行优化,于是就有了用倍增来加速的倍增LCA,这也是我们今天介绍的重点。
- 倍增算法
所谓倍增,就是按\(2\)的倍数来增大,也就是跳 \(1,2,4,8,16,32\) …… 不过在这我们不是按从小到大跳,而是从大向小跳,即按……\(32,16,8,4,2,1\)来跳,如果大的跳不过去,再把它调小。这是因为从小开始跳,可能会出现“悔棋”的现象。拿 \(5\) 为例,从小向大跳,\(5≠1+2+4\),所以我们还要回溯一步,然后才能得出\(5=1+4\);而从大向小跳,直接可以得出$5=4+$1。这也可以拿二进制为例,\(5(101)\),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
还是以 \(17\) 和 \(18\) 为例,如果分别从\(17\)和\(18\)跳到\(3\)的话,它们的路径分别是(此例只演示倍增,并不是倍增LCA算法的真正路径):
\(17->3\)
\(18->5->3\)
可以看出向上跳的次数大大减小。这个算法的时间复杂度为\(O(nlogn)\),已经可以满足大部分的需求。
想要实现这个算法,首先我们要记录各个点的深度和他们\(2^i\)级的的祖先,用数组\(\rm{depth}\)表示每个节点的深度,\(fa[i][j]\)表示节点\(i\)的\(2^j\)级祖先。
代码如下:
void dfs(int now, int fath) { //now表示当前节点,fath表示它的父亲节点
fa[now][0] = fath; depth[now] = depth[fath] + 1;
for(int i = 1; i <= lg[depth[now]]; ++i)
fa[now][i] = fa[fa[now][i-1]][i-1]; //这个转移可以说是算法的核心之一
//意思是now的2^i祖先等于now的2^(i-1)祖先的2^(i-1)祖先
//2^i = 2^(i-1) + 2^(i-1)
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
预处理完毕后,我们就可以去找它的LCA了,为了让它跑得快一些,我们可以加一个常数优化(来自洛谷提高组讲义)
for(int i = 1; i <= n; ++i) //预先算出log_2(i)+1的值,用的时候直接调用就可以了
lg[i] = lg[i-1] + (1 << lg[i-1] == i); //看不懂的可以手推一下
接下来就是倍增LCA了,我们先把两个点提到同一高度,再统一开始跳。
但我们在跳的时候不能直接跳到它们的LCA,因为这可能会误判,比如\(4\)和\(8\),在跳的时候,我们可能会认为\(1\)是它们的LCA,但\(1\)只是它们的祖先,它们的LCA其实是\(3\)。所以我们要跳到它们LCA的下面一层,比如\(4\)和\(8\),我们就跳到\(4\)和\(5\),然后输出它们的父节点,这样就不会误判了。
int LCA(int x, int y) {
if(depth[x] < depth[y]) //用数学语言来说就是:不妨设x的深度 >= y的深度
swap(x, y);
while(depth[x] > depth[y])
x = fa[x][lg[depth[x]-depth[y]] - 1]; //先跳到同一深度
if(x == y) //如果x是y的祖先,那他们的LCA肯定就是x了
return x;
for(int k = lg[depth[x]] - 1; k >= 0; --k) //不断向上跳(lg就是之前说的常数优化)
if(fa[x][k] != fa[y][k]) //因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。
x = fa[x][k], y = fa[y][k];
return fa[x][0]; //返回父节点
}
完整的求\(17\)和\(18\)的LCA的路径:
\(17->10->7->3\)
\(18->16->8->5->3\)
解释:首先,\(18\)要跳到和\(17\)深度相同,然后\(18\)和\(17\)一起向上跳,一直跳到LCA的下一层(\(17\)是\(7\),\(18\)是\(5\)),此时LCA就是它们的父亲
总体来说就是这样了,也不知道我这个蒟蒻讲的各位\(dalao\)能不能看明白
\(\tt{orz}\)
完整代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
struct zzz {
int t, nex;
}e[500010 << 1]; int head[500010], tot;
void add(int x, int y) {
e[++tot].t = y;
e[tot].nex = head[x];
head[x] = tot;
}
int depth[500001], fa[500001][22], lg[500001];
void dfs(int now, int fath) {
fa[now][0] = fath; depth[now] = depth[fath] + 1;
for(int i = 1; i <= lg[depth[now]]; ++i)
fa[now][i] = fa[fa[now][i-1]][i-1];
for(int i = head[now]; i; i = e[i].nex)
if(e[i].t != fath) dfs(e[i].t, now);
}
int LCA(int x, int y) {
if(depth[x] < depth[y]) swap(x, y);
while(depth[x] > depth[y])
x = fa[x][lg[depth[x]-depth[y]] - 1];
if(x == y) return x;
for(int k = lg[depth[x]] - 1; k >= 0; --k)
if(fa[x][k] != fa[y][k])
x = fa[x][k], y = fa[y][k];
return fa[x][0];
}
int main() {
int n, m, s; scanf("%d%d%d", &n, &m, &s);
for(int i = 1; i <= n-1; ++i) {
int x, y; scanf("%d%d", &x, &y);
add(x, y); add(y, x);
}
for(int i = 1; i <= n; ++i)
lg[i] = lg[i-1] + (1 << lg[i-1] == i);
dfs(s, 0);
for(int i = 1; i <= m; ++i) {
int x, y; scanf("%d%d",&x, &y);
printf("%d\n", LCA(x, y));
}
return 0;
}
- 广告
2019.10.21 upd:更改码风

