ALGO-19 方格取数

ALGO-19 方格取数

题目

资源限制

内存限制：256.0MB C/C++时间限制：1.0s Java 时间限制：3.0s Python 时间限制：5.0s

问题描述

设有 N×N 的方格图(N<=10),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 0。
某人从图的左上角的 A 点(1,1)出发，可以向下行走，也可以向右走，直到到达右下角的 B 点(N,N)。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 0）。
此人从 A 点到 B 点共走两次，试找出 2 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 N（表示 N×N 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 0 表示输入结束。

输出格式

只需输出一个整数，表示 2 条路径上取得的最大的和。

样例输入

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

样例输出

67= 21+15 + 13+14+4

代码

思路

很容易有一个动态规划的解法，令 \(dp[i][j]\) 表示到达\((i,j)\)的最大和，

\(dp[i][j]=max(dp[i-1][j],dp[i][j-1])\)，这是只走一次的状态转移方程

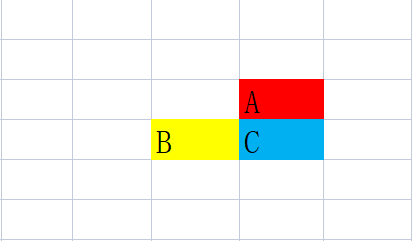
即\(dp[C]=max(dp[A],dp[B])\)然后再加值

如果是两次，就是可以认为是两个人同时走不同的路

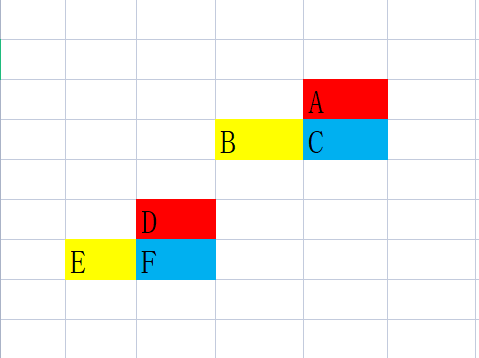
\(dp[C][F]=max(dp[C],dp[F])=max(dp[A],dp[B],dp[D],dp[E])\)

Java

import java.util.Scanner;

public class ALGO_19 {
    private static int[][] map;
    private static int[][][][] dp;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();
        int value;
        N++;// NOTE 这里是为了方便状态方程的计算
        map = new int[N][N];
        dp = new int[N][N][N][N];
        do {
            int row = scanner.nextInt();
            int col = scanner.nextInt();
            value = scanner.nextInt();
            map[row][col] = value;
        } while (value != 0);
        scanner.close();
        // NOTE 这里是因为N将要作为索引变量，所以要-1
        run(--N);
        System.out.println(dp[N][N][N][N]);
    }

    /**
     * 动态规划，尝试
     * @param {int} N
     */
    private static void run(int N) {
        for (int x1 = 1; x1 <= N; x1++)
            for (int y1 = 1; y1 <= N; y1++)
                for (int x2 = 1; x2 <= N; x2++)
                    for (int y2 = 1; y2 <= N; y2++) {
                        // NOTE 起点都从1开始也是为了状态方程的计算
                        dp[x1][y1][x2][y2] = Math.max(Math.max(dp[x1 - 1][y1][x2 - 1][y2], dp[x1 - 1][y1][x2][y2 -
                                1]), Math.max(dp[x1][y1 - 1][x2 - 1][y2],
                                        dp[x1][y1 - 1][x2][y2 -
                                                1]));
                        dp[x1][y1][x2][y2] += map[x1][y1];
                        if (x1 != x2 && y1 != y2) {
                            dp[x1][y1][x2][y2] += map[x2][y2];
                        }
                    }
    }
}