同态滤波（Homomorphic filtering）基本原理

同态滤波（Homomorphic filtering）基本原理

同态变换基本原理

同态变换一般是指将非线性组合信号通过某种变换，使其变成线性组合信号，从而可以更方便的运用线性操作对信号进行处理。

所谓非线性组合信号，举例来说，比如 z(t) = x(t) y(t)，两个信号相乘得到组合信号，由于时域相乘等价于频率域卷积，所以无法在频率域将其分开。但是我们应用一个log算子，对两边取对数，则有： log(z(t)) = log(x(t)) + log(y(t))，这样一来，就变成了线性组合的信号，log(x(t)) 和 log(y(t)) 时域相加，所以频域也是相加的关系，如果它们的频谱位置不同，就可以傅里叶变换后较好的分开，以便进行后续的分别的操作，比如应用高、低通滤波或者其他手工设计的滤波器等，然后再将结果傅里叶反变换，得到处理过的 \hat{ log(z(t)) }，在取幂，就可以得到最终的处理结果。

同态滤波的应用

图像中的同态滤波

在图像处理中，常常遇到动态范围很大但是暗区的细节又不清楚的现象，我们希望增强暗区细节的同时不损失亮区细节，一般来说，我们可以将图像f(x,y)建模成 照射强度（illumination） i(x,y) 和 反射强度（reflection） r(x,y)的乘积，所以有：

f(x,y)=i(x,y)r(x,y)$$f(x,y)=i(x,y)r(x,y)$$

一般来说，自然图片的光照一般是均匀渐变的，所以i应该是低频分量，而不同物体对光的反射是具有突变的，所以r是高频分量。现在我们对两边取对数，并做Fourier变换，得到线性组合的频率域。

lnf(x,y)=lni(x,y)+lnr(x,y)$$\ln f(x,y)=\ln i(x,y)+\ln r(x,y)$$

FFT(lnf(x,y))=FFT(lni(x,y))+FFT(lnr(x,y))$$FFT(\ln f(x,y))=FFT(\ln i(x,y))+FFT(\ln r(x,y))$$

我们希望对低频能量进行压制，这样就降低了动态范围，而要对高频进行提高，这样就增强了图像的对比度，示意图如下：

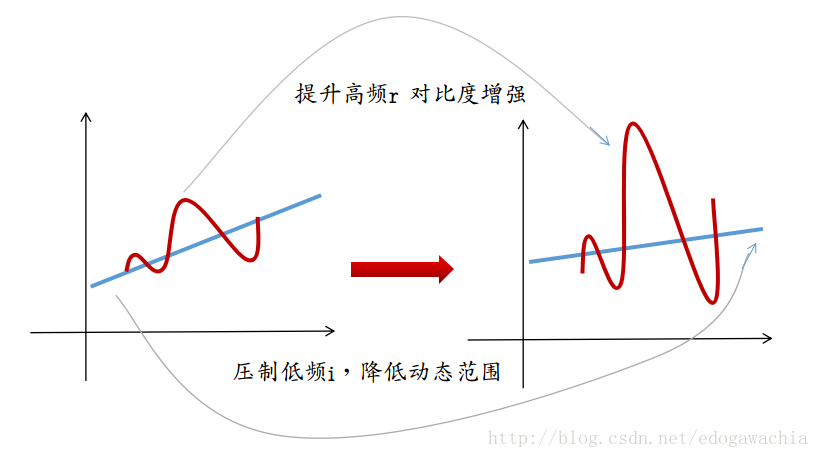
所以采用的滤波器为：

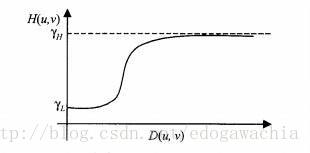
操作完成后在按照之前介绍的步骤，反变换，求幂，即可得到处理后的图像，整个过程的流程图如下：

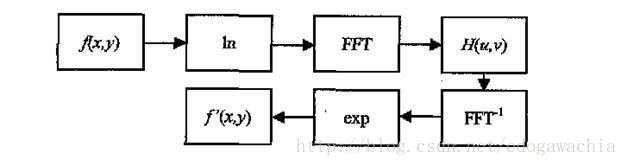
地震子波求取

从地震道中提取地震子波，考虑到地震道数据y是由子波b和反射系数r褶积得到的，因此无法直接分离。

那么考虑到时域的褶积就是频域的乘积，在频域应用log对数，进行同态变换，就可以将两者分开。如果假设反射系数是白噪声形式，那么由于子波是wavelet的形式，在频域只集中于0附近。将同态变换后的信号反变换回时域，做低通滤波就可以将子波对应的部分提取出来，然后再回到频域求幂，再反变换回来即可得到地震子波的时域信号，具体流程如下：

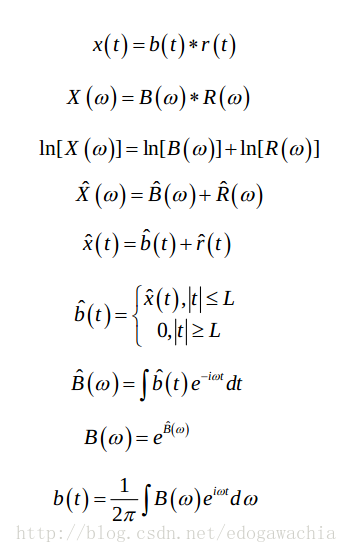
2018年02月25日14:40:43

笨蛋才思考，聪明人用灵感，我们大多时间都是笨蛋，偶尔才成为聪明人。 —— 导演，斯坦利 库布里克