classical CNN models : LeNet-5 模型结构详解
LeNet - 5
相关文献:
Gradient-Based Learning Applied to Document Recognition
YANN LECUN, MEMBER, IEEE, LÉON BOTTOU, YOSHUA BENGIO, AND PATRICK HAFFNER
PROCEEDINGS OF THE IEEE, VOL. 86, NO. 11, NOVEMBER 1998
网络结构
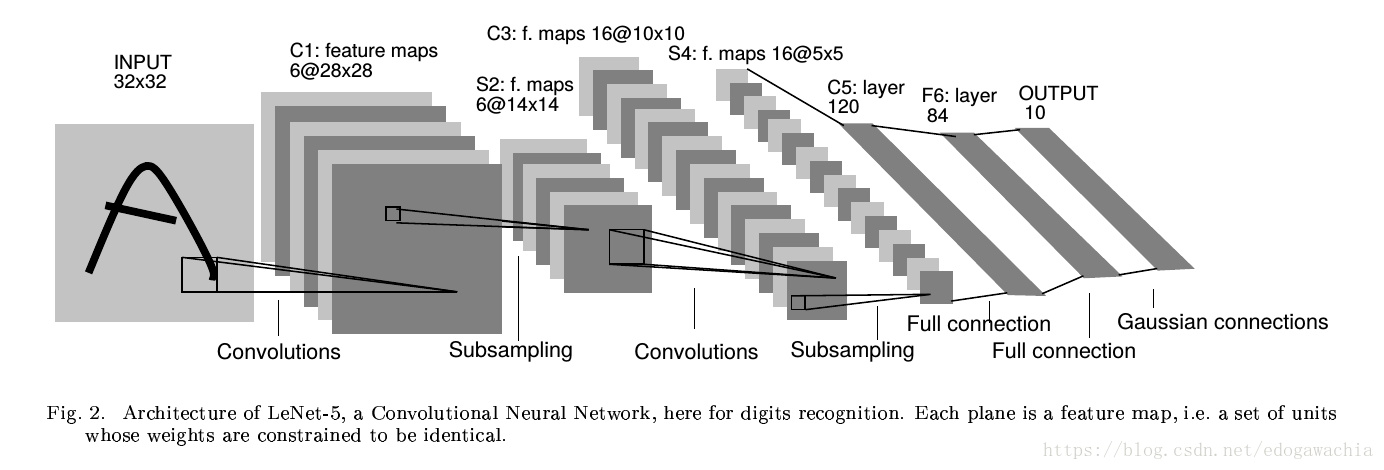
在文章的比较环节里面还给出了其他的lenet,比如lenet-1,lenet-4等,但是最常见的还是上面这种lenet,也就是LeNet-5。
这个网络是最早的具有现在的CNN的基本环节和框架的卷积神经网络。可以看出,LeNet-5包含如下一些技术:
- 权值共享,也就是卷积的kernel来代替全连接,从而减少参数规模的方法。
- subsampling,降采样,实际上也就是池化pooling操作。
- 用RBF,径向基函数,来作为loss函数进行训练,已经有了很像图像分类的损失函数了。
- 在convolution层之后做全连接FC层,使得网络符合:卷积-池化-全连接 的基本形式,后来的ImageNet比赛中胜出的的各种CNN,如alexnet,vgg等基本都是这种采用了这种模式。
下面按照网络的层顺序说明其结构:
该网络目的是手写字母或者数字,如邮编,的识别问题,实际上就是一个已知所有字符模式的一个匹配,或者分类的问题。因为从MNIST上测试,也就是说,图片输入大小为28×28,这里首先把输入做成32×32,把28的图像放在中间,目的是在第一层做5×5的convolution提取特征的时候,边角的位置的特征也能被提取到,因为一次5×5过后,32就变成了28(也就是现在常说的convolution的mode中full,same,valid的valid模式)。然后得到了6个28×28的feature map,对这些fm也就是C1层做降采样,这里的降采样和max pooling等不太一样,它的做法是这样:采样后的fm的每个像素都只和上面的2×2的邻域有关,首先把对应于S2中一个unit 的四个input相加,然后给它们乘上一个可以训练的系数,再加上bias,然后过一个sigmoidal的激励函数。2×2的receptive field是不重叠的,这和pooling是一致的。这样就得到了14×14的6个fm,也就是S2。然后对S2再做convolution,仍然是5×5,但是这里需要注意,C3中的每个fm不是和S2中所有的fm都有连接的。(现在的CNN都是后面和前面卷积层所有的fm都有连接)。其连接方式如下图:
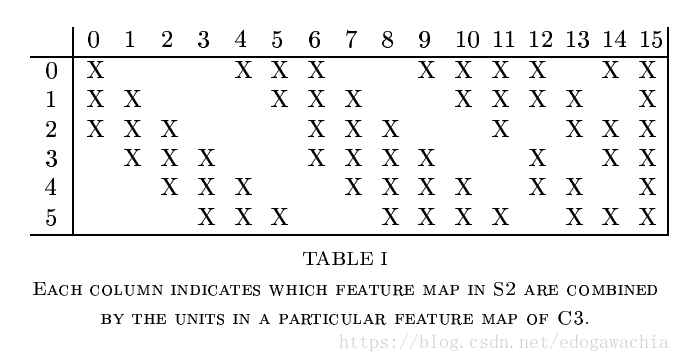
column对应的是上一层的6个,row对应于下一层的16个。可以看出,这16个里,前面的6个,即0–5,是由相邻的三个fm组合变换而成,而中间的6个,即6-11,是相邻的四个fm,而再后面的三个是不相邻的四个fm,最后一个,即15,是所有的fm都连接得到的。
为何要采用这样的连接。作者给出两点理由:首先,可以降低连接数目(毕竟当时还没有这么多框架和GPU,参数量规模不要过大还是一个需要考虑的因素);另外,更重要的一个理由是,作者希望通过这种方式学得一个可以互补的fm,通过强行破坏网络结构中,也就是上下层连接中的这种对称性。
这样可以得到C3。对C3进行一个降采样,方法同上,得到S4,16个5×5的fm,然后在进行一个5×5的卷积,得到C5,由于是valid,所以C5已经变成了1×1的fm图像,也就是已经变成了scalar。而且变成了120个fm,这里的120个每个都和前面的16个相连,没有之前6到16的那种方式。这里还把该层看成是C5,也就是第5个卷积层。(lenet-5的5就是表示它有5个convolution层)当然也可以认为这是一个FC。之所以不叫FC是因为这里的输入是32,刚好在该层变成了1×1,如果换别的数据,那么就不是scalar而仍是fm了。然后过了一个F6,成了84的全连接。这里之所以要用84,是因为每个待识别的label都用一个模式来表征,这个模式就是7×12的bitmap,(如下图),所以为了和这些stylized image匹配,所以设定为84。

最后一层用欧式径向基函数,ERBF,来计算和每一个类别的距离,距离越近输出越小,也就是说明越接近某个模式。
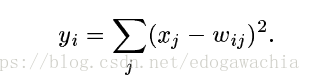
这样用模式图匹配在数字上看不太出优势,但是在ascii码上就比较明显,因为有很多confusable的比如:O,o,0,或者小写的l和数字1。这时候用匹配就有用了。
一直到F6层,所有的激活函数都是sigmoid squashing function,也就是tanh函数,双曲正切:

2018年04月16日16:10:38
昨天,准备了今天的颠倒疯狂;酝酿了明天的沉默凯旋绝望;喝吧,你又不知从何来为何来;喝吧,你又不知因何去去何方。 —— 诗人 奥马尔 哈亚姆

