机器学习中的各种损失函数（Hinge loss，交叉熵，softmax）

机器学习中的各种损失函数

SVM multiclass loss（Hinge loss）

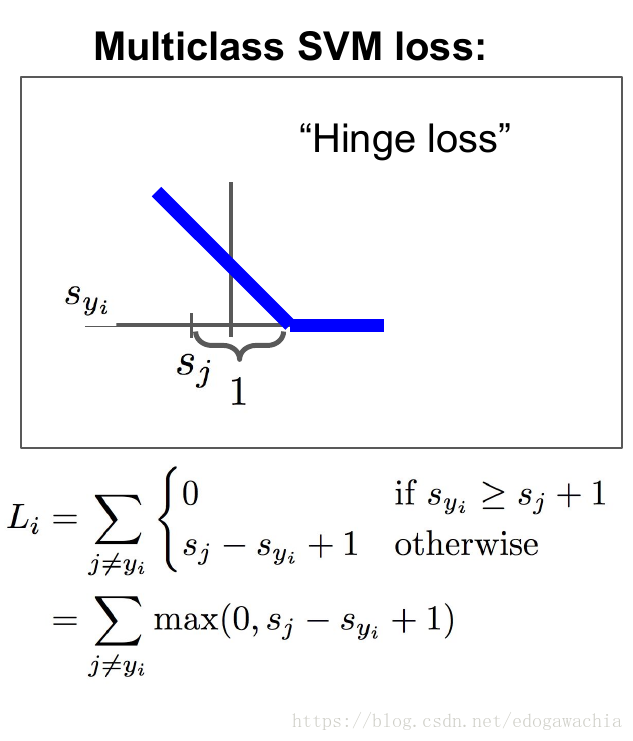
这是一个合页函数，也叫Hinge function，loss 函数反映的是我们对于当前分类结果的不满意程度。在这里，多分类的SVM，我们的损失函数的含义是这样的：对于当前的一组分数，对应于不同的类别，我们希望属于真实类别的那个分数比其他的类别的分数要高，并且最好要高出一个margin，这样才是安全的。反映在这个函数中，就是0的那一项的取值范围，Syi表示的是xi样本的真实类别所得到的分数，而Sj指的是其他的类别的分数，如果真实类别的分数是最大的，且大一个margin 1，那么就表示满意，也就是说不惩罚，这一项的loss为0。如果不满足这一条件，我们用下面的一段，也就是Sj - Syi + 1, 1在这里是一个常数，可以使得函数连续起来，这个Sj - Syi表示，Syi，也就是真实样本的分数比别的少的越多，我们越不满意，具体计算方式有下面这个栗子：

有时候我们也会用hinge function的平方项作为loss函数。

考虑到很多W都能满足零loss，那么如何在这些W中做出选择？

这里就需要对W进行选择，也就是正则，引出了经验风险损失和结构风险损失的概念，正则的概念众所周知，此略。

这里乱入一下各种正则化，关于正则化的相关问题留作以后整理。

multinomial logistic regression （softmax loss）

就是常说的softmax的损失函数，通过将score变成probablity，从而每次只用计算属于正确的分类的那个概率，用对数最大似然的方法，将它变成prob == 1，也就是min -log 使其等于0 。

可以看出，如果类别标签是one-hot vector的话，那么实际上只对真实类别的一类进行求log并加负号。

但是，考虑到这一类的prob是由所有的logits的exp后的和归一化得来的，因此实际上还是对所有的score都有作用。相对于前面的SVM的hinge loss，可以这样对比描述：Hinge loss 对于那些对真实类别给分高的样本不进行过多奖励(loss小相当于奖励高)，也就是说只要正确类别的分数比其他的大1以上，那么就认为这个score已经足够好了，这样就可以关注整体的loss，争取所有样本上表现都比较好。而softmax loss 是对概率分布进行优化，力图使所有的概率密度都向着正确分类样本上集中。

* 关于多分类问题的 softmax loss 和 二分类问题的 logistic 回归的 loss

二分类问题的logistic回归的loss函数是：

loss=−1n∑[ylna+(1−y)ln(1−a)]$$loss=-\frac{1}{n}\sum [y\ln a+(1-y)\ln (1-a)]$$

可以看出，二类别的分类是多分类的一个特殊情况，因此也可以用softmax的方式来处理。但是二分类又是一个特例，因为它的类别不用写成one-hot vector，而是直接用0到1之间的一个数字就可以表示，接近1就是正例，接近0就是反例。所以符合上面的这个公式。这个公式可以看出，y=0，即真实标签为0的时候，第一项就没有了，loss变成-(1-y)ln(1-a)，也就是-ln(1-a)，a越接近0，loss越小；y=1时反之，这样就使得a越来越趋近于真实答案。

考虑到a是logistic方程的输出，x为输入，w是要优化的weights，a在0-1之间，如果我们把两个类别按照多分类的方式，写成one-hot vector的话，那么可以是[1, 0] 和 [0 ,1] ，那么用softmax输出的结果分别是[1-a, a]，其中a接近0，这个向量就接近[1,0]也就是第一类，a接近1，向量接近第二类。用softmax写出来，就和上面的logistic二分类的loss一样了。

logistic回归的loss是可以通过最大似然取对数写出来的，这里假设样本的label，也就是类别服从Bernoulli分布。在【统计学习方法（李航）】一书中有推导过程，如下：

交叉熵损失函数（cross entropy loss function）

交叉熵的公式：

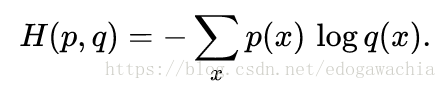
这个是来源于信息论的一个定义，表示的是用某个分布去编码另一个分布所需要的平均码长。

作为损失函数时，它可以用来度量两个分布的差异性，比如上述的 softmax 得到的概率分布，和one-hot的概率分布相比，差异性就可以用cross entropy来衡量。按照编码的规则，作为权重的p和在log里面的p两个分布分别代表着真实分布和用来编码的预测分布，这个函数越小，说明两个分布越相像。

用交叉熵损失函数的优势在于，可以避免MSE损失带来的梯度过小的问题。（mse求导后chain里面带着sigmoid的导数，这个导数在有的位置是接近于0的，也就是前面说的软饱和，而cross entropy的导数只和真实值和预测值的差异成正比，所以避免了这一问题。）

2018年04月23日16:49:40

人间永远有秦火烧不尽的诗书，法钵罩不住的柔情。 —— 散文家，张晓风 【风荷举】