l1-norm loss & l2-norm loss (l1范数和l2范数作为正则项的比较)
l1-norm loss & l2-norm loss (l1范数和l2范数作为正则项的比较)
l1-norm 和 l2-norm是常见的模型优化过程中的正则化项,对应到线性回归的领域分别为lasso Regression和 Ridge Regression,也就是 lasso 回归(有的地方也叫套索回归)和岭回归(也叫脊回归)。在深度学习领域也用l1和l2范数做正则化处理。这里简要介绍一下lasso和ridge(Ridge相关详见另一篇笔记:【https://blog.csdn.net/edogawachia/article/details/79478266】),以及l1-norm和l2-norm做正则化对最终的解的影响(为何l1偏向于稀疏解)。另外,l1范数的下降方法留作下一篇整理。
Lasso Regression和 Ridge Regression
lasso 的全程是 least absolute shrinkage and selection operator,也就是最小绝对值收缩和选择算子。lasso的公式如下:
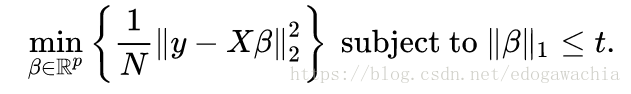
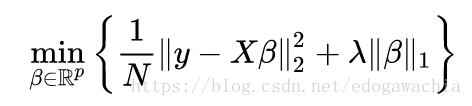
上面两种表示是同一个问题,也就是在l1norm正则下优化线性回归问题,这里下面的写法是上面的写法的lagrangian form。
下面是ridge Regression:
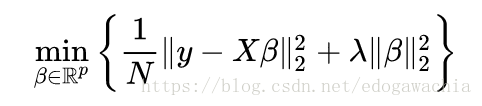
可以看出,是用l2 norm做正则,其他和上面相同。
另外,还有一种正则方式,或者叫做特征选择方式,叫做best subset selection,最优子集选择,它等价于对下面这个式子的minimization,也就是以0范数做正则进行优化。
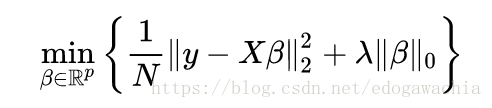
下面贴一个很好的ppt中的解释,链接在文末。


l1-norm 和 l2-norm
先总结一下l1和l2 norm
- l1 norm更倾向于稀疏解。
- l1 norm 对于离群点更加鲁棒。
- l1 norm 对应拉普拉斯先验,l2 norm对应高斯先验。
首先看一下各种lp norm的形状:
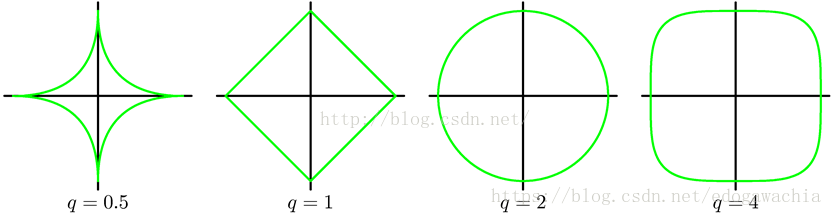
从0到inf,norm的形状是逐渐变“胖”的过程,当然这是有限度的,限制就是l inf norm时候的立方体,可以看成一个初始在坐标轴上逐渐膨胀的气球被禁锢在一个在各坐标轴为1的点处与该轴垂直的平面所围成的一个盒子里。如图所示,0范数就是非零元素的个数,具体的值不考虑,1范数是绝对值,2范数是一个单位球形状。而且,所有小于1的norm都是不凸的,l1是最小的凸函数。
通常对w用l1做正则的时候是希望它可以把w做成稀疏的,也就是我们可以对很多特征的系数置0,也就是起到特征选择的作用。那么用l0 norm显然是最合适的,但是由于l0范数不凸,所以我们对它进行凸松弛,而l1范数这时就出现了,因为它是和l0范数最接近的凸近似,所以通常用l1范数也能得到稀疏解。
稀疏
l1-norm 为何可以得到稀疏解,可以用以下图说明:
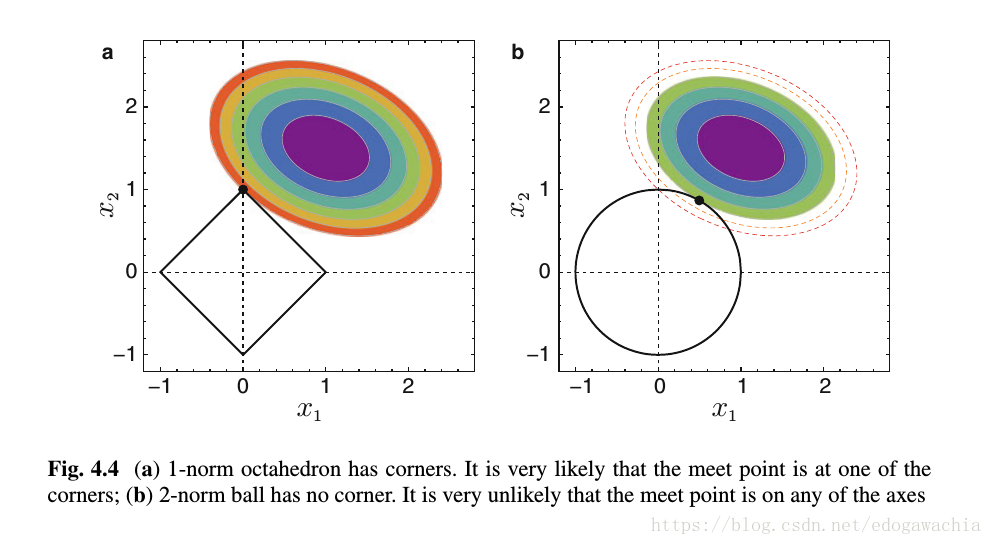
图片来自于李力老师的凸优化及其应用一书中的截图。为了和图相对应,首先将带有正则的函数写成优化线性表示和真实答案的差值的约束优化问题,其中subject to |w| < c 或者|w|_2 < c。这里可以看出,右上角是要优化的函数的等值线,而圆形和菱形就是2范数和1范数的约束,可以看到,1范数相对于2范数,在坐标轴以外的凸出的表面积(这里是线段长度)更小,也就是说,相对于2范数,1范数和待优化的函数的等值面更容易交于坐标轴,而2范数更偏向于非坐标轴。(沿着这个思路继续想下去,l0范数只在坐标轴有值,因此肯定是稀疏的,而0-1之间的范数虽然表面积大一些,但是并不是凸出去的表面积,因此和我们要优化的凸函数并不能更早的相交)。这也就是为什么在特征选择和希望得到稀疏解的时候选择1范数的理由。
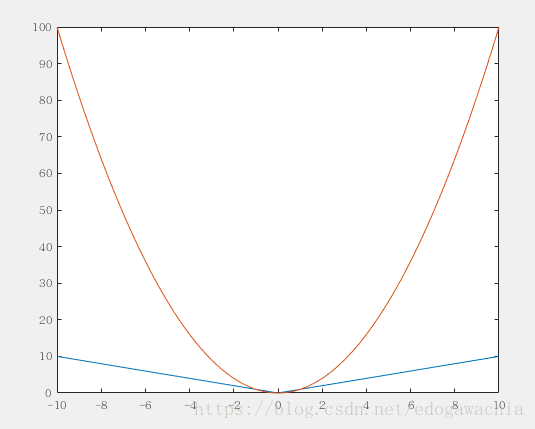
也可以这样考虑,对于l1范数的绝对值函数 f(x) = |x|,和l2范数的f(x) = x^2, 可以对比函数图像,在下降过程中,绝对值函数是自变量下降多少,函数值就下降多少;而二次函数的函数值下降的是自变量的平方,当自变量下降到0附近时,自变量的变化引起的范数减小值不明显,因此也就不容易得到0,也就不容易得到稀疏解。
鲁棒
由于l2范数对距离0较远的值(离群点或野值)惩罚较大,因此会更加关注到这些点。但是往往这些野值点是由于采集数据的失误等造成的,是无参考价值的。这样一来,l2norm下的回归得到的结果就会受到野值的影响,偏移其他正常点表示的位置。而l1对野值不敏感,因此可以更鲁棒的回归。
Bayesian view : 先验分布


由上面的图很容易能看出来,Gaussian的指数是关于w的一个平方项,Laplacian是一个绝对值项。
实际上,从贝叶斯的角度看,我们对优化模型的正则实际上就是加入了先验知识。实际上也确是如此,为何我们偏向简单模型,特别是w的能量较小的,不管以什么方式,l1也好l2也好,或者其他的比如max norm,为何我们希望结构风险最小化?这个结构风险指的究竟是什么?实际上,这里我们已经人为地预设了一个假设:实际有效的模型都是简单的,也就是所谓的occam razor 奥卡姆剃刀原则(btw,这个经院哲学家的一条格言在机器学习还有信息论里面都备受青睐)。这个就是我们的先验知识,反映到模型中就是正则项。但是这个经验只是需要w较小,也就是集中在0附近最好,但是具体如何集中没有表明,因此用Gaussian和laplacian都是合理的。

(上面就是奥卡姆的威廉,奥卡姆剃刀的作者)
由贝叶斯定理可以知道,我们的先验和似然通过乘积的方式,即可得到后验概率(当然要做边际化,或者叫归一化)。为了方面求解,我们取对数,变成相加的形式,似然函数就是我们的经验风险最小化的一项,也就是拟合样本的一部分;而后面的另一个加数就是先验取对数,就是我们的正则。再回到上面两页ppt中的公式,可以看到,取了对数以后,就把指数项拿下来了,就变成了l1和l2 norm,因此就说明了l1和l2分别与Gaussian和laplacian的对应性。
reference:
http://www.unicog.org/pmwiki/uploads/Main/PresentationMM_02_10.pdf
2018年04月23日23:19:49



