【NLP模型笔记】GloVe模型简介
GloVe模型

glove模型的参考资料链接如下:
https://nlp.stanford.edu/projects/glove/
论文链接(pdf)如下:
https://nlp.stanford.edu/pubs/glove.pdf
GloVe: Global Vectors for Word Representation [Jeffrey Pennington], [Richard Socher], [Christopher D. Manning]
GloVe的基本思路
和之前讲过的word2vec(SG和CBOW)一样,glove模型也是一种无监督的词嵌入方法,即词向量学习方法。
glove是一个全局对数双线性回归模型(global log bilinear regression model)。顾名思义,该模型用到了语料库的全局特征,即单词的共现频次矩阵,并且,其优化目标函数是对数线性的,并用回归的形式进行求解。
glove的思想基于这样一个经验,如下图所示:

在glove的论文中,作者举了上表中的这样一个栗子。现在我们已经知道ice和steam这两个词在语料中出现的频率,这两个词被视为目标词(target words) ,也就是需要对它们的词向量进行学习和表征的词语。此时,我们暂且不直接去求解这两个词之间的共现关系(就像word2vec那样),而是基于这两个词的频率,去探索一下given这两个目标词的情况下,其他词的条件概率是一个什么情况,这里的k就是其他词。
首先,我们计算given单词ice的情况下,单词k出现的频率,也就是说,k出现在i的上下文中的概率是多少。这个条件概率记做P(k|ice),P(k|ice) = X k,ice / X ice,X k, ice是k和ice在同一个context中出现的次数,X ice为ice出现的次数。同理,我们计算P(k|steam),计算方法一样。这里的k可以是字典中的任何一个单词。
下面,我们观察两个条件概率的比值,也就是对于任一个k,k出现在ice的context中的条件概率,与k出现在steam的context中的条件概率,这两者之间的比值。
上面表格中,作者展示了k取solid,gas,water,fashion这四个值的时候,比值的情况。为啥要取这四个值呢?因为solid和ice语义上是有关的,冰是固体嘛,而solid和steam没有语义的关系;而gas则相反,与steam有语义关系,与ice则无;而water则与ice和steam两者都有关系,一个是水汽,一个是水的固态,即冰;而fashion这个词明显与ice和steam都无关。作者计算了这四个k下的条件概率比值,我们发现,当k与分子上的这个词(ice)接近,而与分母(steam)无关时,这个比值远大于1,而k与分母更接近,则比值远小于1。另外两种情况,要么k与分子分母都有关,要么都无关,这时候,这个比值基本在1附近,表明这两个条件概率其实差不太多。这样一个结论也是符合我们的直觉的。毕竟语义相近,出现在上下文中的比例更高一些嘛,也是合理的。
而正是基于这个朴素的道理,glove的作者决定用一个函数去拟合这个条件概率的比值,即:
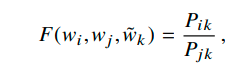
其中,i和j就是目标词,k就是用于计算条件概率的上面讲的那个k。拟合ratios of co-occurence probability这个思路是glove中最基本和最重要的。我们来稍微详细讨论一下这个问题。首先,对于词嵌入这个任务来说,我们的目标是让语义相同的词语在向量空间中离得更近一些,因此,我们首先得需要找到在实际的语料中(而非向量空间中)如何数学化地表达两个词语的相似程度。word2vec对这个问题的答案是在context中出现的概率。这个思路自然是对的,但是这种embedding方法相当于绝对地去模拟两个词之间的条件概率。而我们知道,对于人类的自然语言来说,每个单词的意义实际上是建构在词语之间的结构当中的。换句话说,每个词语只有当与其他词语比较时才真正能有其意义。比如NLP中常举例的一个栗子:king - man + woman = queen,这个analogy中,我们其实并不需要实际地知道king和man等词语在实际的世界中所指称的对象(很多抽象概念甚至没有实际指称的经验对象),而是只需要知道这几个词之间的逻辑关系即可。因此,相比起绝对地描述一个词语,通过与第三者的比较,得到第三者与两个词语中的哪个更接近这样一个相对的关系,来表达词语的含义,实际上更符合我们对于语言的认知。很容易联想到的是,这样一来,我们学习出的vector在analogy这个任务上可以被期待做的更好,因为用词向量拟合这个条件概率ratio,本身就是基于两个词向量相对于另外的其他词向量之间关系来做的。所以,作者在abstract中说道:这样学习出来的vector space具有一个meaningful substructure。这个比值关系是glove最基本的思路,理解了这一点,我们下面来看怎么样通过上面这个式子推导出glove的损失函数。
首先,上面的F这个函数是个三元函数,包括了wi,wj,tilde wk。这个F由于拟合的是条件概率的比值,也就是k与i和j的相似性,因此它应该是个相似性的度量。考虑到在vector space中,我们希望词向量之间的关系是linear的(正如前面的king-man+woman=queen的例子),因此,我们将我们的目标词i和j的向量相减,让这个F只和wi-wj有关,即:
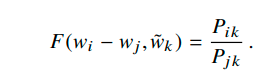
这样,只需要计算wk和wi-wj之间的相似度,就可以拟合右边的ratio了。到这里,其实不难发现,由于k要与i和j比较,看看与i,j中哪一个更近,因此这个wi-wj 和wk的关系可以用向量点积(内积)来处理,因为向量内积表示相似度,这样一来,wiTwk表示i和k的相似度,wjTwk为j和k的相似度,如果k和i更接近,则减号前的大,否则减号后的大。
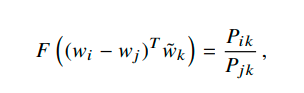
这里,我们发现,如果把i和j换换位置,得到F( (wj-wi)T wk) = Pjk / Pik,和上式相比,我们发现F函数有一个性质,那就是F(x) = 1/ F(-x) 。具备高中数学函数知识就可以猜到,这个F就是一个exp()指数函数。exp(-x) = 1/exp(x)。(这一段内容为了容易理解,与论文中说明方法略有不同)
这样,我们带入指数函数,与Pik和Pjk对应后发现,exp(wiTwk) = Pik,因此,可以得到:
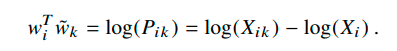
这里我们把Pik = Xik / Xi这个除法通过log拆成了减法。
由于右边有一个log(Xi),我们这个式子不对称了。试想一下,如果把wiTwk换成wkTwi,那么右边需要 -log(Xi)呢还是 -log(Xk)呢?为了维持这种对称性,我们把-log(Xi)丢掉,但是由于这个term之和i有关,因此可以在左边加一个bi作为i的bias。为了维护对称性,我们只好也对k加一个同样的bias,于是得到:
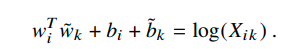
到这里,我们就已经基本结束了 ,因为我们知道了word vector要拟合的目标。下面就是一些技术性的trick了:

上面的 J 就是最终的loss function。里面有一个f函数,作为加权项。这个函数的设计很有意思,它的性质在上面的1 2 3中已经说明了。下面看一下它的图像:

可以看到,这个函数以Xij为自变量,在取值小的区间递增,而大于某个thr后,即xmax,就开始不再增加。Xij过高的那些word的权重相对就被压下来了。这就意味着,那些高频词组合对模型的影响相对小一些,从而使得那些出现不那么多的词语的co-occurence有机会更多地影响和改变模型。这个思路主要是由于自然语言中天然的长尾效应,为了使得长尾部分不至于被头部掩盖掉,只好通过赋权的方式降低这两个部分在loss中占比的差异。这个想法和自然语言处理中先去停用词(stop-words)的思路是类似的。
以上就是GloVe的基本原理和推导过程。
.
…
…
2020年4月28日01:55:58
北京
春将归去,与汝同车,低声细语。
—— 【日】 松尾芭蕉



