4.28(TG模拟赛)总结
1.挖地雷
题目背景
NOIp1996提高组第三题
题目描述
在一个地图上有N个地窖(N≤20),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
输入输出格式
输入格式:
有若干行。
第1行只有一个数字,表示地窖的个数N。
第2行有N个数,分别表示每个地窖中的地雷个数。
第3行至第N+1行表示地窖之间的连接情况:
第3行有n-1个数(0或1),表示第一个地窖至第2个、第3个、…、第n个地窖有否路径连接。如第3行为011000…0,则表示第1个地窖至第2个地窖有路径,至第3个地窖有路径,至第4个地窖、第5个、…、第n个地窖没有路径。
第4行有n−2个数,表示第二个地窖至第3个、第4个、…、第n个地窖有否路径连接。
… …
第n+1行有1个数,表示第n−1个地窖至第n个地窖有否路径连接。(为0表示没有路径,为1表示有路径)。
输出格式:
有两行
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
输入输出样例:
输入样例#1:
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
输出样例#1:
1 3 4 5
27
开始犯傻:
说实在的,考前,刚好打了一半这道题的dfs,但是考试之后打怎么也不对,于是打了个一本通的dp,我好LJ。
(1)dfs的心里路程就是定义一个bool型函数判断它还能不能挖,dfs函数部分判断如果不能继续挖下去,并且挖到的地雷数比之前的还多,就用opt记录路径pre,如果还能挖下去,就for循环找下一个能挖的地方,然后b改变标记,继续dfs,注意回溯b的标记。(码风可能有些奇怪
#include"bits/stdc++.h"
using namespace std;
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int n;
int ans=0;
#define N 22
int a[N];
int mp[N][N];
#define INF 0x3f3f3f3f
int pre[N];
bool b[N];
int cnt;
int opt[N];
int print(int x) {
if(!pre[x]) cout<<pre[x]<<' ';
else print(pre[x]);
}
bool check(int x) {
for(int i=1; i<=n; i++)
if(mp[x][i] && !b[i]) return false;
return true;
}
void dfs(int x,int step,int sum) {
if(check(x)) {
if(sum>ans) {
ans=sum;
cnt=step;
for(int i=1; i<=step; i++)
opt[i]=pre[i];
}
return ;
}
for(int i=1; i<=n; i++) {
if(!b[i] && mp[x][i]) {
b[i]=1;
pre[step+1]=i;
dfs(i,step+1,sum+a[i]);
b[i]=0;
}
}
}
void init() {
for(int i=1; i<=n; i++) pre[i]=0;
for(int i=1; i<=n; i++) b[i]=false;
}
int main() {
n=read();
init();
for(int i=1; i<=n; i++) a[i]=read();
for(int i=1; i<=n-1; i++) {
for(int j=i+1; j<=n; j++) {
cin>>mp[i][j];
}
}
for(int i=1; i<=n; i++) {
b[i]=1;
pre[1]=i;
dfs(i,1,a[i]);
b[i]=0;
}
for(int i=1; i<=cnt; i++)
cout<<opt[i]<<' ';
cout<<endl<<ans;
return 0;
}
(2)dp的心里路程是逆推,状态转移方程是f[i]=max{f[j]+h[i]}(mp[i][j]=1,i<j<=n)。
#include<stack>
#include<queue>
#include<algorithm>
#include<cmath>
#include<set>
#include<map>
#include<cctype>
#include<list>
#include<iostream>
#include<cstdio>
#include<cstring>
#define N 222
using namespace std;
int n;
int mp[N][N];
int h[N];
int f[N];
int ans=0;
int k=0;
int a[N];
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int main() {
/* freopen("lei.in","r",stdin);
freopen("lei.out","w",stdout);*/
n=read();
for(int i=1; i<=n; i++) cin>>h[i],f[i]=h[i];
int x,y;
/* while(scanf("%d",&x)!=0&&scanf("%d",&y)!=0) {
mp[x][y]=1;
}*/
for(int i=1; i<=n; i++)
for(int j=i+1; j<=n; j++) {
int ww;
cin>>ww;
if(ww==1)
mp[i][j]=1;
}
a[n]=0;
for(int i=n-1; i>0; i--)
for(int j=i+1; j<=n; j++)
if(mp[i][j]&&f[j]+h[i]>f[i]) {
f[i]=f[j]+h[i];
a[i]=j;
}
for(int i=1; i<=n; i++)
if(ans<f[i]) {
ans=f[i];
k=i;
}
cout<<k;
k=a[k];
while(k) {
cout<<" "<<k;
k=a[k];
}
cout<<"\n"<<ans<<'\n';
return 0;
}
(有木有感觉我的代码很眼熟,是的,它就是一本通的嘿嘿Q
2.跳石头
题目背景
一年一度的“跳石头”比赛又要开始了!
题目描述
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走 M 块岩石(不能移走起点和终点的岩石)。
输入输出格式
输入格式:
第一行包含三个整数L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。保证 \(L \geq 1\) 且 \(N \geq M \geq 0\)。
接下来 N 行,每行一个整数,第 i 行的整数\(D_i( 0 < D_i < L)\), 表示第i块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出格式:
一个整数,即最短跳跃距离的最大值。
输入输出样例:
输入样例#1:
25 5 2
2
11
14
17
21
输出样例#1:
4
说明:
输入输出样例1说明:将与起点距离为2和14的两个岩石移走后,最短的跳跃距离为 4(从与起点距离17的岩石跳到距离21的岩石,或者从距离21的岩石跳到终点)。
另:对于20%的数据,0 ≤ M ≤ N ≤ 10。
对于50%的数据,0 ≤ M ≤ N ≤ 100。
对于100%的数据,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
开始犯傻:
这道题用到了小a学长讲的二分答案。
于是,在这里献丑啦。总结一下二分答案:
- 求最大的最小值
- 求最小的最大值
- 求满足条件下的最大(最小)值
- 求最靠近一个值的值
- 求最小的能满足条件的代价
附上一个接近万能的二分模板:
int erfen(int x){
int l=1,r=maxn,ans=0;
while(l<=r){
int mid=(l+r) >> 1;
if(check(mid)) ans=mid,l=mid+1;
else r=mid-1;
}
return ans;
}
再附上一位dalao的讲解:
二分答案应该是在一个单调闭区间上进行的。也就是说,二分答案最后得到的答案应该是一个确定值,而不是像搜索那样会出现多解。二分一般用来解决最优解问题。刚才我们说单调性,那么这个单调性应该体现在哪里呢?
可以这样想,在一个区间上,有很多数,这些数可能是我们这些问题的解,换句话说,这里有很多不合法的解,也有很多合法的解。我们只考虑合法解,并称之为可行解。考虑所有可行解,我们肯定是要从这些可行解中找到一个最好的作为我们的答案, 这个答案我们称之为最优解。
最优解一定可行,但可行解不一定最优。我们假设整个序列具有单调性,且一个数x为可行解,那么一般的,所有的x'(x'<x)都是可行解。并且,如果有一个数y是非法解,那么一般的,所有的y'(y'>y)都是非法解。
接下来code就很好搞啦~
值得注意的一点是,它终点也是有石头的~
check函数判断,详见代码啦~
#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<queue>
#include<algorithm>
#include<cmath>
#include<set>
#include<map>
#include<cctype>
#include<list>
#define M 100099
#define INF 0x3f3f3f3f
using namespace std;
long long int dis;
int n,m;
int c[M];
int minn=INF;
int maxn=-INF;
int ans=0;
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int check(int x) {//为什么要用二分,因为具有单调性并且有界(骚~
int num=0,now=0;//num已经搬走的,now目前的
for(int i=1; i<=n+1; i++) {//要到终点那块
if(c[i]-now<x) {//如果比当前枚举的最小距离还小就搬走
num++;
} else now=c[i];
}
if(num>m) return 0;//超过题目要求的
}
void erfen(int x,int y) {
int l=0,r=dis;
while(l<=r) {
int mid=(l+r) >> 1;
if(check(mid)) {
l=mid+1;
ans=mid;
} else {
r=mid-1;
}
}
}
int main() {
/*freopen("stone.in","r",stdin);
freopen("stone.out","w",stdout);*/
dis=read();
n=read();
m=read();
int l=0,r=dis;
for(int i=1; i<=n; i++) cin>>c[i];
c[n+1]=dis;
while(l<=r) {
int mid=(l+r) >> 1;
if(check(mid)) {
l=mid+1;
ans=mid;
} else {
r=mid-1;
}
}
cout<<ans;
}
3.铺设道路
题目描述
春春是一名道路工程师,负责铺设一条长度为 n 的道路。
铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n 块首尾相连的区域,一开始,第 i 块区域下陷的深度为 \(d_i\) 。
春春每天可以选择一段连续区间[L,R],填充这段区间中的每块区域,让其下陷深度减少 1。在选择区间时,需要保证,区间内的每块区域在填充前下陷深度均不为 0 。
春春希望你能帮他设计一种方案,可以在最短的时间内将整段道路的下陷深度都变为 0 。
输入输出格式
输入格式:
输入文件包含两行,第一行包含一个整数 n,表示道路的长度。 第二行包含 n 个整数,相邻两数间用一个空格隔开,第 i 个整数为 \(d_i\)。
输出格式:
输出文件仅包含一个整数,即最少需要多少天才能完成任务。
输入输出样例
输入样例#1:
6
4 3 2 5 3 5
输出样例#1:
9
说明
【样例解释】
一种可行的最佳方案是,依次选择: [1,6]、[1,6]、[1,2]、[1,1]、[4,6]、[4,4]、[4,4]、[6,6]、[6,6]。
【数据规模与约定】
对于 30% 的数据,1 ≤ n ≤ 10 ;
对于 70% 的数据,1 ≤ n ≤ 1000;
对于 100% 的数据,1 ≤ n ≤ 100000 , 0 ≤ \(d_i\) ≤ 10000。
开始犯傻:
这道题我居然**似的没看出来是原题(指积木大赛)(CCF:我抄我自己)。主要的心里路程还是很善良的,主要的code也就是两三行Q。咳咳,正经一点,两种思路。
(1)贪心思路:若a[i]>a[i-1],计数器sum+=a[i]-a[i-1];
验证:假设现在有一个坑,但旁边又有一个坑。
你肯定会选择把两个同时减1;
那么小的坑肯定会被大的坑“带着”填掉。
大的坑也会减少a[i]-a[i-1]的深度,可以说是“免费的”;
所以这样贪心是对的;(来自dalao)
#include<bits/stdc++.h>
using namespace std;
int n,a[100005];
long long ans=0;
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=2;i<=n;i++) if(a[i]>a[i-1]) ans+=a[i]-a[i-1];
cout<<ans+a[1];
return 0;
}
(2)递推思路:
用f[i]表示前i个坑所铺设的最少天数
那么要做的只需比较一下当前的a[i](就是坑的深度)和a[i−1],分两种情况:
如果a[i]<=a[i-1],那么在填a[i−1]时就可以顺便把a[i]填上,这样显然更优,所以f[i]=f[i-1];
否则的话,那么在填a[i−1]时肯定要尽量把a[i]一块填上,a[i]剩余的就单独填。。
所以,f[i]=f[i−1]+(a[i]−a[i−1])。
初始化f[1]=a[1],向后推就行了。(依旧来自dalao)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<stack>
#include<queue>
#include<map>
#include<list>
#include<set>
#include<cctype>
#include<bitset>
#define N 100111
int n,opt[N],uxv[N];
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int main(){
//freopen("road.in","r",stdin); freopen("road.out","w",stdout);
n=read();
for(int i=1;i<=n;i++) uxv[i]=read();
opt[1]=uxv[1];
for(int i=2;i<=n;i++) uxv[i]<=uxv[i-1] ? opt[i]=opt[i-1] : opt[i]=opt[i-1]+(uxv[i]-uxv[i-1]);
printf("%d",opt[n]);
}
4.花匠
题目描述
花匠栋栋种了一排花,每株花都有自己的高度。花儿越长越大,也越来越挤。栋栋决定把这排中的一部分花移走,将剩下的留在原地,使得剩下的花能有空间长大,同时,栋栋希望剩下的花排列得比较别致。
具体而言,栋栋的花的高度可以看成一列整数\(h_1\),\(h_2\),...,\(h_n\)。设当一部分花被移走后,剩下的花的高度依次为\(g_1\),\(g_2\),...,\(g_m\),则栋栋希望下面两个条件中至少有一个满足:
条件 A:对于所有\(g_{2i}\)>\(g_{2i-1}\),\(g_{2i}\)>\(g_{2i+1}\)
条件 B:对于所有\(g_{2i}\)<\(g_{2i-1}\),\(g_{2i}\)<\(g_{2i+1}\)
注意上面两个条件在m=1时同时满足,当m>1时最多有一个能满足。
请问,栋栋最多能将多少株花留在原地。
输入输出格式
输入格式:
第一行包含一个整数n,表示开始时花的株数。
第二行包含n个整数,依次为\(h_1\),\(h_2\),...,\(h_n\),表示每株花的高度。
输出格式:
一个整数m,表示最多能留在原地的花的株数。
输入输出样例
输入样例#1:
5
5 3 2 1 2
输出样例#1:
3
说明
【输入输出样例说明】
有多种方法可以正好保留3株花,例如,留下第1、4、5株,高度分别为5、1、2,满足条件 B。
【数据范围】
对于 20%的数据,n ≤ 10;
对于 30%的数据,n ≤ 25;
对于 70%的数据,n ≤ 1000,0 ≤ \(h_i\)≤ 1000;
对于 100%的数据,1≤n≤100,000,0≤\(h_i\)≤1,000,000,所有的\(h_i\)随机生成,所有随机数服从某区间内的均匀分布。
开始犯傻:
考前做luogu上DP的题,然后翻题解的时候看到个双倍经验(眼前一亮),发现那道题的双倍经验就是这道,但是当时只是看了看题目,觉得真的是双倍经验,然后默默点了加入任务计划。(我:MMP??)
废话不多bb,画个图来解释???(充满善意的微笑)
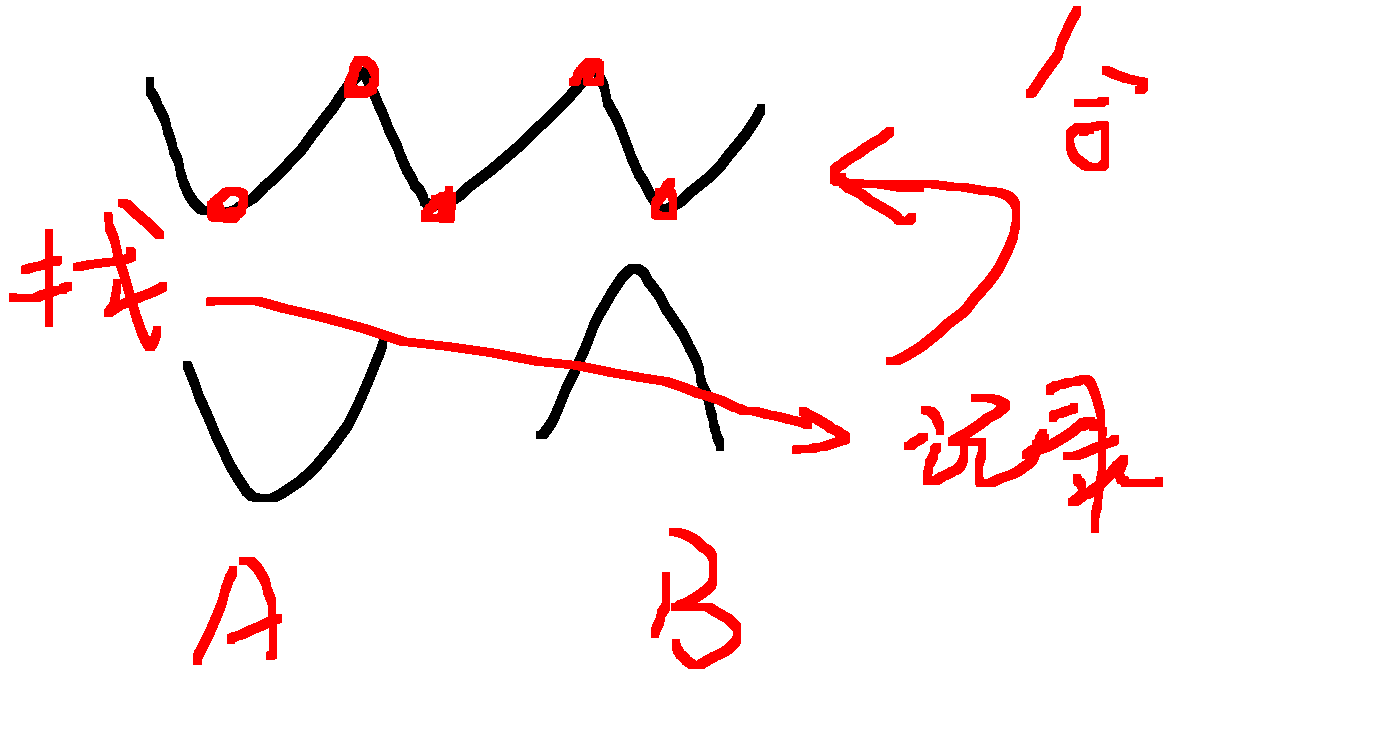
然后呐,就差不多是这个意思。要不再来解释下样例??(好的,又一次)
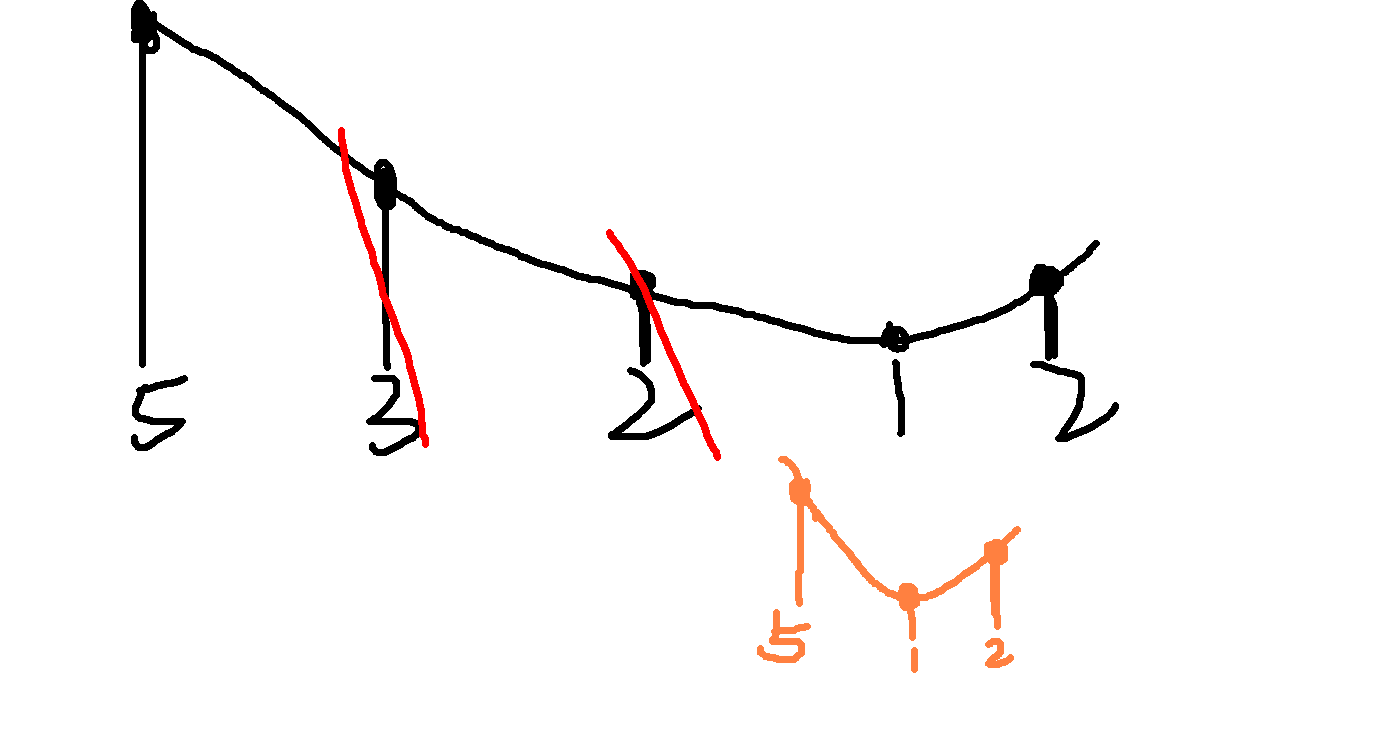
好的,差不多就是这个样子。
然后就非常的好理解了,让你找一个最长的大波浪序列,记录下波谷波峰就好啦。(这是dalao的想法,以下才是我的)用两个数组分别记录到i下降和到i上升。
这是dalao的代码:
#include<bits/stdc++.h>
using namespace std;
int n,h[1000005],ans=1;bool con;
int main()
{
cin>>n;for(int i=1;i<=n;i++) cin>>h[i];
if(h[2]>=h[1]) con=1;
for(int i=1;i<=n;i++)
{
if(con==0&&i==n) {ans++;break;}
if(con==1) if(h[i+1]<h[i]){ans++;con=0;continue;}
if(con==0) if(h[i+1]>h[i]) {ans++;con=1;continue;}
}
cout<<ans;
}
这是我的代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<queue>
#include<algorithm>
#include<cmath>
#include<set>
#include<map>
#include<cctype>
#include<list>
#define N 100055
using namespace std;
int h[N],f[N][3];
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int main() {
/*freopen("flower.in","r",stdin);
freopen("flower.out","w",stdin);*/
int n,ans=0;
n=read();
memset(f,0,sizeof(f));
for(int i=1; i<=n; i++) {
h[i]=read();
// f[i][0]=f[i][4]=1;
}
f[1][0]=f[1][5]=1;
for(int i=2; i<=n; i++) {
if(h[i]>h[i-1])
f[i][0]=f[i-1][6]+1;
else f[i][0]=f[i-1][0];
if(h[i]<h[i-1])
f[i][7]=f[i-1][0]+1;
else f[i][8]=f[i-1][9];
}
ans=max(f[n][0],f[n][10]);
cout<<ans<<endl;
}
5.货币系统
题目描述
在网友的国度中共有 nn 种不同面额的货币,第 i 种货币的面额为 a[i],你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 n、面额数组为 a[1..n] 的货币系统记作 (n,a)。
在一个完善的货币系统中,每一个非负整数的金额 x 都应该可以被表示出,即对每一个非负整数 x,都存在 n 个非负整数 t[i] 满足 a[i] \times t[i]a[i]×t[i] 的和为 xx。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 xx 不能被该货币系统表示出。例如在货币系统 n=3n=3, a=[2,5,9]a=[2,5,9] 中,金额 1,31,3 就无法被表示出来。
两个货币系统 (n,a)(n,a) 和 (m,b)(m,b) 是等价的,当且仅当对于任意非负整数 xx,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)(m,b),满足 (m,b)(m,b) 与原来的货币系统 (n,a)(n,a) 等价,且 mm 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 mm。
输入输出格式
输入格式:
输入文件的第一行包含一个整数 TT,表示数据的组数。
接下来按照如下格式分别给出 TT 组数据。 每组数据的第一行包含一个正整数 nn。接下来一行包含 nn 个由空格隔开的正整数 a[i]a[i]。
输出格式:
输出文件共有 TT 行,对于每组数据,输出一行一个正整数,表示所有与 (n,a)(n,a) 等价的货币系统 (m,b)(m,b) 中,最小的 mm。
输入输出样例
输入样例#1:
2
4
3 19 10 6
5
11 29 13 19 17
输出样例#1:
2
5
说明
在第一组数据中,货币系统(2,[3,10])和给出的货币系统(n,a)等价,并可以验证不存在 m < 2 的等价的货币系统,因此答案为 22。
在第二组数据中,可以验证不存在 m < n 的等价的货币系统,因此答案为 5。
【数据范围与约定】
![][11]
对于 100% 的数据,满足 1 ≤ T ≤ 20, n,a[i] ≥ 1。
开始犯傻:
考试时,题面我都没搞懂,我是来搞笑的嘛Q?改题时:逐渐开始佩服我自己,还是Orz一下我们的loceaner大佬吧。
附上dalao的思路:
先解释一下样例1中第一组数据的3,10,19,6等价于3,10的原因
6=3+3,19=3+3+3+10
即13,19都可以被凑出来
而第二组中的5个数都不能将其他的数凑出来(或被凑出来)
所以直接输出了5
所以就排序看看能不能凑出来就好啦
a[i]=0表示没有i这个数,a[i]=1表示可以凑出i这个数,a[i]=2表示本身就有i这个数
如果处理完成之后a[1~n]中还有等于2的(即本身就有这个数并且不能凑(只能他凑别人))
就让ans++,最后输出就好了
说实在的我看懂了,但是我不知道为啥我打不出来,惨
附上dalao的代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<deque>
#define INF 0x3f3f3f3f
using namespace std;
int a[25001];
int b[101];
int t,n,ans=0;
inline int read() {
char c=getchar();
int x=0,f=1;
while(c<'0'||c>'9') {if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-48,c=getchar();
return x*f;
}
int main() {
//freopen("money.in","r",stdin);
//freopen("money.out","w",stdout);
t=read();
while (t--) {
ans=0;
memset(a,0,sizeof(a));
scanf("%d",&n);
for (int i=1; i<=n; i++) {
b[i]=read();
a[b[i]]=2;//本身就有b[i]这个数;
}
sort(b+1,b+1+n);//从小到大排序
for (int i=1; i<=b[n]; i++) {
if(a[i]>0) {//如果可以凑出i
//那么也可以凑出i+b[j]
for(int j=1; j<=n; j++) {
if(i+b[j]<=b[n])//排序之后,b[n]一定是b数组中最大的数,在这里防止越界
a[i+b[j]]=1;
else break;//越界的话直接退出
}
}
}
for(int i=1; i<=b[n]; i++)
if(a[i]==2) ans++;//统计a[i]==2的个数输出
printf("%d\n",ans);
}
}
我太LJ了,所以代码还是看dalao的比较实在。
6.寻找道路
题目描述
在有向图 G 中,每条边的长度均为1,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
路径上的所有点的出边所指向的点都直接或间接与终点连通。
在满足条件1的情况下使路径最短。
注意:图 G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
输入输出格式
输入格式:
第一行有两个用一个空格隔开的整数 n 和 m,表示图有 n 个点和 m 条边。
接下来的 m 行每行 2 个整数 x,y之间用一个空格隔开,表示有一条边从点 x 指向点y。
最后一行有两个用一个空格隔开的整数 s, t表示起点为 s,终点为 t。
输出格式:
输出只有一行,包含一个整数,表示满足题目描述的最短路径的长度。如果这样的路径不存在,输出−1。
输入输出样例
输入样例#1:
3 2
1 2
2 1
1 3
输出样例#1:
-1
输入样例#2:
6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5
输出样例#2:
3
说明
解释1:
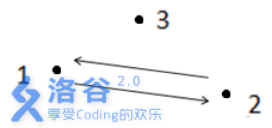
如上图所示,箭头表示有向道路,圆点表示城市。起点1与终点3不连通,所以满足题目描述的路径不存在,故输出−1 。
解释2:
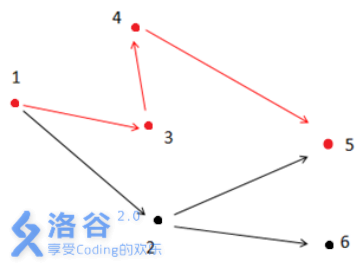
如上图所示,满足条件的路径为1->3->4->5。注意点2不能在答案路径中,因为点2连了一条边到点6,而点6 不与终点5 连通。
【数据范围】
对于30%的数据,0 < n ≤ 10,0 < m ≤ 20;
对于60%的数据,0 < n ≤ 100,0 < m ≤ 2000;
对于100%的数据,0 < n ≤ 10000 ,0 < m ≤ 200000,0 < x , y , s , t ≤ n,x,s ≠ t。
开始犯傻:
我不会这道题!!!
我不会这道!!!
我不会这!!!
我不会!!!
我不!!!
我!!!
!!!
!!
!
所以直接放代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iomanip>
#include<stack>
#include<queue>
#include<map>
#include<list>
#include<set>
#include<cctype>
#include<bitset>
#define N 20000
#define M 400000
#define Q 300000
#define INF 0x7fffffff
using namespace std;
struct edge {
int u,v,next;
//int num;
} a[M];
int head[N];
bool vis[N];
int num=0;
int n,m;
int s,t;
bool lala[N],mama[N];
int opt[N],uxv[N];
void add_edge(int x,int y) {
a[++num].u=x;
a[num].v=y;
a[num].next=head[x];
head[x]=num;
}
inline int read() {
int num=0,f=1;
char c=getchar();
for(; !isdigit(c); c=getchar()) if(c=='-') f=-1;
for(; isdigit(c); c=getchar()) num=num*10+c-'0';
return num*f;
}
int SPFA(int x,int y) {
int headd=-1,tail=0;
for(int i=1; i<=n; i++) opt[i]=INF;
opt[x]=0;
uxv[0]=x;
vis[x]=mama[x]=true;
while(headd!=tail) {
headd=(headd+1)%M;
int uu=uxv[headd];
int vv;
for(int i=head[uu]; i; i=a[i].next)
if(opt[uu]+1<opt[vv=a[i].v]) {
opt[vv]=opt[uu]+1;
if(!vis[vv]) {
tail=(tail+1)%M;
uxv[tail]=vv;
vis[vv]=true;
mama[vv]=true;
}
}
vis[uu]=false;
}
if(opt[y]==INF)
return -1;
return opt[y];
}
int main() {
/*freopen("road.in","r",stdin);
freopen("road.out","w",stdout);*/
n=read();
m=read();
for(int i=1; i<=m; i++) {
int x,y;
x=read();
y=read();
add_edge(y,x);
}
s=read();
t=read();
SPFA(t,n+1);
for(int i=1; i<=n; i++) lala[i]=mama[i];
for(int i=1; i<=m; i++)
if(mama[a[i].u]==false)
lala[a[i].v]=false;
memset(head,0,sizeof(head));
memset(vis,false,sizeof(vis));
num=0;
for(int i=1; i<=m; i++)
if(lala[a[i].u] && lala[a[i].v])
add_edge(a[i].v,a[i].u);
printf("%d\n",SPFA(s,t));
return 0;
}
综上所述:我就是个弟弟。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号