数据结构与算法知识树整理——算法篇——基本算法思想

算法知识树整理

基本算法思想

• 贪心算法

  • 何理解“贪心算法”？

    • 假设我们有一个可以容纳 100kg 物品的背包，可以装各种物品。我们有以下 5 种豆子，每种豆子的总量和总价值都各不相同。为了让背包中所装物品的总价值最大，我们如何选择在背包中装哪些豆子？每种豆子又该装多少呢？

      

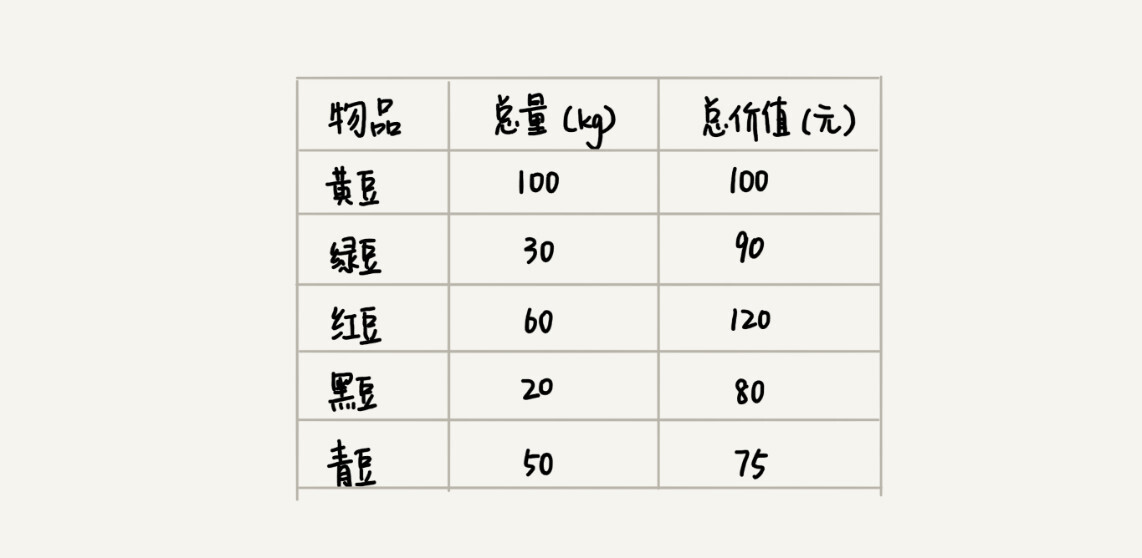
      实际上，这个问题很简单，我估计你一下子就能想出来，没错，我们只要先算一算每个物品的单价，按照单价由高到低依次来装就好了。单价从高到低排列，依次是：黑豆、绿豆、红豆、青豆、黄豆，所以，我们可以往背包里装 20kg 黑豆、30kg 绿豆、50kg 红豆。

      这个问题的解决思路显而易见，它本质上借助的就是贪心算法。结合这个例子，我总结一下贪心算法解决问题的步骤。

      1. 当我们看到这类问题的时候，首先要联想到贪心算法：针对一组数据，我们定义了限制值和期望值，希望从中选出几个数据，在满足限制值的情况下，期望值最大。类比到刚刚的例子，限制值就是重量不能超过 100kg，期望值就是物品的总价值。这组数据就是 5 种豆子。我们从中选出一部分，满足重量不超过 100kg，并且总价值最大。
      2. 我们尝试看下这个问题是否可以用贪心算法解决：每次选择当前情况下，在对限制值同等贡献量的情况下，对期望值贡献最大的数据。类比到刚刚的例子，我们每次都从剩下的豆子里面，选择单价最高的，也就是重量相同的情况下，对价值贡献最大的豆子。
      3. 我们举几个例子看下贪心算法产生的结果是否是最优的。大部分情况下，举几个例子验证一下就可以了。严格地证明贪心算法的正确性，是非常复杂的，需要涉及比较多的数学推理。而且，从实践的角度来说，大部分能用贪心算法解决的问题，贪心算法的正确性都是显而易见的，也不需要严格的数学推导证明。

      实际上，用贪心算法解决问题的思路，并不总能给出最优解。

      我来举一个例子。在一个有权图中，我们从顶点 S 开始，找一条到顶点 T 的最短路径（路径中边的权值和最小）。贪心算法的解决思路是，每次都选择一条跟当前顶点相连的权最小的边，直到找到顶点 T。按照这种思路，我们求出的最短路径是 S->A->E->T，路径长度是 1+4+4=9。

      

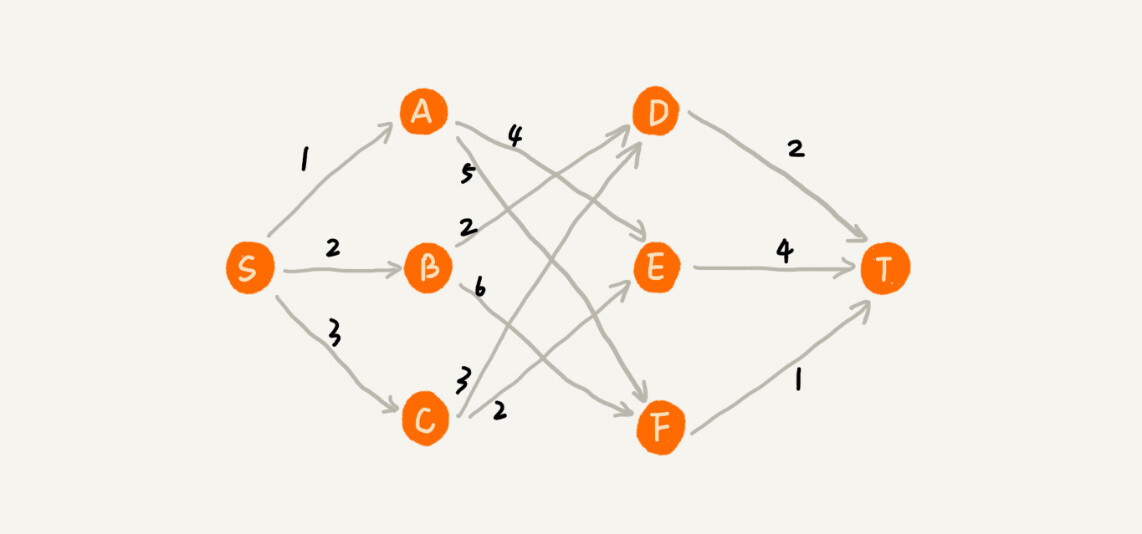
      但是，这种贪心的选择方式，最终求的路径并不是最短路径，因为路径 S->B->D->T 才是最短路径，因为这条路径的长度是 2+2+2=6。为什么贪心算法在这个问题上不工作了呢？

      在这个问题上，贪心算法不工作的主要原因是，前面的选择，会影响后面的选择。如果我们第一步从顶点 S 走到顶点 A，那接下来面对的顶点和边，跟第一步从顶点 S 走到顶点 B，是完全不同的。所以，即便我们第一步选择最优的走法（边最短），但有可能因为这一步选择，导致后面每一步的选择都很糟糕，最终也就无缘全局最优解了。

  • 贪心算法实战分析

    • 分糖果

      • 题目
        • 我们有 m 个糖果和 n 个孩子。我们现在要把糖果分给这些孩子吃，但是糖果少，孩子多（m<n），所以糖果只能分配给一部分孩子。每个糖果的大小不等，这 m 个糖果的大小分别是 s1，s2，s3，……，sm。除此之外，每个孩子对糖果大小的需求也是不一样的，只有糖果的大小大于等于孩子的对糖果大小的需求的时候，孩子才得到满足。假设这 n 个孩子对糖果大小的需求分别是 g1，g2，g3，……，gn。
        • 如何分配糖果，能尽可能满足最多数量的孩子？
      • 解题思路
        • 我们可以把这个问题抽象成，从 n 个孩子中，抽取一部分孩子分配糖果，让满足的孩子的个数（期望值）是最大的。这个问题的限制值就是糖果个数 m。
        • 我们现在来看看如何用贪心算法来解决。对于一个孩子来说，如果小的糖果可以满足，我们就没必要用更大的糖果，这样更大的就可以留给其他对糖果大小需求更大的孩子。另一方面，对糖果大小需求小的孩子更容易被满足，所以，我们可以从需求小的孩子开始分配糖果。因为满足一个需求大的孩子跟满足一个需求小的孩子，对我们期望值的贡献是一样的。
        • 我们每次从剩下的孩子中，找出对糖果大小需求最小的，然后发给他剩下的糖果中能满足他的最小的糖果，这样得到的分配方案，也就是满足的孩子个数最多的方案。

    • 钱币找零

      • 题目
        • 这个问题在我们的日常生活中更加普遍。假设我们有 1 元、2 元、5 元、10 元、20 元、50 元、100 元这些面额的纸币，它们的张数分别是 c1、c2、c5、c10、c20、c50、c100。我们现在要用这些钱来支付 K 元，最少要用多少张纸币呢？
      • 解题思路
        • 在生活中，我们肯定是先用面值最大的来支付，如果不够，就继续用更小一点面值的，以此类推，最后剩下的用 1 元来补齐。
        • 在贡献相同期望值（纸币数目）的情况下，我们希望多贡献点金额，这样就可以让纸币数更少，这就是一种贪心算法的解决思路。直觉告诉我们，这种处理方法就是最好的。实际上，要严谨地证明这种贪心算法的正确性，需要比较复杂的、有技巧的数学推导，我不建议你花太多时间在上面，不过如果感兴趣的话，可以自己去研究下。

    • 区间覆盖

      • 题目

        • 假设我们有 n 个区间，区间的起始端点和结束端点分别是[l1, r1]，[l2, r2]，[l3, r3]，……，[ln, rn]。我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交（端点相交的情况不算相交），最多能选出多少个区间呢？

          

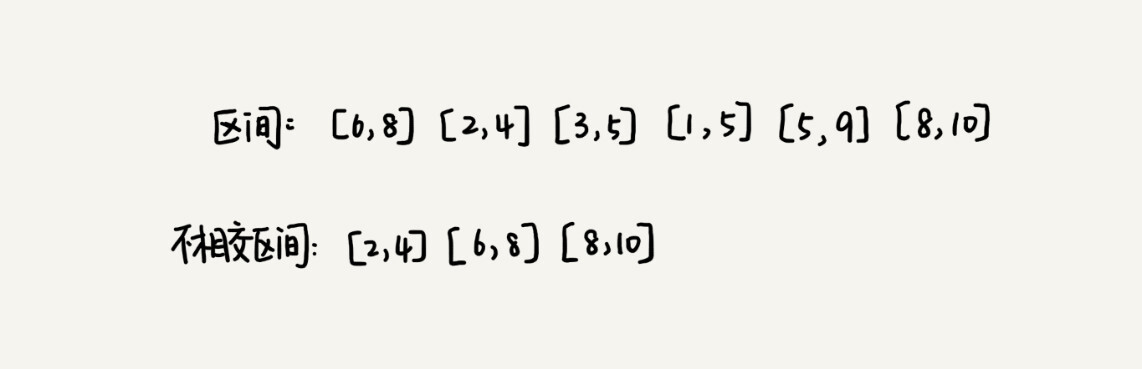
      • 解题思路

        • 这个问题的处理思路稍微不是那么好懂，不过，我建议你最好能弄懂，因为这个处理思想在很多贪心算法问题中都有用到，比如任务调度、教师排课等等问题。

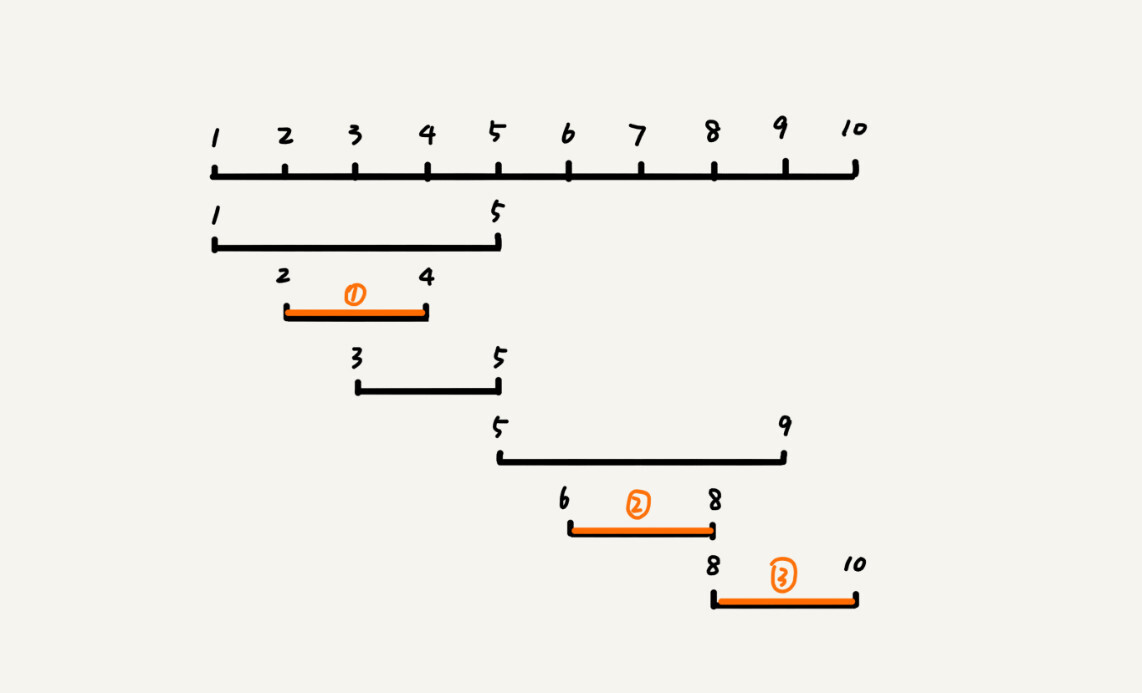
        • 这个问题的解决思路是这样的：我们假设这 n 个区间中最左端点是 lmin，最右端点是 rmax。这个问题就相当于，我们选择几个不相交的区间，从左到右将[lmin, rmax]覆盖上。我们按照起始端点从小到大的顺序对这 n 个区间排序。

        • 我们每次选择的时候，左端点跟前面的已经覆盖的区间不重合的，右端点又尽量小的，这样可以让剩下的未覆盖区间尽可能的大，就可以放置更多的区间。这实际上就是一种贪心的选择方法。

          

    • 霍夫曼编码

      • 题目

        • 假设我有一个包含 1000 个字符的文件，每个字符占 1 个 byte（1byte=8bits），存储这 1000 个字符就一共需要 8000bits，那有没有更加节省空间的存储方式呢？

      • 解题思路

        • 假设我们通过统计分析发现，这 1000 个字符中只包含 6 种不同字符，假设它们分别是 a、b、c、d、e、f。而 3 个二进制位（bit）就可以表示 8 个不同的字符，所以，为了尽量减少存储空间，每个字符我们用 3 个二进制位来表示。那存储这 1000 个字符只需要 3000bits 就可以了，比原来的存储方式节省了很多空间。a(000)、b(001)、c(010)、d(011)、e(100)、f(101)

        • 不过，还有没有更加节省空间的存储方式呢？

        • 霍夫曼编码就要登场了。霍夫曼编码是一种十分有效的编码方法，广泛用于数据压缩中，其压缩率通常在 20%～90% 之间。

        • 霍夫曼编码不仅会考察文本中有多少个不同字符，还会考察每个字符出现的频率，根据频率的不同，选择不同长度的编码。霍夫曼编码试图用这种不等长的编码方法，来进一步增加压缩的效率。如何给不同频率的字符选择不同长度的编码呢？根据贪心的思想，我们可以把出现频率比较多的字符，用稍微短一些的编码；出现频率比较少的字符，用稍微长一些的编码。

        • 为了避免解压缩过程中的歧义，霍夫曼编码要求各个字符的编码之间，不会出现某个编码是另一个编码前缀的情况。

        • 假设这 6 个字符出现的频率从高到低依次是 a、b、c、d、e、f。我们把它们编码下面这个样子，任何一个字符的编码都不是另一个的前缀，在解压缩的时候，我们每次会读取尽可能长的可解压的二进制串，所以在解压缩的时候也不会歧义。经过这种编码压缩之后，这 1000 个字符只需要 2100bits 就可以了。

          

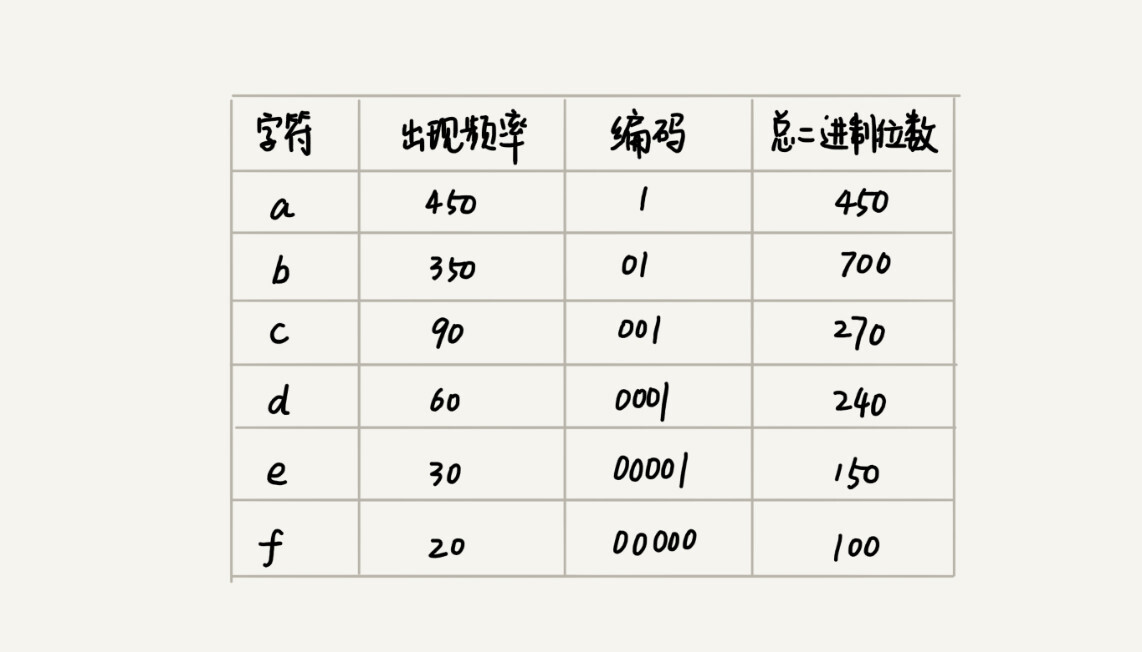
        • 尽管霍夫曼编码的思想并不难理解，但是如何根据字符出现频率的不同，给不同的字符进行不同长度的编码呢？这里的处理稍微有些技巧。

        • 我们把每个字符看作一个节点，并且附带着把频率放到优先级队列中。我们从队列中取出频率最小的两个节点 A、B，然后新建一个节点 C，把频率设置为两个节点的频率之和，并把这个新节点 C 作为节点 A、B 的父节点。最后再把 C 节点放入到优先级队列中。重复这个过程，直到队列中没有数据。

          

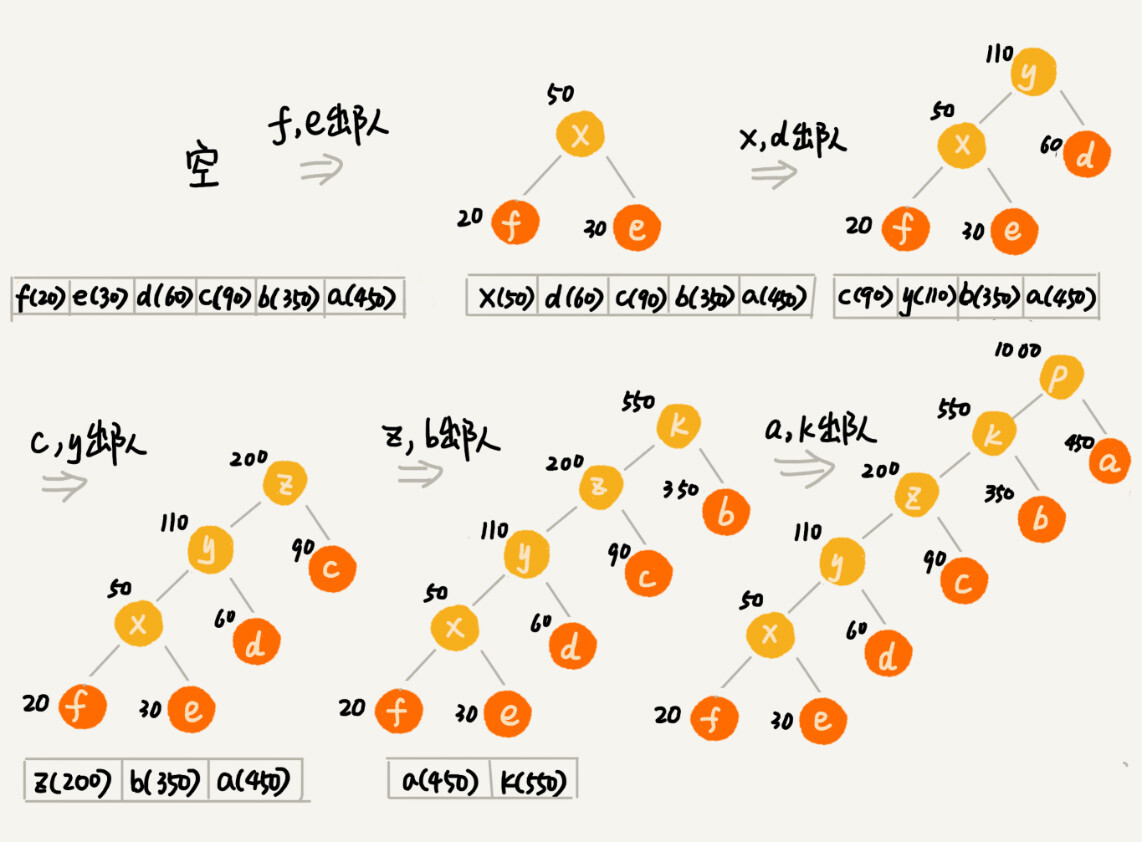
        • 现在，我们给每一条边加上画一个权值，指向左子节点的边我们统统标记为 0，指向右子节点的边，我们统统标记为 1，那从根节点到叶节点的路径就是叶节点对应字符的霍夫曼编码。

          

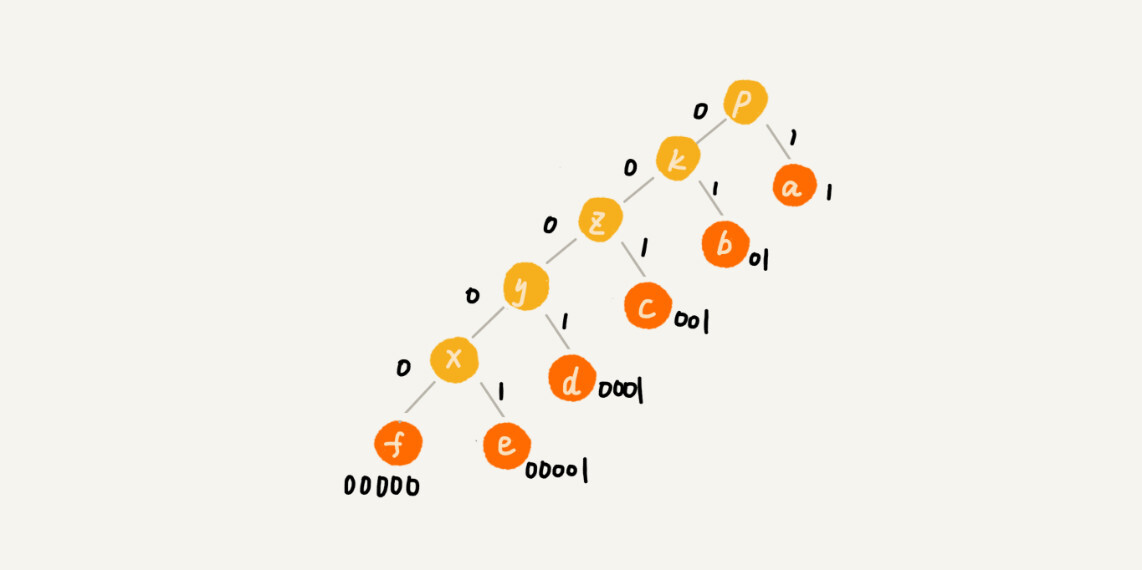
• 分治算法

  • 如何理解分治算法？

    • 分治算法（divide and conquer）的核心思想其实就是四个字，分而治之 ，也就是将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。
    • 这个定义看起来有点类似递归的定义。关于分治和递归的区别，我们在排序（下）的时候讲过，分治算法是一种处理问题的思想，递归是一种编程技巧。实际上，分治算法一般都比较适合用递归来实现。分治算法的递归实现中，每一层递归都会涉及这样三个操作
      • 分解：将原问题分解成一系列子问题；
      • 解决：递归地求解各个子问题，若子问题足够小，则直接求解；
      • 合并：将子问题的结果合并成原问题。
    • 分治算法能解决的问题，一般需要满足下面这几个条件：
      • 原问题与分解成的小问题具有相同的模式；
      • 原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别，等我们讲到动态规划的时候，会详细对比这两种算法；
      • 具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
      • 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

  • 分治算法应用举例分析

    • 题目一

      • 假设我们有 n 个数据，我们期望数据从小到大排列，那完全有序的数据的有序度就是 n(n-1)/2，逆序度等于 0；相反，倒序排列的数据的有序度就是 0，逆序度是 n(n-1)/2。除了这两种极端情况外，我们通过计算有序对或者逆序对的个数，来表示数据的有序度或逆序度。

        

        如何编程求出一组数据的有序对个数或者逆序对个数呢？

      • 解法思路

        • 我们套用分治的思想来求数组 A 的逆序对个数。我们可以将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。

        • 我们前面讲过，使用分治算法其中一个要求是，子问题合并的代价不能太大，否则就起不了降低时间复杂度的效果了。那回到这个问题，如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢？

        • 归并排序中有一个非常关键的操作，就是将两个有序的小数组，合并成一个有序的数组。实际上，在这个合并的过程中，我们就可以计算这两个小数组的逆序对个数了。每次合并操作，我们都计算逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数了。

          

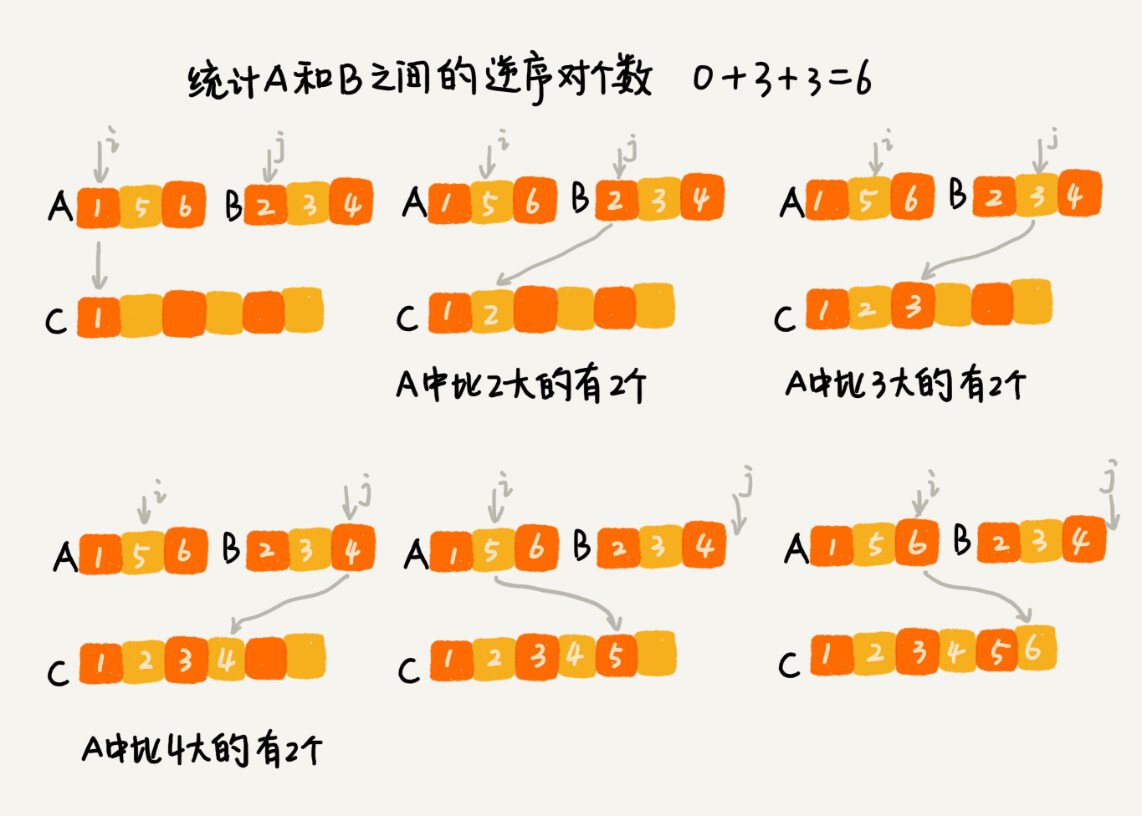
          private int num = 0; // 全局变量或者成员变量
          public int count(int[] a, int n) {
            num = 0;
            mergeSortCounting(a, 0, n-1);
            return num;
          }
          
          private void mergeSortCounting(int[] a, int p, int r) {
            if (p >= r) return;
            int q = (p+r)/2;
            mergeSortCounting(a, p, q);
            mergeSortCounting(a, q+1, r);
            merge(a, p, q, r);
          }
          
          private void merge(int[] a, int p, int q, int r) {
            int i = p, j = q+1, k = 0;
            int[] tmp = new int[r-p+1];
            while (i<=q && j<=r) {
              if (a[i] <= a[j]) {
                tmp[k++] = a[i++];
              } else {
                num += (q-i+1); // 统计p-q之间，比a[j]大的元素个数
                tmp[k++] = a[j++];
              }
            }
            while (i <= q) { // 处理剩下的
              tmp[k++] = a[i++];
            }
            while (j <= r) { // 处理剩下的
              tmp[k++] = a[j++];
            }
            for (i = 0; i <= r-p; ++i) { // 从tmp拷贝回a
              a[p+i] = tmp[i];
            }
          }
          

    • 题目二

      • 二维平面上有 n 个点，如何快速计算出两个距离最近的点对？
      • 解题思路
        • 取中间点即可，使分出的两半尽量大小相同，然后分别计算左右两半最短距离，求出min值d，然后关键是计算两半之间交界处的最短距离；
        • 根据min值d在中间的划分线两边画两条带子，宽度左右各为d，只有在这个交界区域的点对才可能有更短距离；
        • 这个区域的点对也不必全部遍历，比如左侧某点p，右侧的q需在一个高2d*宽d的矩形内才可能使两者距离小于d，而这个矩形内至多只可能放入6个点（极端情况即为四个角加上两长边中点）
        • 最后递归求解，时间复杂度为O(nlogn)

    • 题目三

      • 有两个 nn 的矩阵 A，B，如何快速求解两个矩阵的乘积 C=AB？
      • 解题思路
        • 斯特拉森提出了2*2分块矩阵的计算公式 从原来的8次乘法 缩减到了7次，当n规模很大的时候 缩减效果就很明显 （7/8）^(logn)

• 回溯算法

  • 如何理解“回溯算法”？

    • 笼统地讲，回溯算法很多时候都应用在“搜索”这类问题上。不过这里说的搜索，并不是狭义的指我们前面讲过的图的搜索算法，而是在一组可能的解中，搜索满足期望的解。
    • 回溯的处理思想，有点类似枚举搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

  • 回溯算法的经典应用

    • 八皇后问题。

      • 题目

        • 我们有一个 8x8 的棋盘，希望往里放 8 个棋子（皇后），每个棋子所在的行、列、对角线都不能有另一个棋子。你可以看我画的图，第一幅图是满足条件的一种方法，第二幅图是不满足条件的。八皇后问题就是期望找到所有满足这种要求的放棋子方式。

          

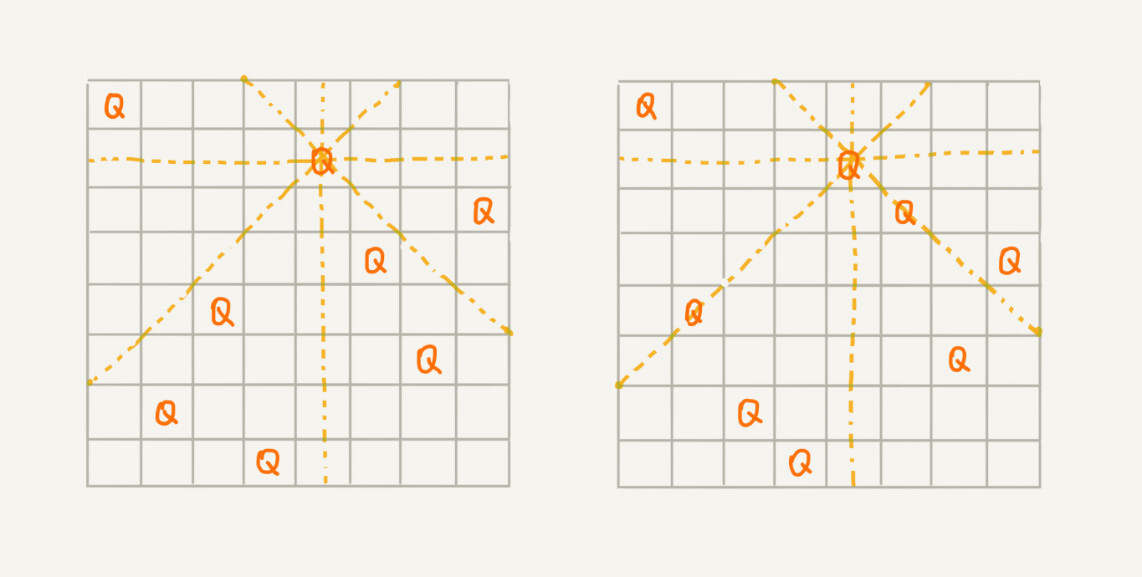
        • 解题思路

          • 我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中，我们不停地检查当前放法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种放法，继续尝试。

          • 回溯算法非常适合用递归代码实现，所以，我把八皇后的算法翻译成代码。我在代码里添加了详细的注释，你可以对比着看下。如果你之前没有接触过八皇后问题，建议你自己用熟悉的编程语言实现一遍，这对你理解回溯思想非常有帮助

            int[] result = new int[8];//全局或成员变量,下标表示行,值表示queen存储在哪一列
            public void cal8queens(int row) { // 调用方式：cal8queens(0);
              if (row == 8) { // 8个棋子都放置好了，打印结果
                printQueens(result);
                return; // 8行棋子都放好了，已经没法再往下递归了，所以就return
              }
              for (int column = 0; column < 8; ++column) { // 每一行都有8中放法
                if (isOk(row, column)) { // 有些放法不满足要求
                  result[row] = column; // 第row行的棋子放到了column列
                  cal8queens(row+1); // 考察下一行
                }
              }
            }
            
            private boolean isOk(int row, int column) {//判断row行column列放置是否合适
              int leftup = column - 1, rightup = column + 1;
              for (int i = row-1; i >= 0; --i) { // 逐行往上考察每一行
                if (result[i] == column) return false; // 第i行的column列有棋子吗？
                if (leftup >= 0) { // 考察左上对角线：第i行leftup列有棋子吗？
                  if (result[i] == leftup) return false;
                }
                if (rightup < 8) { // 考察右上对角线：第i行rightup列有棋子吗？
                  if (result[i] == rightup) return false;
                }
                --leftup; ++rightup;
              }
              return true;
            }
            
            private void printQueens(int[] result) { // 打印出一个二维矩阵
              for (int row = 0; row < 8; ++row) {
                for (int column = 0; column < 8; ++column) {
                  if (result[row] == column) System.out.print("Q ");
                  else System.out.print("* ");
                }
                System.out.println();
              }
              System.out.println();
            }
            

      • 0-1 背包

        • 0-1 背包是非常经典的算法问题，很多场景都可以抽象成这个问题模型。这个问题的经典解法是动态规划，不过还有一种简单但没有那么高效的解法，那就是回溯算法。动态规划的解法后面谈，我们先来看下，如何用回溯法解决这个问题。

        • 题目

          • 0-1 背包问题有很多变体，我这里介绍一种比较基础的。我们有一个背包，背包总的承载重量是 Wkg。现在我们有 n 个物品，每个物品的重量不等，并且不可分割。我们现在期望选择几件物品，装载到背包中。在不超过背包所能装载重量的前提下，如何让背包中物品的总重量最大？

        • 解法

          • 实际上，背包问题我们在贪心算法那里已经讲过一个了，不过那里讲的物品是可以分割的，我可以装某个物品的一部分到背包里面。今天讲的这个背包问题，物品是不可分割的，要么装要么不装，所以叫 0-1 背包问题。显然，这个问题已经无法通过贪心算法来解决了。我们现在来看看，用回溯算法如何来解决。

          • 我们可以把物品依次排列，整个问题就分解为了 n 个阶段，每个阶段对应一个物品怎么选择。先对第一个物品进行处理，选择装进去或者不装进去，然后再递归地处理剩下的物品。

            public int maxW = Integer.MIN_VALUE; //存储背包中物品总重量的最大值
            // cw表示当前已经装进去的物品的重量和；i表示考察到哪个物品了；
            // w背包重量；items表示每个物品的重量；n表示物品个数
            // 假设背包可承受重量100，物品个数10，物品重量存储在数组a中，那可以这样调用函数：
            // f(0, 0, a, 10, 100)
            public void f(int i, int cw, int[] items, int n, int w) {
              if (cw == w || i == n) { // cw==w表示装满了;i==n表示已经考察完所有的物品
                if (cw > maxW) maxW = cw;
                return;
              }
              f(i+1, cw, items, n, w);
              if (cw + items[i] <= w) {// 已经超过可以背包承受的重量的时候，就不要再装了
                f(i+1,cw + items[i], items, n, w);
              }
            }
            

            这里还稍微用到了一点搜索剪枝的技巧，就是当发现已经选择的物品的重量超过 Wkg 之后，我们就停止继续探测剩下的物品。

      • 正则表达式

        • 题目

          • 正则表达式中，最重要的就是通配符，通配符结合在一起，可以表达非常丰富的语义。为了方便讲解，我假设正则表达式中只包含“”和“?”这两种通配符，并且对这两个通配符的语义稍微做些改变，其中，“”匹配任意多个（大于等于 0 个）任意字符，“?”匹配零个或者一个任意字符。基于以上背景假设，我们看下，如何用回溯算法，判断一个给定的文本，能否跟给定的正则表达式匹配？

        • 解题思路

          • 我们依次考察正则表达式中的每个字符，当是非通配符时，我们就直接跟文本的字符进行匹配，如果相同，则继续往下处理；如果不同，则回溯。

          • 如果遇到特殊字符的时候，我们就有多种处理方式了，也就是所谓的岔路口，比如“*”有多种匹配方案，可以匹配任意个文本串中的字符，我们就先随意的选择一种匹配方案，然后继续考察剩下的字符。如果中途发现无法继续匹配下去了，我们就回到这个岔路口，重新选择一种匹配方案，然后再继续匹配剩下的字符。

            public class Pattern {
              private boolean matched = false;
              private char[] pattern; // 正则表达式
              private int plen; // 正则表达式长度
            
              public Pattern(char[] pattern, int plen) {
                this.pattern = pattern;
                this.plen = plen;
              }
            
              public boolean match(char[] text, int tlen) { // 文本串及长度
                matched = false;
                rmatch(0, 0, text, tlen);
                return matched;
              }
            
              private void rmatch(int ti, int pj, char[] text, int tlen) {
                if (matched) return; // 如果已经匹配了，就不要继续递归了
                if (pj == plen) { // 正则表达式到结尾了
                  if (ti == tlen) matched = true; // 文本串也到结尾了
                  return;
                }
                if (pattern[pj] == '*') { // *匹配任意个字符
                  for (int k = 0; k <= tlen-ti; ++k) {
                    rmatch(ti+k, pj+1, text, tlen);
                  }
                } else if (pattern[pj] == '?') { // ?匹配0个或者1个字符
                  rmatch(ti, pj+1, text, tlen);
                  rmatch(ti+1, pj+1, text, tlen);
                } else if (ti < tlen && pattern[pj] == text[ti]) { // 纯字符匹配才行
                  rmatch(ti+1, pj+1, text, tlen);
                }
              }
            }
            

• 动态规划

  • 动态规划比较适合用来求解最优问题，比如求最大值、最小值等等。它可以非常显著地降低时间复杂度，提高代码的执行效率。

  • 入门举例

    • 0-1 背包问题

      • 题目

        • 对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制的前提下，背包中物品总重量的最大值是多少呢？

      • 解题思路

        • 关于这个问题，我们上一节讲了回溯的解决方法，也就是穷举搜索所有可能的装法，然后找出满足条件的最大值。

          private int MaxW = Int32.MinValue;
          private int[] weight = {2, 2, 4, 6, 3}; // 物品重量
          private int n = 5; // 物品个数
          private int w = 9; // 背包承受的最大重量
          
          //i 表示将要决策第几个物品是否装入背包，cw 表示当前背包中物品的总重量。
          public void f(int i, int cw)
          {
              if (i >= n || cw == 9)
              {
                  if (cw > MaxW)
                      MaxW = cw;
                  return;
              }
              //对于每个物品我都能选择拿或者不拿
              f(i + 1, cw);//不拿
              if (cw + weight[i] <= w )
              {
                  f(i + 1, cw + weight[i]); //拿
              }
          }
          

        • 不过，回溯算法的复杂度比较高，是指数级别的。那有没有什么规律，可以有效降低时间复杂度呢？

        • 规律是不是不好找？那我们就举个例子、画个图看看。我们假设背包的最大承载重量是 9。我们有 5 个不同的物品，每个物品的重量分别是 2，2，4，6，3。如果我们把这个例子的回溯求解过程，用递归树画出来，就是下面这个样子：

          

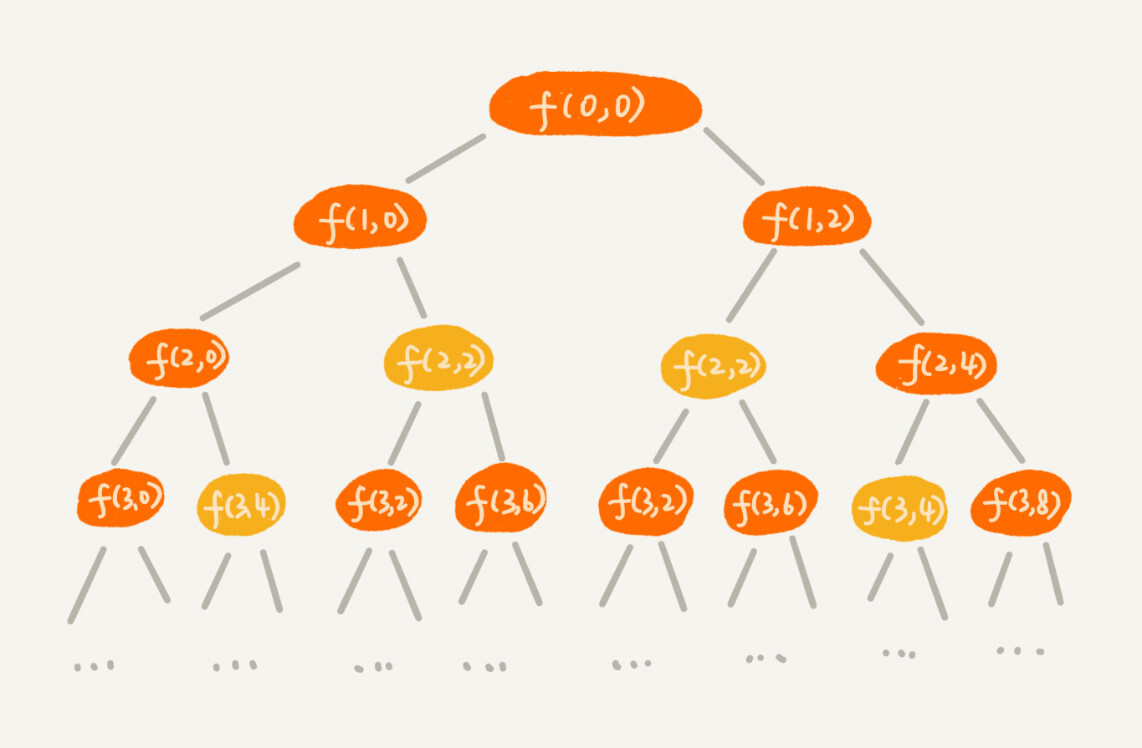
        • 递归树中的每个节点表示一种状态，我们用（i, cw）来表示。其中，i 表示将要决策第几个物品是否装入背包，cw 表示当前背包中物品的总重量。比如，（2，2）表示我们将要决策第 2 个物品是否装入背包，在决策前，背包中物品的总重量是 2。

        • 从递归树中，你应该能会发现，有些子问题的求解是重复的，比如图中 f(2, 2) 和 f(3,4) 都被重复计算了两次。我们可以借助递归那一节讲的“备忘录”的解决方式，记录已经计算好的 f(i, cw)，当再次计算到重复的 f(i, cw) 的时候，可以直接从备忘录中取出来用，就不用再递归计算了，这样就可以避免冗余计算。

          private int MaxW = Int32.MinValue;
          private int[] weight = {2, 2, 4, 6, 3}; // 物品重量
          private int n = 5; // 物品个数
          private int w = 9; // 背包承受的最大重量
          private bool[,] backups = new bool[5, 10]; // 备忘录，默认值false
          
          //i 表示将要决策第几个物品是否装入背包，cw 表示当前背包中物品的总重量。
          public void f(int i, int cw)
          {
              if (i >= n || cw + weight[i] > w || cw < 0)
              {
                  return;
              }
          
              if (backups[i, cw]) //往下的分支已经计算过了就不往下走了
                  return;
              else
                  backups[i, cw] = true;
          
              if (cw + weight[i] > MaxW)
                  MaxW = cw + weight[i];
              //对于每个物品我都能选择拿或者不拿
              f(i + 1, cw);//不拿
              f(i + 1, cw + weight[i]); //拿
          }
          

        • 这种解决方法非常好。实际上，它已经跟动态规划的执行效率基本上没有差别。但是，多一种方法就多一种解决思路，我们现在来看看动态规划是怎么做的。

          • 我们把整个求解过程分为 n 个阶段，每个阶段会决策一个物品是否放到背包中。每个物品决策（放入或者不放入背包）完之后，背包中的物品的重量会有多种情况，也就是说，会达到多种不同的状态，对应到递归树中，就是有很多不同的节点。

          • 我们把每一层重复的状态（节点）合并，只记录不同的状态，然后基于上一层的状态集合，来推导下一层的状态集合。我们可以通过合并每一层重复的状态，这样就保证每一层不同状态的个数都不会超过 w 个（w 表示背包的承载重量），也就是例子中的 9。于是，我们就成功避免了每层状态个数的指数级增长。

          • 我们用一个二维数组 states[n][w+1]，来记录每层可以达到的不同状态。

          • 第 0 个（下标从 0 开始编号）物品的重量是 2，要么装入背包，要么不装入背包，决策完之后，会对应背包的两种状态，背包中物品的总重量是 0 或者 2。我们用 states[0][0]=true 和 states[0][2]=true 来表示这两种状态。

          • 第 1 个物品的重量也是 2，基于之前的背包状态，在这个物品决策完之后，不同的状态有 3 个，背包中物品总重量分别是 0(0+0)，2(0+2 or 2+0)，4(2+2)。我们用 states[1][0]=true，states[1][2]=true，states[1][4]=true 来表示这三种状态

          • 以此类推，直到考察完所有的物品后，整个 states 状态数组就都计算好了。我把整个计算的过程画了出来，你可以看看。图中 0 表示 false，1 表示 true。我们只需要在最后一层，找一个值为 true 的最接近 w（这里是 9）的值，就是背包中物品总重量的最大值。

            

            

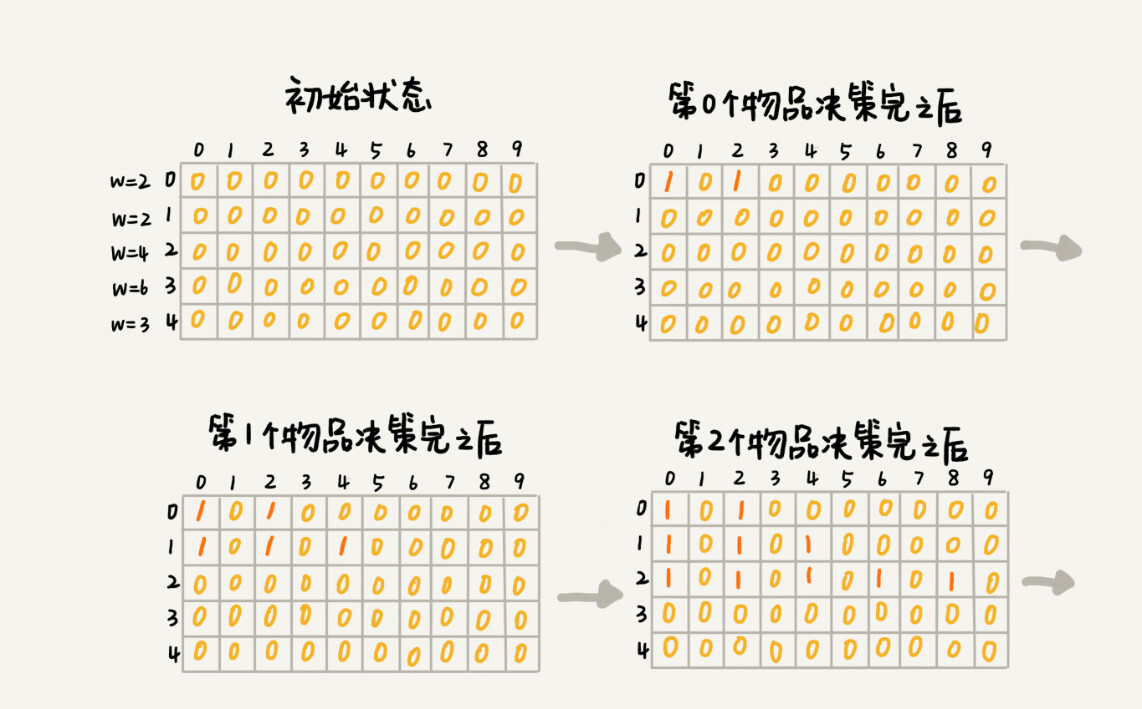
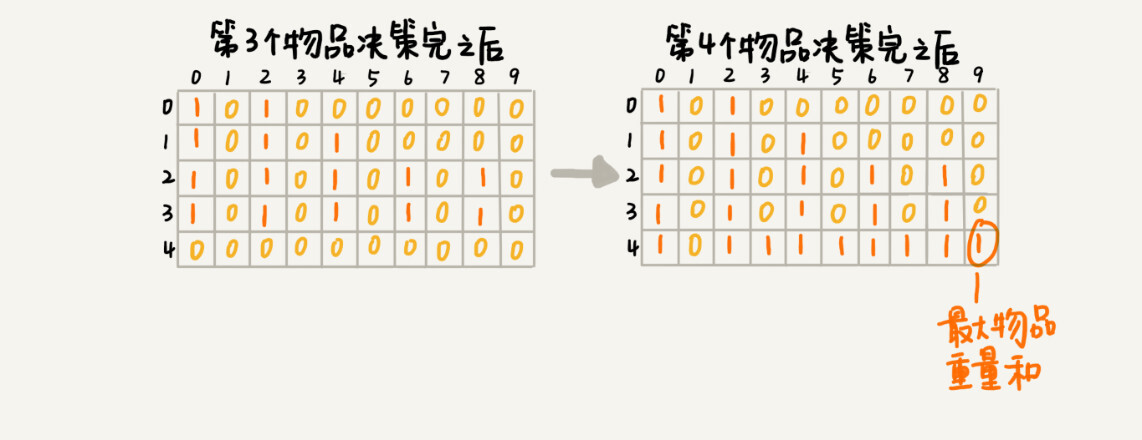
            //weight:物品重量，n:物品个数，w:背包可承载重量
            public int knapsack(int[] weight, int n, int w)
            {
                bool[,] states = new bool[n, w + 1];
                //第一行特殊处理
                states[0, 0] = true;
                if (weight[0] <= w) {
                    states[0, weight[0]] = true;
                }
                //从第二行开始以上一行的状态为准
                for (int i = 1; i < n; i++)
                {
                    for (int j = 0; j < w; j++)
                    {
                        if (states[i - 1, j])
                        {
                            states[i, j] = true;//状态转移，不把物品放入背包=前一个状态不变转移到下一个状态
                            if (j + weight[i] <= w)
                                states[i, j + weight[i]] = true;//把物品放入背包
                        }
            
                    }
                }
                for (int i = w; i >= 0; i--) // 输出结果
                {
                    if (states[n - 1, i])
                        return i;
                }
                return 0;
            }
            

          • 实际上，这就是一种用动态规划解决问题的思路。我们把问题分解为多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。这也是动态规划这个名字的由来，你可以自己体会一下，是不是还挺形象的？

          • 前面我们讲到，用回溯算法解决这个问题的时间复杂度 O(2^n)，是指数级的。那动态规划解决方案的时间复杂度是多少呢？我来分析一下。

          • 这个代码的时间复杂度非常好分析，耗时最多的部分就是代码中的两层 for 循环，所以时间复杂度是 O(n*w)。n 表示物品个数，w 表示背包可以承载的总重量。

          • 从理论上讲，指数级的时间复杂度肯定要比 O(n*w) 高很多，但是为了让你有更加深刻的感受，我来举一个例子给你比较一下

            • 我们假设有 10000 个物品，重量分布在 1 到 15000 之间，背包可以承载的总重量是 30000。如果我们用回溯算法解决，用具体的数值表示出时间复杂度，就是 2^10000，这是一个相当大的一个数字。如果我们用动态规划解决，用具体的数值表示出时间复杂度，就是 10000*30000。虽然看起来也很大，但是和 2^10000 比起来，要小太多了。

          • 尽管动态规划的执行效率比较高，但是就刚刚的代码实现来说，我们需要额外申请一个 n 乘以 w+1 的二维数组，对空间的消耗比较多。所以，有时候，我们会说，动态规划是一种空间换时间的解决思路。你可能要问了，有什么办法可以降低空间消耗吗？

          • 实际上，我们只需要一个大小为 w+1 的一维数组就可以解决这个问题。动态规划状态转移的过程，都可以基于这个一维数组来操作。具体的代码实现我贴在这里，你可以仔细看下。

             //weight:物品重量，n:物品个数，w:背包可承载重量
            public int knapsack(int[] weight, int n, int w)
            {
                bool[] states = new bool[w + 1];
                //第一行特殊处理
                states[0] = true;
                if (weight[0] <= w) {
                    states[weight[0]] = true;
                }
                //从第二行开始以上一行的状态为准
                for (int i = 1; i < n; i++)
                {
                    for (int j = 0; j < w; j++)
                    {
                        if (states[j] && j + weight[i] <= w)//核心优化就是如果不放就是把第一行状态转移到下一行，等于吧上次的数据拿来继续用就行
                        {
                            states[j + weight[i]] = true;//把物品放入背包
                        }
            
                    }
                }
            
                for (int i = w; i >= 0; i--) // 输出结果
                {
                    if (states[i])
                        return i;
                }
            
                return 0;
            }
            

    • 0-1 背包问题升级版

      • 题目

        • 我们刚刚讲的背包问题，只涉及背包重量和物品重量。我们现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品，我们选择将某些物品装入背包，在满足背包最大重量限制的前提下，背包中可装入物品的总价值最大是多少呢？

      • 解题思路

        • 老样子先写回溯版

          public void f(int i, int cw,int v)
          {
              if (i >= n || cw == w)
              {
                  if (v > MaxValue)
                      MaxValue = v;//都是遍历所有情况，唯一区别就是这里变成了计算最大价值
                  return;
              }
          
              //对于每个物品我都能选择拿或者不拿
              f(i + 1, cw, v);//不拿
              if (cw + weight[i] <= w )
              {
                  f(i + 1, cw + weight[i], v + value[i]); //拿
              }
          }
          

        • 画递归树

          在递归树中，每个节点表示一个状态。现在我们需要 3 个变量（i, cw, cv）来表示一个状态。其中，i 表示即将要决策第 i 个物品是否装入背包，cw 表示当前背包中物品的总重量，cv 表示当前背包中物品的总价值。

          

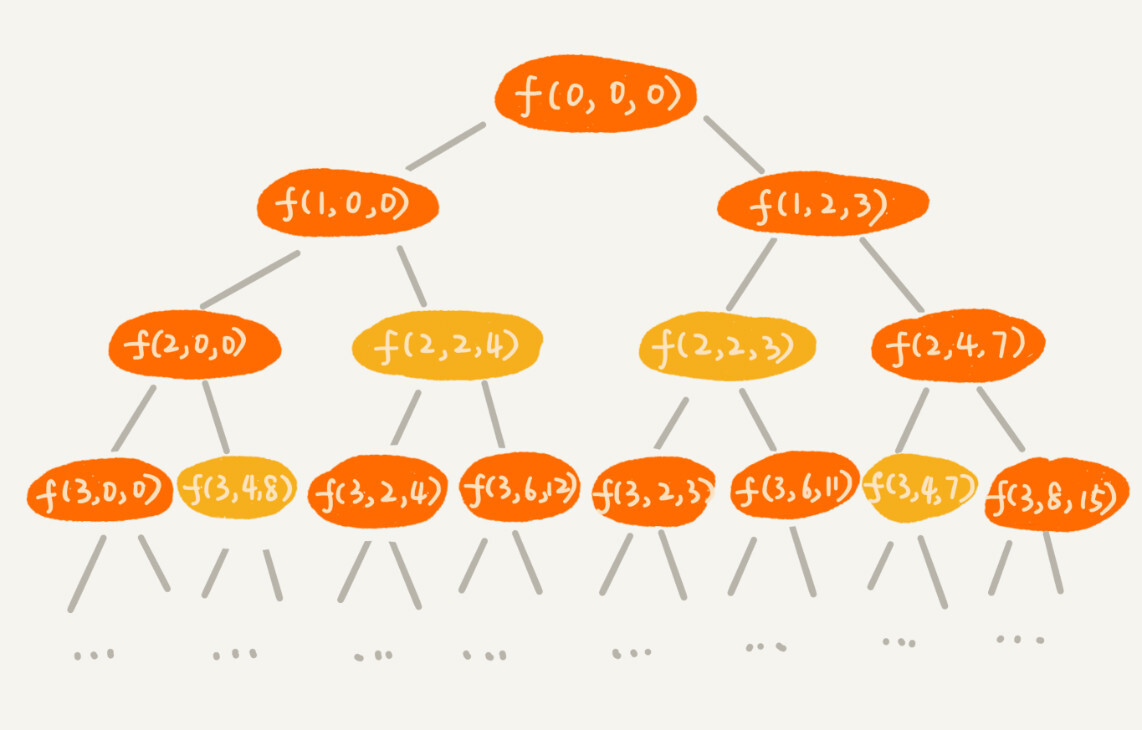
          我们发现，在递归树中，有几个节点的 i 和 cw 是完全相同的，比如 f(2,2,4) 和 f(2,2,3)。在背包中物品总重量一样的情况下，f(2,2,4) 这种状态对应的物品总价值更大，我们可以舍弃 f(2,2,3) 这种状态，只需要沿着 f(2,2,4) 这条决策路线继续往下决策就可以。

          也就是说，对于 (i, cw) 相同的不同状态，那我们只需要保留 cv 值最大的那个，继续递归处理，其他状态不予考虑。

        • 思考能不能用备忘录来做，如果可以则只需要魔改回溯就能提高到和动态规划一样的效率

          这里只是（i,cw）方式不能进行备忘方式了，因为V会变，但是（i,cw,cv）作为key仍然可以减少重复计算，只不过没动态规划的（i,cw）方式减少得多。所以考虑动态规划如何实现

        • 我们还是把整个求解过程分为 n 个阶段，每个阶段会决策一个物品是否放到背包中。每个阶段决策完之后，背包中的物品的总重量以及总价值，会有多种情况，也就是会达到多种不同的状态。

        • 我们用一个二维数组 states[n][w+1]，来记录每层可以达到的不同状态。不过这里数组存储的值不再是 boolean 类型的了，而是当前状态对应的最大总价值。我们把每一层中 (i, cw) 重复的状态（节点）合并，只记录 cv 值最大的那个状态，然后基于这些状态来推导下一层的状态。

          public int knapsack(int[] weight, int[] value, int n, int w)
          {
              int[,] states = new int[n, w + 1];//记录最大价值
              //第一行特殊处理
              states[0, 0] = 1;//为了省下遍历一次数组初始化值的操作，这里统一+1，之后不需要加1了，因为都是基于这个值运算，返回价值的时候统一-1
              if (weight[0] <= w)
              {
                  states[0, weight[0]] = value[0] + 1;
              }
              //从第二行开始以上一行的状态为准
              for (int i = 1; i < n; i++)
              {
                  for (int j = 0; j < w; j++)
                  {
                      if (states[i - 1, j] > 0)
                      {
                          states[i, j] = Math.Max(states[i - 1, j], states[i, j]);
                          int newW = j + weight[i];
                          if (newW <= w)
                          {
                              states[i, newW] = Math.Max(states[i, newW], states[i - 1, j] + value[i]);
                          }
                      }
          
                  }
              }
          
              int max = 0;
              for (int i = w; i >= 0; i--) // 输出结果
              {
                  if (states[n - 1, i] > max)
                      max = states[n - 1, i] - 1;
              }
          
              return max;
          }
          

          时间复杂度是 O(nw)，空间复杂度也是 O(nw)。

    • 双十一购物

      • 题目

        • 淘宝的“双十一”购物节有各种促销活动，比如“满 200 元减 50 元”。假设你女朋友的购物车中有 n 个（n>100）想买的商品，她希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（200 元）

      • 思路

        • 实际上，它跟第一个例子中讲的 0-1 背包问题很像，只不过是把“重量”换成了“价格”而已。购物车中有 n 个商品。我们针对每个商品都决策是否购买。每次决策之后，对应不同的状态集合。我们还是用一个二维数组 states[n][x]，来记录每次决策之后所有可达的状态。不过，这里的 x 值是多少呢？

        • 0-1 背包问题中，我们找的是小于等于 w 的最大值，x 就是背包的最大承载重量 w+1。对于这个问题来说，我们要找的是大于等于 200（满减条件）的值中最小的，所以就不能设置为 200 加 1 了。就这个实际的问题而言，如果要购买的物品的总价格超过 200 太多，比如 1000，那这个羊毛“薅”得就没有太大意义了。所以，我们可以限定 x 值为 1001。

        • 不过，这个问题不仅要求大于等于 200 的总价格中的最小的，我们还要找出这个最小总价格对应都要购买哪些商品。实际上，我们可以利用 states 数组，倒推出这个被选择的商品序列。我先把代码写出来，待会再照着代码给你解释

          // items商品价格，n商品个数, w表示满减条件，比如200
          public static void double11advance(int[] items, int n, int w) {
            boolean[][] states = new boolean[n][3*w+1];//超过3倍就没有薅羊毛的价值了
            states[0][0] = true;  // 第一行的数据要特殊处理
            if (items[0] <= 3*w) {
              states[0][items[0]] = true;
            }
            for (int i = 1; i < n; ++i) { // 动态规划
              for (int j = 0; j <= 3*w; ++j) {// 不购买第i个商品
                if (states[i-1][j] == true) states[i][j] = states[i-1][j];
              }
              for (int j = 0; j <= 3*w-items[i]; ++j) {//购买第i个商品
                if (states[i-1][j]==true) states[i][j+items[i]] = true;
              }
            }
          
            int j;
            for (j = w; j < 3*w+1; ++j) { 
              if (states[n-1][j] == true) break; // 输出结果大于等于w的最小值
            }
            if (j == 3*w+1) return; // 没有可行解
            for (int i = n-1; i >= 1; --i) { // i表示二维数组中的行，j表示列
              if(j-items[i] >= 0 && states[i-1][j-items[i]] == true) {
                System.out.print(items[i] + " "); // 购买这个商品
                j = j - items[i];
              } // else 没有购买这个商品，j不变。
            }
            if (j != 0) System.out.print(items[0]);
          }
          

          前半部分和其他的一样，主要看后半部分，状态 (i, j) 只有可能从 (i-1, j) 或者 (i-1, j-value[i]) 两个状态推导过来。所以，我们就检查这两个状态是否是可达的，也就是 states[i-1][j]或者 states[i-1][j-value[i]]是否是 true。

          如果 states[i-1][j]可达，就说明我们没有选择购买第 i 个商品，如果 states[i-1][j-value[i]]可达，那就说明我们选择了购买第 i 个商品。我们从中选择一个可达的状态（如果两个都可达，就随意选择一个），然后，继续迭代地考察其他商品是否有选择购买。

    • 从例子中，你应该能发现，大部分动态规划能解决的问题，都可以通过回溯算法来解决，只不过回溯算法解决起来效率比较低，时间复杂度是指数级的。动态规划算法，在执行效率方面，要高很多。尽管执行效率提高了，但是动态规划的空间复杂度也提高了，所以，很多时候，我们会说，动态规划是一种空间换时间的算法思想。

  • 动态规划理论

    • “一个模型三个特征”理论

      • 什么样的问题适合用动态规划来解决呢？换句话说，动态规划能解决的问题有什么规律可循呢？实际上，动态规划作为一个非常成熟的算法思想，很多人对此已经做了非常全面的总结。

      • 什么是“一个模型”？它指的是动态规划适合解决的问题的模型。我把这个模型定义为“多阶段决策最优解模型”。我们一般是用动态规划来解决最优问题。而解决问题的过程，需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

      • 现在，我们再来看，什么是“三个特征”？它们分别是最优子结构、无后效性和重复子问题。这三个概念比较抽象，我来逐一详细解释一下。

        1. 最优子结构

           最优子结构指的是，问题的最优解包含子问题的最优解。反过来说就是，我们可以通过子问题的最优解，推导出问题的最优解。如果我们把最优子结构，对应到我们前面定义的动态规划问题模型上，那我们也可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来。

        2. 无后效性

           无后效性有两层含义，第一层含义是，在推导后面阶段的状态的时候，我们只关心前面阶段的状态值，不关心这个状态是怎么一步一步推导出来的。第二层含义是，某阶段状态一旦确定，就不受之后阶段的决策影响。无后效性是一个非常“宽松”的要求。只要满足前面提到的动态规划问题模型，其实基本上都会满足无后效性。

        3. 重复子问题

           这个概念比较好理解。前面一节，我已经多次提过。如果用一句话概括一下，那就是，不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态。

    • “一个模型三个特征”实例剖析

      • 假设我们有一个 n 乘以 n 的矩阵 w[n][n]。矩阵存储的都是正整数。棋子起始位置在左上角，终止位置在右下角。我们将棋子从左上角移动到右下角。每次只能向右或者向下移动一位。从左上角到右下角，会有很多不同的路径可以走。我们把每条路径经过的数字加起来看作路径的长度。那从左上角移动到右下角的最短路径长度是多少呢？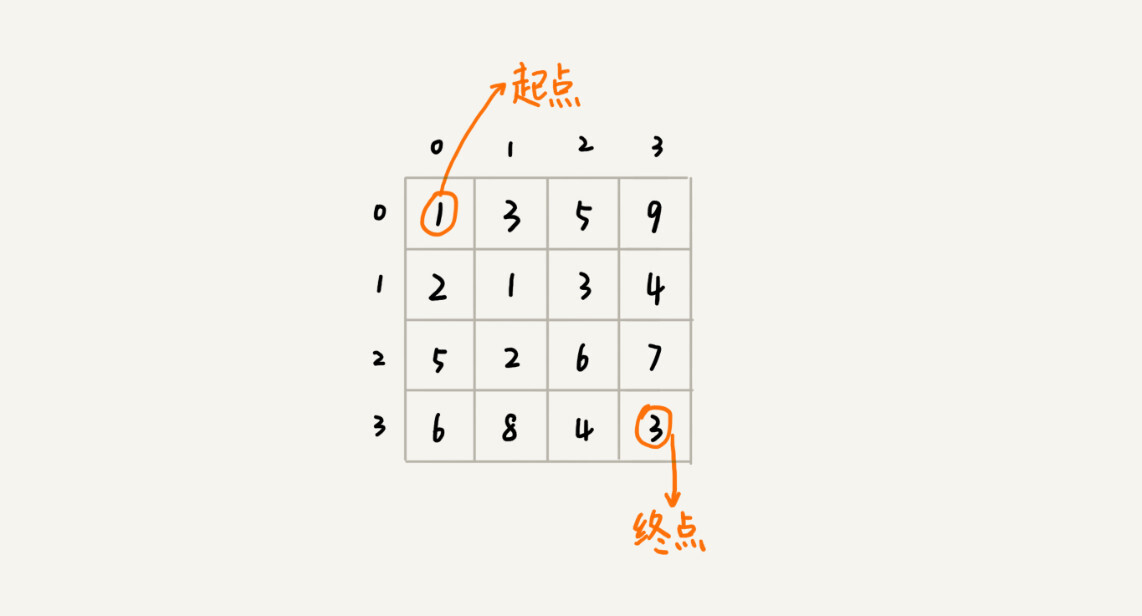

        

        我们先看看，这个问题是否符合“一个模型”？

        从 (0, 0) 走到 (n-1, n-1)，总共要走 2(n-1) 步，也就对应着 2(n-1) 个阶段。每个阶段都有向右走或者向下走两种决策，并且每个阶段都会对应一个状态集合。

        我们把状态定义为 min_dist(i, j)，其中 i 表示行，j 表示列。min_dist 表达式的值表示从 (0, 0) 到达 (i, j) 的最短路径长度。所以，这个问题是一个多阶段决策最优解问题，符合动态规划的模型。

        

        我们再来看，这个问题是否符合“三个特征”？

        我们可以用回溯算法来解决这个问题。如果你自己写一下代码，画一下递归树，就会发现，递归树中有重复的节点。重复的节点表示，从左上角到节点对应的位置，有多种路线，这也能说明这个问题中存在重复子问题。

        如果我们走到 (i, j) 这个位置，我们只能通过 (i-1, j)，(i, j-1) 这两个位置移动过来，也就是说，我们想要计算 (i, j) 位置对应的状态，只需要关心 (i-1, j)，(i, j-1) 两个位置对应的状态，并不关心棋子是通过什么样的路线到达这两个位置的。而且，我们仅仅允许往下和往右移动，不允许后退，所以，前面阶段的状态确定之后，不会被后面阶段的决策所改变，所以，这个问题符合“无后效性”这一特征。

        刚刚定义状态的时候，我们把从起始位置 (0, 0) 到 (i, j) 的最小路径，记作 min_dist(i, j)。因为我们只能往右或往下移动，所以，我们只有可能从 (i, j-1) 或者 (i-1, j) 两个位置到达 (i, j)。也就是说，到达 (i, j) 的最短路径要么经过 (i, j-1)，要么经过 (i-1, j)，而且到达 (i, j) 的最短路径肯定包含到达这两个位置的最短路径之一。换句话说就是，min_dist(i, j) 可以通过 min_dist(i, j-1) 和 min_dist(i-1, j) 两个状态推导出来。这就说明，这个问题符合“最优子结构”。

        min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

  • 两种动态规划解题思路总结

    1. 状态转移表法

       • 一般能用动态规划解决的问题，都可以使用回溯算法的暴力搜索解决。所以，当我们拿到问题的时候，我们可以先用简单的回溯算法解决，然后定义状态，每个状态表示一个节点，然后对应画出递归树。从递归树中，我们很容易可以看出来，是否存在重复子问题，以及重复子问题是如何产生的。以此来寻找规律，看是否能用动态规划解决。

       • 找到重复子问题之后，接下来，我们有两种处理思路，第一种是直接用回溯加“备忘录”的方法，来避免重复子问题。从执行效率上来讲，这跟动态规划的解决思路没有差别。第二种是使用动态规划的解决方法，状态转移表法。第一种思路，我就不讲了，你可以看看上一节的两个例子。我们重点来看状态转移表法是如何工作的。

       • 我们先画出一个状态表。状态表一般都是二维的，所以你可以把它想象成二维数组。其中，每个状态包含三个变量，行、列、数组值。我们根据决策的先后过程，从前往后，根据递推关系，分阶段填充状态表中的每个状态。最后，我们将这个递推填表的过程，翻译成代码，就是动态规划代码了。

       • 尽管大部分状态表都是二维的，但是如果问题的状态比较复杂，需要很多变量来表示，那对应的状态表可能就是高维的，比如三维、四维。那这个时候，我们就不适合用状态转移表法来解决了。一方面是因为高维状态转移表不好画图表示，另一方面是因为人脑确实很不擅长思考高维的东西。

       • 现在，我们来看一下，如何套用这个状态转移表法，来解决之前那个矩阵最短路径的问题？

       • 从起点到终点，我们有很多种不同的走法。我们可以穷举所有走法，然后对比找出一个最短走法。不过如何才能无重复又不遗漏地穷举出所有走法呢？我们可以用回溯算法这个比较有规律的穷举算法。

       • 回溯算法的代码实现如下所示。代码很短，而且我前面也分析过很多回溯算法的例题，这里我就不多做解释了，你自己来看看。

         private int minDist = Integer.MAX_VALUE; // 全局变量或者成员变量
         // 调用方式：minDistBacktracing(0, 0, 0, w, n);
         public void minDistBT(int i, int j, int dist, int[][] w, int n) {
           // 到达了n-1, n-1这个位置了，这里看着有点奇怪哈，你自己举个例子看下
           if (i == n && j == n) {
             if (dist < minDist) minDist = dist;
             return;
           }
           if (i < n) { // 往下走，更新i=i+1, j=j
             minDistBT(i + 1, j, dist+w[i][j], w, n);
           }
           if (j < n) { // 往右走，更新i=i, j=j+1
             minDistBT(i, j+1, dist+w[i][j], w, n);
           }
         }
         

       • 有了回溯代码之后，接下来，我们要画出递归树，以此来寻找重复子问题。在递归树中，一个状态（也就是一个节点）包含三个变量 (i, j, dist)，其中 i，j 分别表示行和列，dist 表示从起点到达 (i, j) 的路径长度。从图中，我们看出，尽管 (i, j, dist) 不存在重复的，但是 (i, j) 重复的有很多。对于 (i, j) 重复的节点，我们只需要选择 dist 最小的节点，继续递归求解，其他节点就可以舍弃了。

         

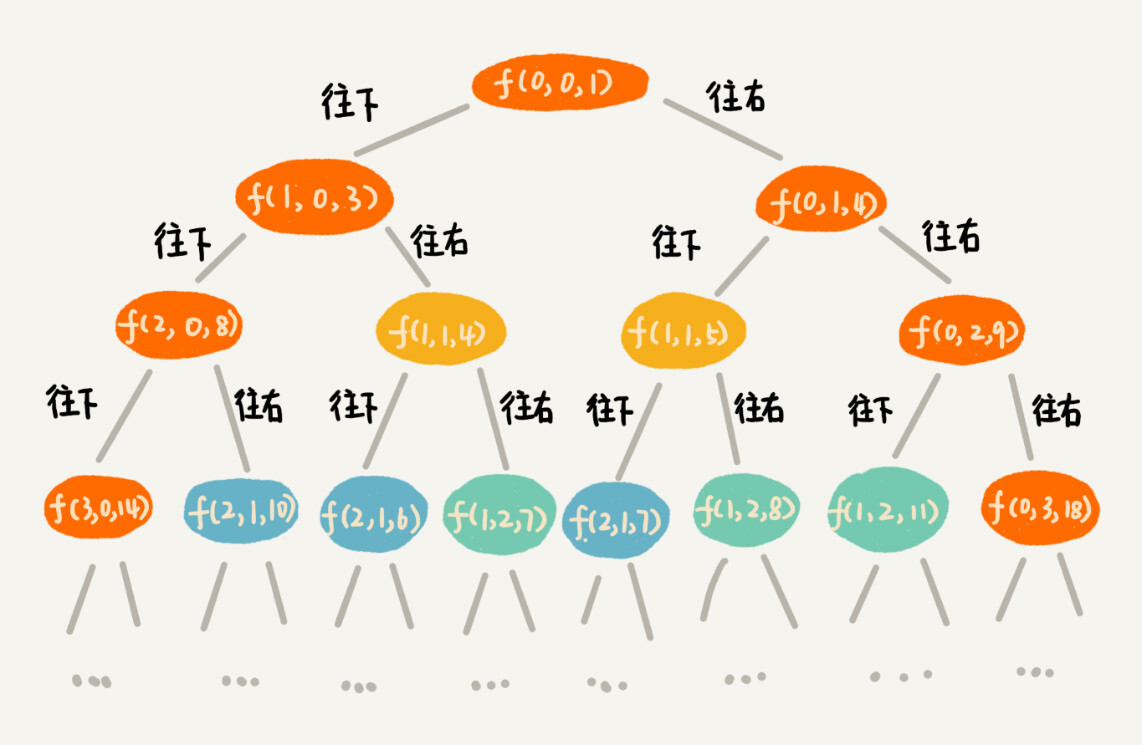
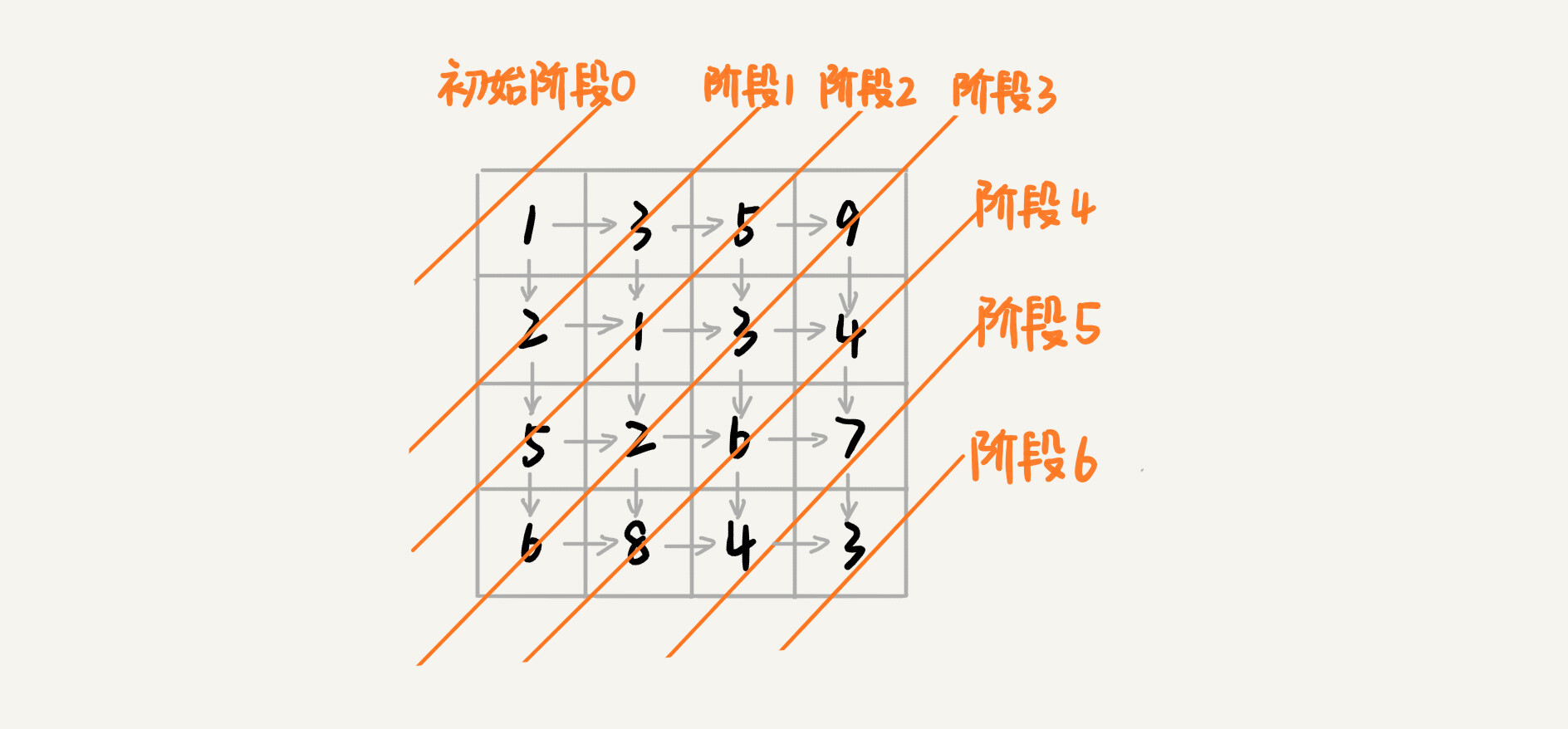
       • 我们画出一个二维状态表，表中的行、列表示棋子所在的位置，表中的数值表示从起点到这个位置的最短路径。我们按照决策过程，通过不断状态递推演进，将状态表填好。为了方便代码实现，我们按行来进行依次填充。

         

         

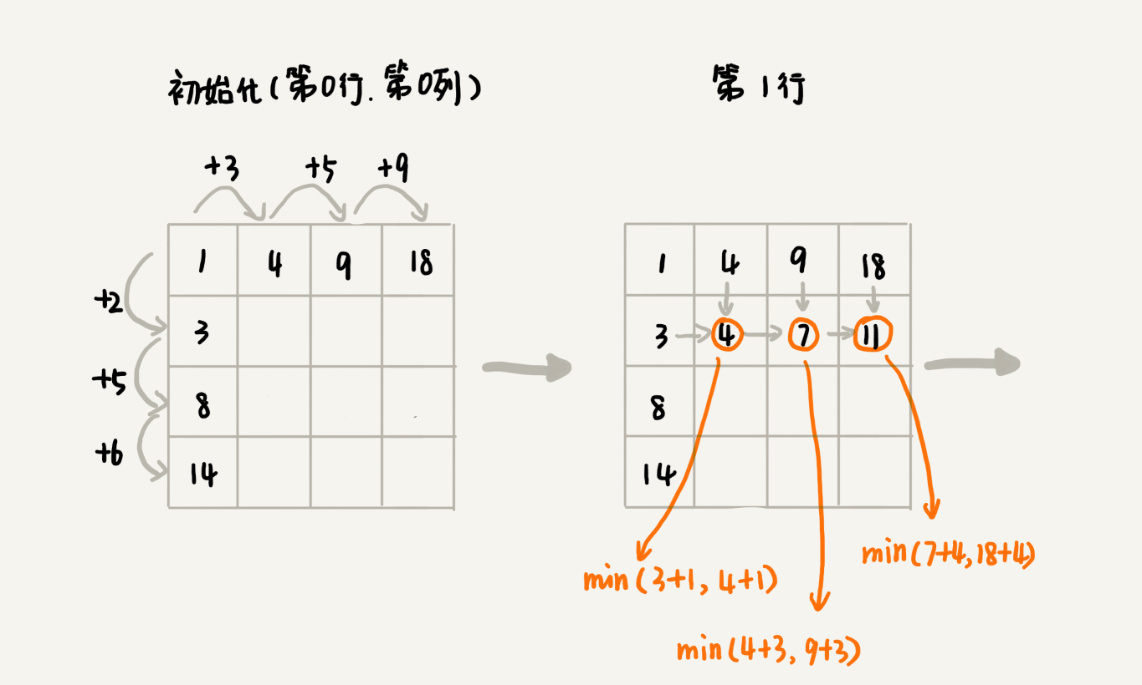
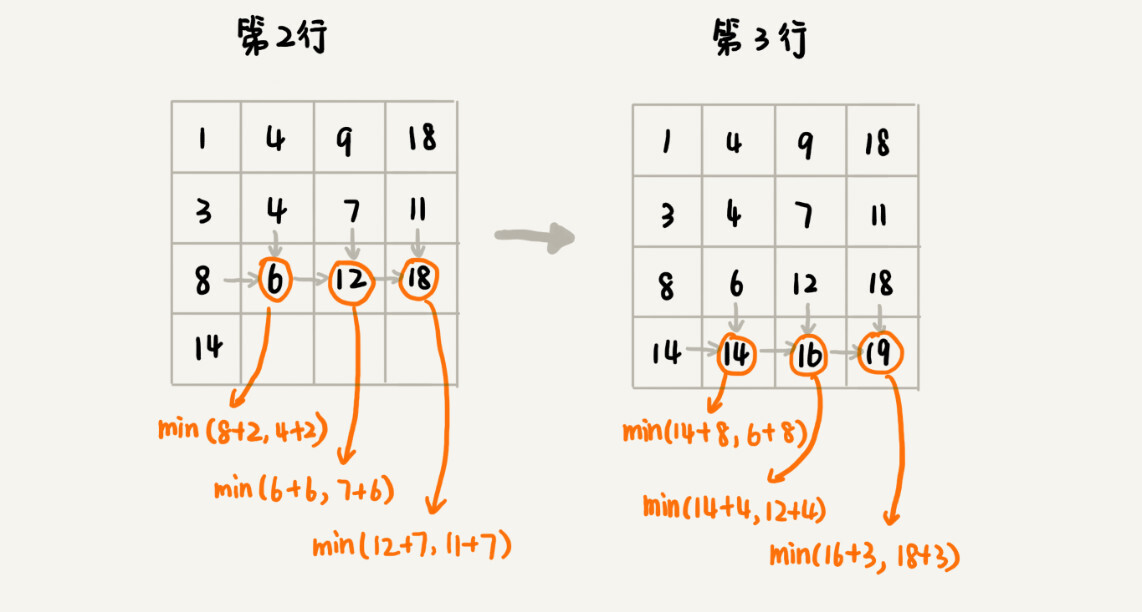
       • 弄懂了填表的过程，代码实现就简单多了。我们将上面的过程，翻译成代码，就是下面这个样子。结合着代码、图和文字描述，应该更容易理解我讲的内容。

         
         public int minDistDP(int[][] matrix, int n) {
           int[][] states = new int[n][n];
           int sum = 0;
           for (int j = 0; j < n; ++j) { // 初始化states的第一行数据
             sum += matrix[0][j];
             states[0][j] = sum;
           }
           sum = 0;
           for (int i = 0; i < n; ++i) { // 初始化states的第一列数据
             sum += matrix[i][0];
             states[i][0] = sum;
           }
           for (int i = 1; i < n; ++i) {
             for (int j = 1; j < n; ++j) {
               states[i][j] = 
                     matrix[i][j] + Math.min(states[i][j-1], states[i-1][j]);
             }
           }
           return states[n-1][n-1];
         }
         

       • 状态转移表法解题思路大致可以概括为，回溯算法实现 - 定义状态 - 画递归树 - 找重复子问题 - 画状态转移表 - 根据递推关系填表 - 将填表过程翻译成代码。

    2. 状态转移方程法

       • 状态转移方程法有点类似递归的解题思路。我们需要分析，某个问题如何通过子问题来递归求解，也就是所谓的最优子结构。根据最优子结构，写出递归公式，也就是所谓的状态转移方程。有了状态转移方程，代码实现就非常简单了。一般情况下，我们有两种代码实现方法，一种是递归加“备忘录”，另一种是迭代递推。

       • 我们还是拿刚才的例子来举例。最优子结构前面已经分析过了，你可以回过头去再看下。为了方便你查看，我把状态转移方程放到这里。

         min_dist(i, j) = w[i][j] + min(min_dist(i, j-1), min_dist(i-1, j))

       • 这里我强调一下，状态转移方程是解决动态规划的关键。如果我们能写出状态转移方程，那动态规划问题基本上就解决一大半了，而翻译成代码非常简单。但是很多动态规划问题的状态本身就不好定义，状态转移方程也就更不好想到。

       • 下面我用递归加“备忘录”的方式，将状态转移方程翻译成来代码，你可以看看。对于另一种实现方式，跟状态转移表法的代码实现是一样的，只是思路不同。

         private int[][] matrix = 
                  {{1，3，5，9}, {2，1，3，4}，{5，2，6，7}，{6，8，4，3}};
         private int n = 4;
         private int[][] mem = new int[4][4];
         public int minDist(int i, int j) { // 调用minDist(n-1, n-1);
           if (i == 0 && j == 0) return matrix[0][0];
           if (mem[i][j] > 0) return mem[i][j];
           int minLeft = Integer.MAX_VALUE;
           if (j-1 >= 0) {
             minLeft = minDist(i, j-1);
           }
           int minUp = Integer.MAX_VALUE;
           if (i-1 >= 0) {
             minUp = minDist(i-1, j);
           }
           
           int currMinDist = matrix[i][j] + Math.min(minLeft, minUp);
           mem[i][j] = currMinDist;
           return currMinDist;
         }
         

       • 两种动态规划解题思路到这里就讲完了。我要强调一点，不是每个问题都同时适合这两种解题思路。有的问题可能用第一种思路更清晰，而有的问题可能用第二种思路更清晰，所以，你要结合具体的题目来看，到底选择用哪种解题思路。

       • 状态转移方程法的大致思路可以概括为，找最优子结构 - 写状态转移方程 - 将状态转移方程翻译成代码。

  • 动态规划实战

    • 我们有一个数字序列包含 n 个不同的数字，如何求出这个序列中的最长递增子序列长度？比如 2, 9, 3, 6, 5, 1, 7 这样一组数字序列，它的最长递增子序列就是 2, 3, 5, 7，所以最长递增子序列的长度是 4。

    • 思路

      // 递推公式: lss_lengths[i] = max(condition: j < i && a[j] < a[i] value: lss_lengths[j] + 1)
      // 动态规划求 a 的最上升长子序列长度
      int longestSubsequence(int[] num, int n) 
      {
          // 创建一个数组, 索引 i 对应考察元素的下标, 存储 arr[0...i] 的最长上升子序列大小
          int[] lss_lengths = new int[n];
          // 第一个元素哨兵处理
          lss_lengths[0] = 1;
          // 动态规划求解最长子序列
          int i, j, max;
          for (i = 1; i < n; i++) {
              // 计算 arr[0...i] 的最长上升子序列
              // 递推公式: lss_lengths[i] = max(condition: j < i && a[j] < a[i] value: lss_lengths[j] + 1)
              max = 1;
              for (j = 0; j < i; j++) {
                  if (num[i] > num[j] && lss_lengths[j] >= max) {
                      max = lss_lengths[j] + 1;
                  }
              }
              lss_lengths[i] = max;
          }
          int lss_length = lss_lengths[n - 1];
          return lss_length;
      }
      

• 四种算法思想比较分析

  • 我们已经学习了四种算法思想，贪心、分治、回溯和动态规划，它们之间有什么区别和联系呢。
  • 如果我们将这四种算法思想分一下类，那贪心、回溯、动态规划可以归为一类，而分治单独可以作为一类，因为它跟其他三个都不大一样。为什么这么说呢？前三个算法解决问题的模型，都可以抽象成我们今天讲的那个多阶段决策最优解模型，而分治算法解决的问题尽管大部分也是最优解问题，但是，大部分都不能抽象成多阶段决策模型。
  • 回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决。回溯算法相当于穷举搜索。穷举所有的情况，然后对比得到最优解。不过，回溯算法的时间复杂度非常高，是指数级别的，只能用来解决小规模数据的问题。对于大规模数据的问题，用回溯算法解决的执行效率就很低了。
  • 尽管动态规划比回溯算法高效，但是，并不是所有问题，都可以用动态规划来解决。能用动态规划解决的问题，需要满足三个特征，最优子结构、无后效性和重复子问题。在重复子问题这一点上，动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题，不能有重复子问题，而动态规划正好相反，动态规划之所以高效，就是因为回溯算法实现中存在大量的重复子问题。
  • 贪心算法实际上是动态规划算法的一种特殊情况。它解决问题起来更加高效，代码实现也更加简洁。不过，它可以解决的问题也更加有限。它能解决的问题需要满足三个条件，最优子结构、无后效性和贪心选择性（这里我们不怎么强调重复子问题）。
  • 其中，最优子结构、无后效性跟动态规划中的无异。“贪心选择性”的意思是，通过局部最优的选择，能产生全局的最优选择。每一个阶段，我们都选择当前看起来最优的决策，所有阶段的决策完成之后，最终由这些局部最优解构成全局最优解。

参考资料

• 数据结构与算法之美
• 数据结构和算法必知必会的50个代码实现