数据结构与算法知识树整理——算法篇——排序
算法知识树整理
排序
-
- 排序算法的执行效率
- 最好情况、最坏情况、平均情况时间复杂度
- 时间复杂度的系数、常数 、低阶
- 比较次数和交换(或移动)次数
- 排序算法的内存消耗
- 原地排序(Sorted in place)。原地排序算法,就是特指空间复杂度是 O(1) 的排序算法。
- 排序算法的稳定性
- 稳定性。这个概念是说,如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
- 排序算法的执行效率
-
-
我用一个例子,带你看下冒泡排序的整个过程。我们要对一组数据 4,5,6,3,2,1,从小到大进行排序。第一次冒泡操作的详细过程就是这样:
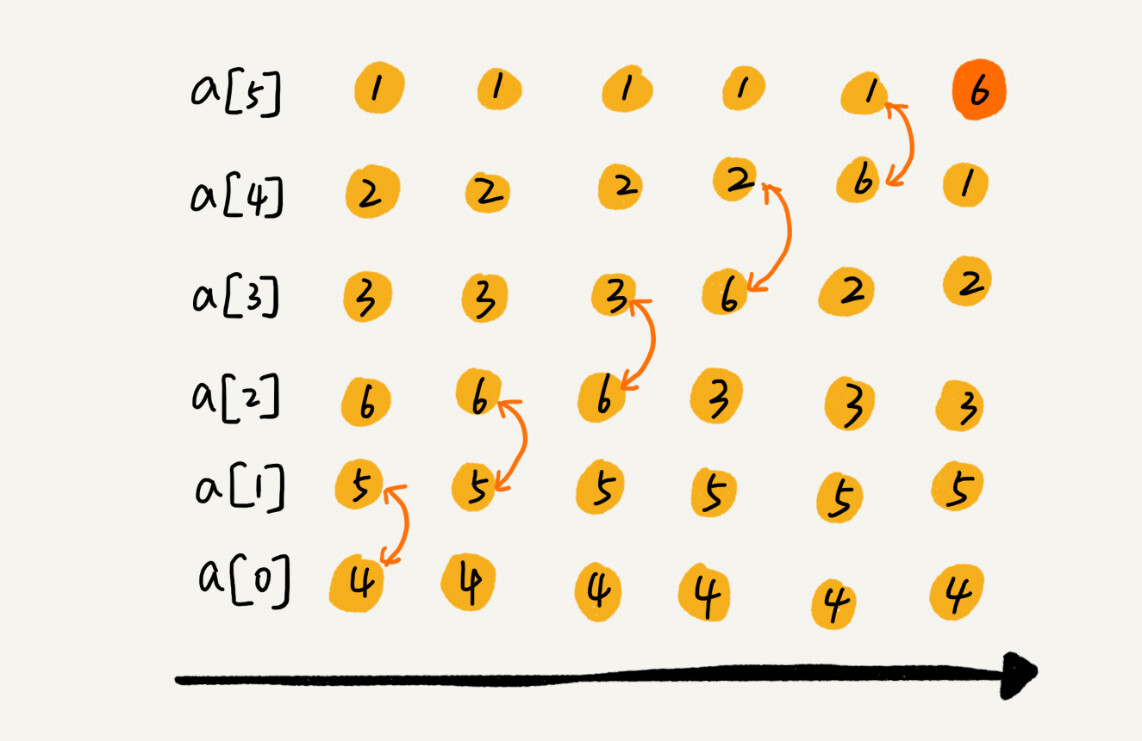
可以看出,经过一次冒泡操作之后,6 这个元素已经存储在正确的位置上。要想完成所有数据的排序,我们只要进行 6 次这样的冒泡操作就行了

实际上,刚讲的冒泡过程还可以优化。当某次冒泡操作已经没有数据交换时,说明已经达到完全有序,不用再继续执行后续的冒泡操作。我这里还有另外一个例子,这里面给 6 个元素排序,只需要 4 次冒泡操作就可以了。
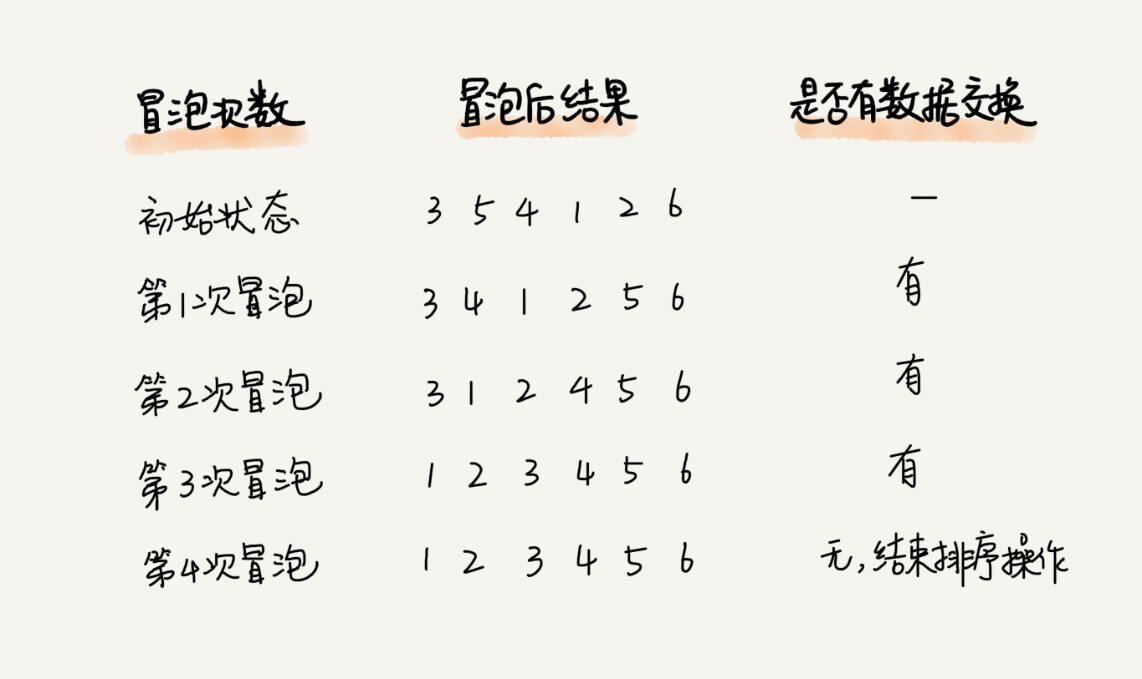
// 冒泡排序,a表示数组,n表示数组大小 public void bubbleSort(int[] a, int n) { if (n <= 1) return; for (int i = 0; i < n; ++i) { // 提前退出冒泡循环的标志位 boolean flag = false; for (int j = 0; j < n - i - 1; ++j) { if (a[j] > a[j+1]) { // 交换 int tmp = a[j]; a[j] = a[j+1]; a[j+1] = tmp; flag = true; // 表示有数据交换 } } if (!flag) break; // 没有数据交换,提前退出 } } -
冒泡排序是原地排序算法吗?
冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为 O(1),是一个原地排序算法。
-
冒泡排序是稳定的排序算法吗?
在冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。
-
冒泡排序的时间复杂度是多少?
- 最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束了,所以最好情况时间复杂度是 O(n)。
- 最坏的情况是,要排序的数据刚好是倒序排列的,我们需要进行 n 次冒泡操作,所以最坏情况时间复杂度为 O(n2)。
- 平均情况下的时间复杂度就是 O(n2)。
-
-
-
一个有序的数组,我们往里面添加一个新的数据后,如何继续保持数据有序呢?很简单,我们只要遍历数组,找到数据应该插入的位置将其插入即可。
-
我们将数组中的数据分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。

-
插入排序也包含两种操作,一种是元素的比较,一种是元素的移动。
// 插入排序,a表示数组,n表示数组大小 public void insertionSort(int[] a, int n) { if (n <= 1) return; for (int i = 1; i < n; ++i) { int value = a[i]; int j = i - 1; // 查找插入的位置 for (; j >= 0; --j) { if (a[j] > value) { a[j+1] = a[j]; // 数据移动 } else { break; } } a[j+1] = value; // 插入数据 } } -
插入排序是原地排序算法吗?
从实现过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是 O(1),也就是说,这是一个原地排序算法。
-
插入排序是稳定的排序算法吗?
在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法
-
插入排序的时间复杂度是多少?
最好是时间复杂度为 O(n)
最坏情况时间复杂度为 O(n^2)。
平均时间复杂度为 O(n^2)。
-
冒泡排序和插入排序的时间复杂度都是 O(n2),都是原地排序算法,为什么插入排序要比冒泡排序更受欢迎呢?
-
冒泡排序不管怎么优化,元素交换的次数是一个固定值,是原始数据的逆序度。插入排序是同样的,不管怎么优化,元素移动的次数也等于原始数据的逆序度。
-
但是,从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要 3 个赋值操作,而插入排序只需要 1 个。我们来看这段操作:
冒泡排序中数据的交换操作: if (a[j] > a[j+1]) { // 交换 int tmp = a[j]; a[j] = a[j+1]; a[j+1] = tmp; flag = true; } 插入排序中数据的移动操作: if (a[j] > value) { a[j+1] = a[j]; // 数据移动 } else { break; }我们把执行一个赋值语句的时间粗略地计为单位时间(unit_time),然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序,需要 K 次交换操作,每次需要 3 个赋值语句,所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。
针对上面的冒泡排序和插入排序的 Java 代码,我写了一个性能对比测试程序,随机生成 10000 个数组,每个数组中包含 200 个数据,然后在我的机器上分别用冒泡和插入排序算法来排序,冒泡排序算法大约 700ms 才能执行完成,而插入排序只需要 100ms 左右就能搞定!
-
-
-
-
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
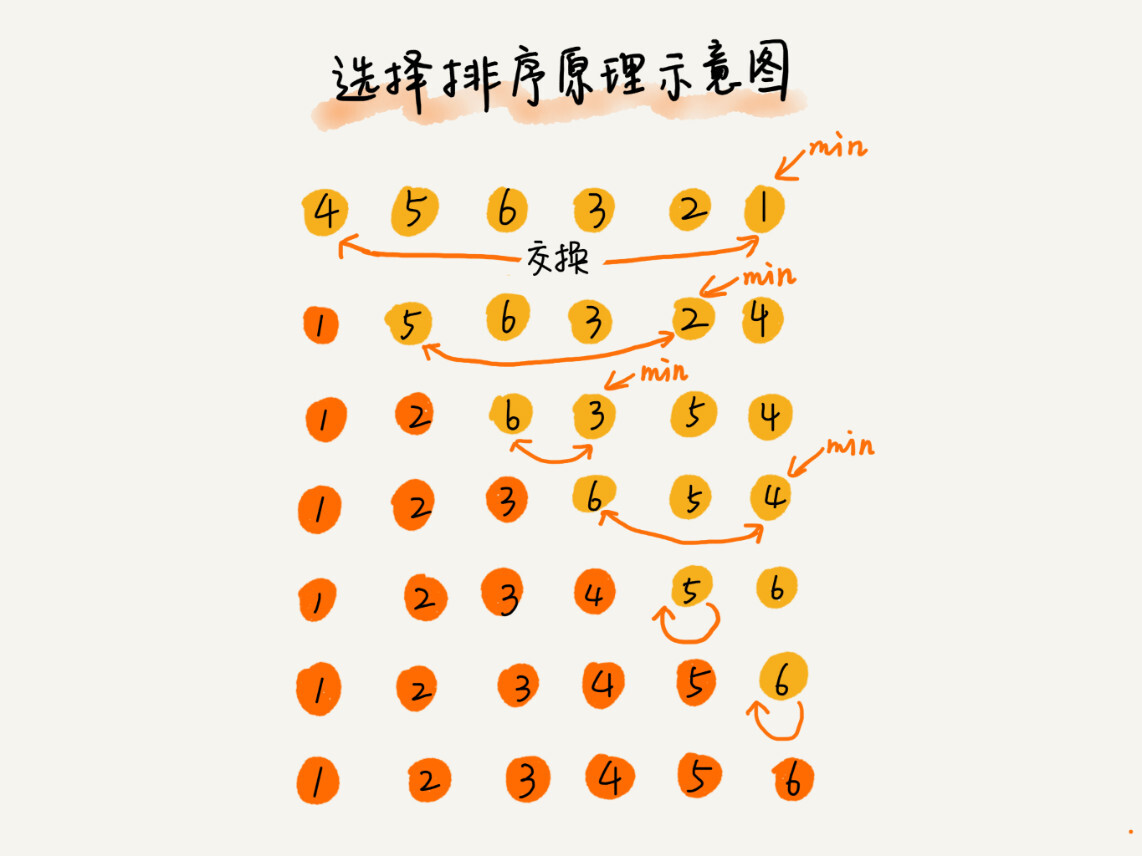
-
选择排序的时间复杂度是多少?
最好是时间复杂度为 O(n)
最坏情况时间复杂度为 O(n^2)。
平均时间复杂度为 O(n^2)。
-
选择排序是稳定的排序算法吗?
选择排序是一种不稳定的排序算法。从我前面画的那张图中,你可以看出来,选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样破坏了稳定性。
-
-
-
归并排序的核心思想还是蛮简单的。如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
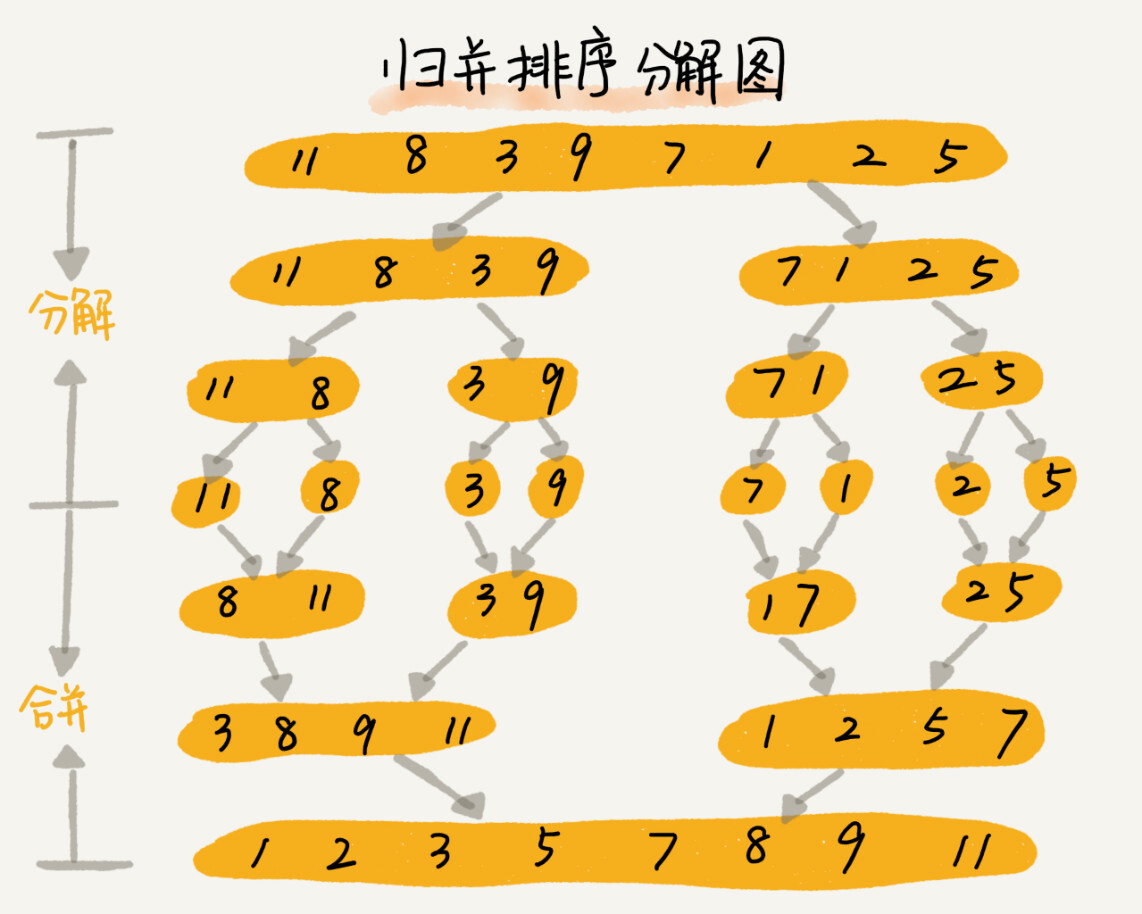
-
归并排序使用的就是分治思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
-
我们先写出归并排序的递推公式。
递推公式: merge_sort(p…r) = merge(merge_sort(p…q),merge_sort(q+1…r)) 终止条件:p >= r 不用再继续分解 -
merge_sort(p…r) 表示,给下标从 p 到 r 之间的数组排序。我们将这个排序问题转化为了两个子问题,merge_sort(p…q) 和 merge_sort(q+1…r),其中下标 q 等于 p 和 r 的中间位置,也就是 (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后,我们再将两个有序的子数组合并在一起,这样下标从 p 到 r 之间的数据就也排好序了
-
如图所示,我们申请一个临时数组 tmp,大小与 A[p...r]相同。我们用两个游标 i 和 j,分别指向 A[p...q]和 A[q+1...r]的第一个元素。比较这两个元素 A[i]和 A[j],如果 A[i]<=A[j],我们就把 A[i]放入到临时数组 tmp,并且 i 后移一位,否则将 A[j]放入到数组 tmp,j 后移一位。
-
继续上述比较过程,直到其中一个子数组中的所有数据都放入临时数组中,再把另一个数组中的数据依次加入到临时数组的末尾,这个时候,临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p...r]中。
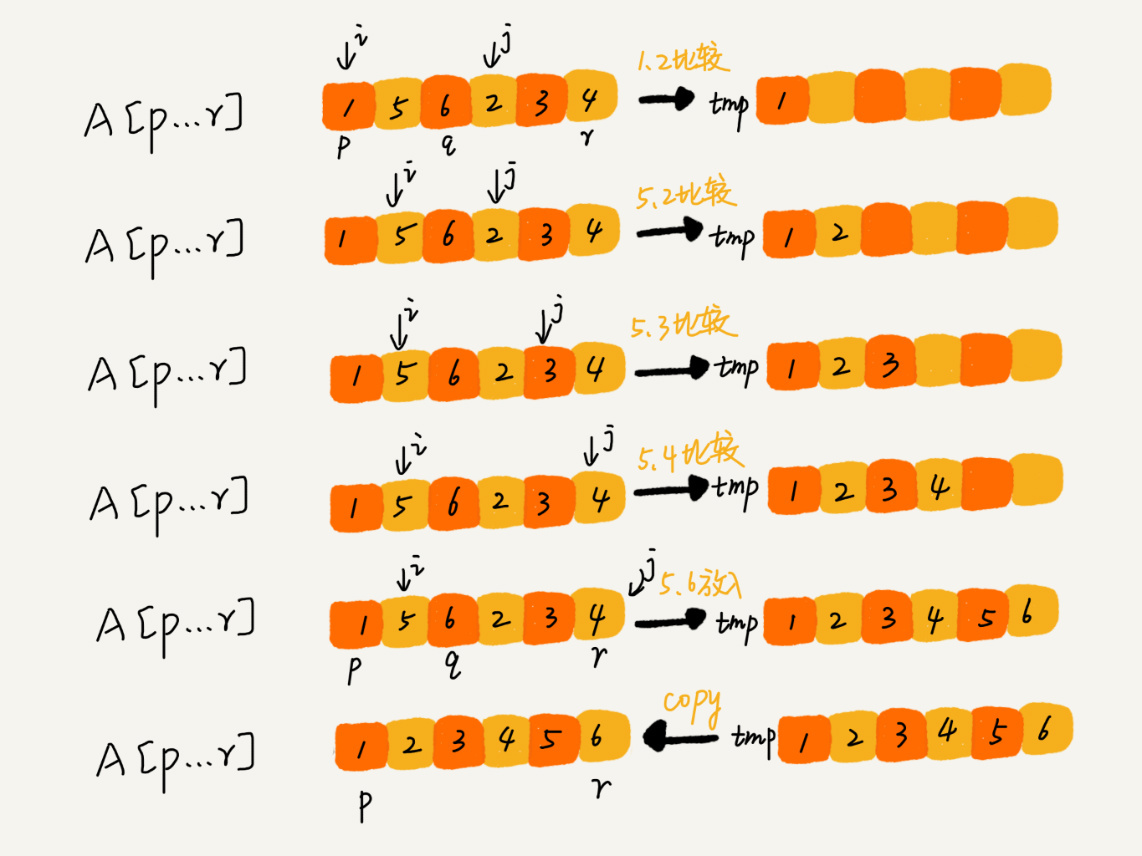
public class Solution { public int Main(int[] nums) { MergeSort(nums,0, nums.Length-1); } public void MergeSort(int[] arr, int min,int max) { if (min > max) return; int mid = min + (max - min ) / 2;//防止加法溢出 MergeSort(arr, min, mid);//由下往上 MergeSort(arr, mid + 1, max); Merge(arr, min, mid, mid + 1, max); } public void Merge(int[] arr,int leftMin, int leftMax, int rightMin, int rightMax) { int i = leftMin; int j = rightMin; int idx = 0; int[] newArr = new int[(leftMax-leftMin + 1) + (rightMax-rightMin + 1)]; while (i <= leftMax && j <= rightMax) { if (arr[i] < arr[j]) newArr[idx++] = arr[i++]; else newArr[idx++] = arr[j++]; } while (i <= leftMax) { newArr[idx++] = arr[i++]; } while (j <= rightMax) { newArr[idx++] = arr[j++]; } for (int k = 0; k < newArr.Length; k++) { arr[leftMin + k] = newArr[k]; } } } -
归并排序的性能分析
-
第一,归并排序是稳定的排序算法吗?
在合并的过程中,如果 A[p...q]和 A[q+1...r]之间有值相同的元素,那我们可以像伪代码中那样,先把 A[p...q]中的元素放入 tmp 数组。这样就保证了值相同的元素,在合并前后的先后顺序不变。所以,归并排序是一个稳定的排序算法。
-
第二,归并排序的时间复杂度是多少?
- 归并排序的时间复杂度是 O(nlogn)。
-
-
归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。.
-
第三,归并排序的空间复杂度是多少?
在合并两个有序数组为一个有序数组时,需要借助额外的存储空间,空间复杂度是 O(n)。
-
-
-
快排的思想
-
快排利用的也是分治思想。乍看起来,它有点像归并排序,但是思路其实完全不一样。
-
快排核心思想就是分治和分区
-
如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。
-
我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
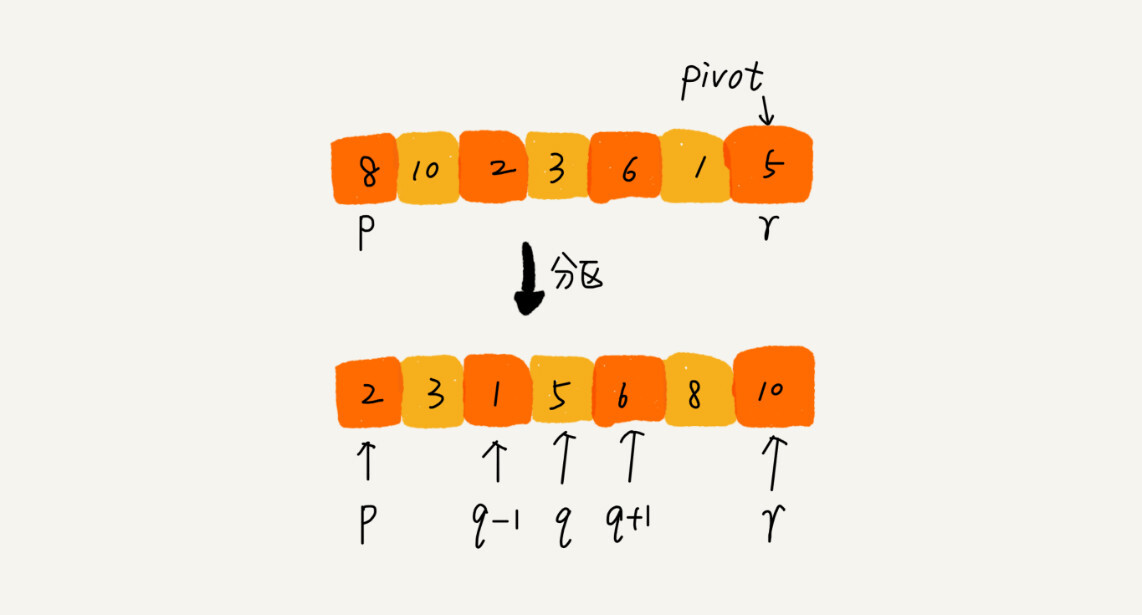
-
根据分治、递归的处理思想,我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
-
归并排序中有一个 merge() 合并函数,我们这里有一个 partition() 分区函数。partition() 分区函数实际上我们前面已经讲过了,就是随机选择一个元素作为 pivot(一般情况下,可以选择 p 到 r 区间的最后一个元素),然后对 A[p...r]分区,函数返回 pivot 的下标。
-
如果我们不考虑空间消耗的话,partition() 分区函数可以写得非常简单。我们申请两个临时数组 X 和 Y,遍历 A[p...r],将小于 pivot 的元素都拷贝到临时数组 X,将大于 pivot 的元素都拷贝到临时数组 Y,最后再将数组 X 和数组 Y 中数据顺序拷贝到 A[p....r]。
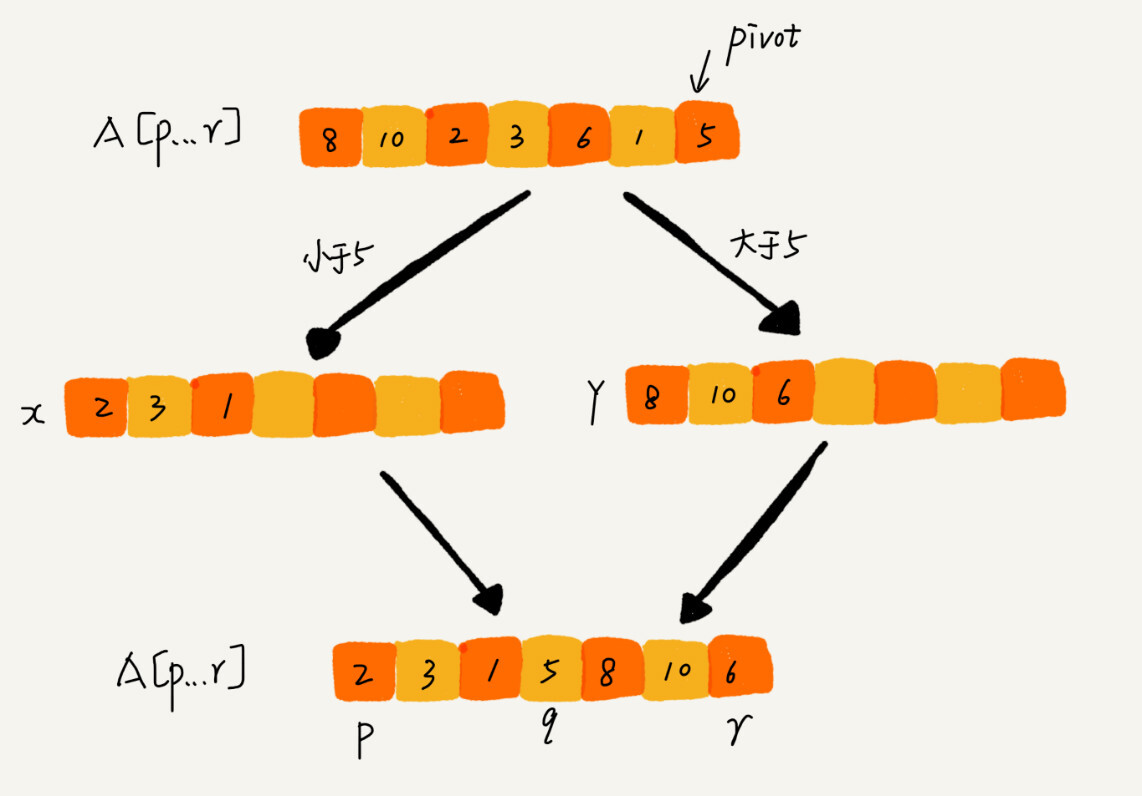
但是,如果按照这种思路实现的话,partition() 函数就需要很多额外的内存空间,所以快排就不是原地排序算法了。如果我们希望快排是原地排序算法,那它的空间复杂度得是 O(1),那 partition() 分区函数就不能占用太多额外的内存空间,我们就需要在 A[p...r]的原地完成分区操作。
-
原地分区函数的实现思路非常巧妙,处理有点类似选择排序。我们通过游标 i 把 A[p...r-1]分成两部分。A[p...i-1]的元素都是小于 pivot 的,我们暂且叫它“已处理区间”,A[i...r-1]是“未处理区间”。我们每次都从未处理的区间 A[i...r-1]中取一个元素 A[j],与 pivot 对比,如果小于 pivot,则将其加入到已处理区间的尾部,也就是 A[i]的位置。
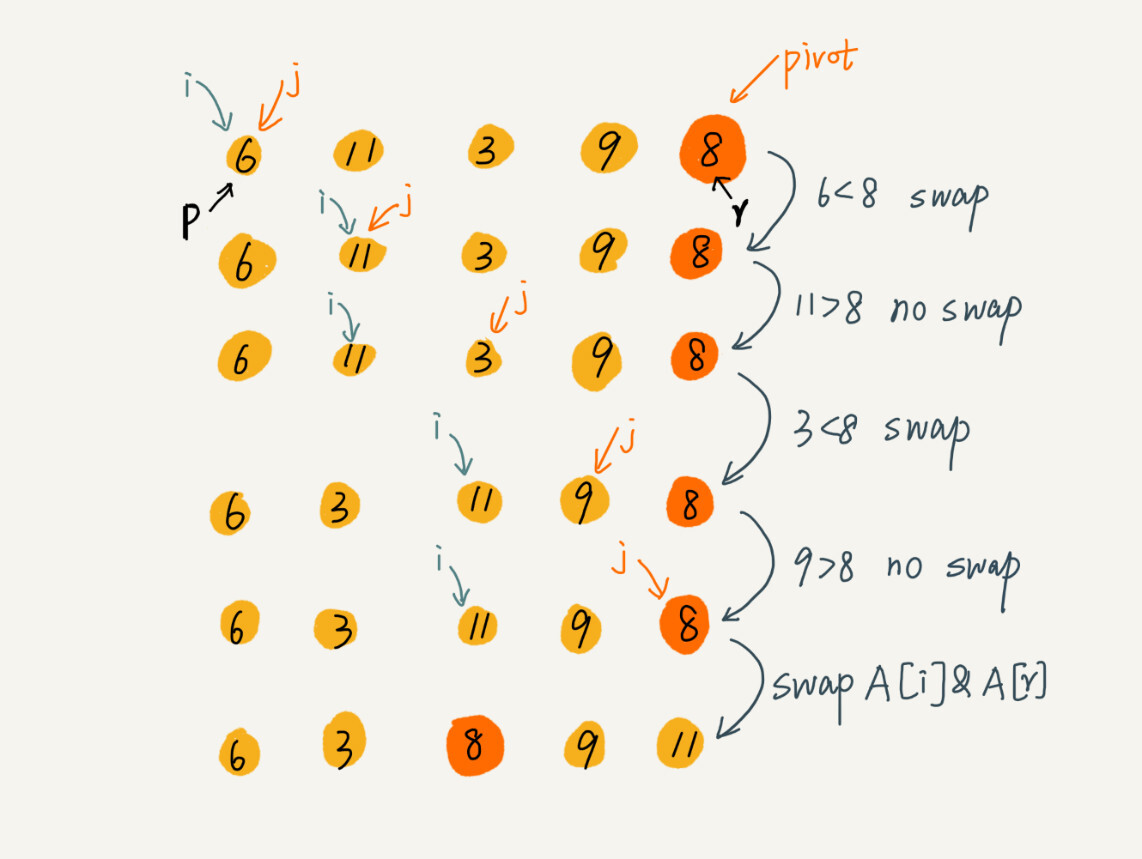
-
代码如下
private void QuickSort(int[] arr,int start,int end, int flagIdx) { if (start > end) return; int mid = Partition(arr, start, end, flagIdx); QuickSort(arr, start, mid-1,mid-1); QuickSort(arr, mid+1, end,end); } private int Partition(int[] arr,int start,int end, int flagIdx) { int i = start; int j = start; while (j <= end) { if (arr[j] < arr[flagIdx]) { Swap(arr, i, j); i++; } j++; } Swap(arr, i, flagIdx); return i; } private void Swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; }
-
-
我再来看另外一个问题:快排和归并用的都是分治思想,递推公式和递归代码也非常相似,那它们的区别在哪里呢?
可以发现,归并排序的处理过程是由下到上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
-
快速排序的性能分析
- 快排的时间复杂度是 O(nlogn)。
- 如果数组中的数据原来已经是有序的了,比如 1,3,5,6,8。如果我们每次选择最后一个元素作为 pivot,那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作,才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素,这种情况下,快排的时间复杂度就从 O(nlogn) 退化成了 O(n^2)。
- 在大部分情况下的时间复杂度都可以做到 O(nlogn),只有在极端情况下,才会退化到 O(n2)。而且,我们也有很多方法将这个概率降到很低,如何来做?
-
来解答开篇的问题:O(n) 时间复杂度内求无序数组中的第 K 大元素。比如,4, 2, 5, 12, 3 这样一组数据,
-
思路
- 利用快排思想,先分区一次,判断flag是否是倒数第K个,如果是就over
- 如果小于K就代表第K个元素在大于flag的半区,去那个半区搜
- 如果大于k就代表k个元素在小于flag的半区,去另一个半区搜
- 递归
-
代码实现
public class Solution { public int FindKthLargest(int[] nums, int k) { return QuickFind(nums,0, nums.Length-1, nums.Length-1,nums.Length - k); } private int QuickFind(int[] arr,int start,int end, int flagIdx,int findIdx) { if (start > end) throw new Exception("no find idx"); int mid = Partition(arr, start, end, flagIdx); if (mid == findIdx) { return arr[mid]; } else if(mid > findIdx) { return QuickFind(arr, start, mid - 1, mid - 1, findIdx); } else { return QuickFind(arr, mid + 1, end, end, findIdx); } } private int Partition(int[] arr,int start,int end, int flagIdx) { int i = start; int j = start; while (j <= end) { if (arr[j] < arr[flagIdx]) { Swap(arr, i, j); i++; } j++; } Swap(arr, i, flagIdx); return i; } private void Swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } }
-
课后习题
现在你有 10 个接口访问日志文件,每个日志文件大小约 300MB,每个文件里的日志都是按照时间戳从小到大排序的。你希望将这 10 个较小的日志文件,合并为 1 个日志文件,合并之后的日志仍然按照时间戳从小到大排列。如果处理上述排序任务的机器内存只有 1GB,你有什么好的解决思路,能“快速”地将这 10 个日志文件合并吗?
- 思路
- 创建10个IO流,每个文件读第一条,比较出最小的,写入
- 写入后在从那个文件流在读一条,重复上述操作
-
-
-
原理
-
首先,我们来看桶排序。桶排序,顾名思义,会用到“桶”,核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。

-
如果要排序的数据有 n 个,我们把它们均匀地划分到 m 个桶内,每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序,时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk),因为 k=n/m,所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时,log(n/m) 就是一个非常小的常量,这个时候桶排序的时间复杂度接近 O(n)。
-
-
桶排序看起来很优秀,那它是不是可以替代我们之前讲的排序算法呢?
-
答案当然是否定的。为了让你轻松理解桶排序的核心思想,我刚才做了很多假设。实际上,桶排序对要排序数据的要求是非常苛刻的。
-
首先,要排序的数据需要很容易就能划分成 m 个桶,并且,桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后,桶与桶之间的数据不需要再进行排序。
-
其次,数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后,有些桶里的数据非常多,有些非常少,很不平均,那桶内数据排序的时间复杂度就不是常量级了。在极端情况下,如果数据都被划分到一个桶里,那就退化为 O(nlogn) 的排序算法了。
-
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
比如说我们有 10GB 的订单数据,我们希望按订单金额(假设金额都是正整数)进行排序,但是我们的内存有限,只有几百 MB,没办法一次性把 10GB 的数据都加载到内存中。这个时候该怎么办呢?
- 我们可以先扫描一遍文件,看订单金额所处的数据范围。假设经过扫描之后我们得到,订单金额最小是 1 元,最大是 10 万元。我们将所有订单根据金额划分到 100 个桶里,第一个桶我们存储金额在 1 元到 1000 元之内的订单,第二桶存储金额在 1001 元到 2000 元之内的订单,以此类推。每一个桶对应一个文件,并且按照金额范围的大小顺序编号命名(00,01,02...99)。
- 理想的情况下,如果订单金额在 1 到 10 万之间均匀分布,那订单会被均匀划分到 100 个文件中,每个小文件中存储大约 100MB 的订单数据,我们就可以将这 100 个小文件依次放到内存中,用快排来排序。等所有文件都排好序之后,我们只需要按照文件编号,从小到大依次读取每个小文件中的订单数据,并将其写入到一个文件中,那这个文件中存储的就是按照金额从小到大排序的订单数据了。
- 不过,你可能也发现了,订单按照金额在 1 元到 10 万元之间并不一定是均匀分布的 ,所以 10GB 订单数据是无法均匀地被划分到 100 个文件中的。有可能某个金额区间的数据特别多,划分之后对应的文件就会很大,没法一次性读入内存。这又该怎么办呢?
- 针对这些划分之后还是比较大的文件,我们可以继续划分,比如,订单金额在 1 元到 1000 元之间的比较多,我们就将这个区间继续划分为 10 个小区间,1 元到 100 元,101 元到 200 元,201 元到 300 元....901 元到 1000 元。如果划分之后,101 元到 200 元之间的订单还是太多,无法一次性读入内存,那就继续再划分,直到所有的文件都能读入内存为止。
-
-
-
-
原理
- 计数排序其实是桶排序的一种特殊情况。
- 当要排序的 n 个数据,所处的范围并不大的时候,比如最大值是 k,我们就可以把数据划分成 k 个桶。每个桶内的数据值都是相同的,省掉了桶内排序的时间。
- 如高考的例子:
- 我们都经历过高考,高考查分数系统你还记得吗?我们查分数的时候,系统会显示我们的成绩以及所在省的排名。如果你所在的省有 50 万考生,如何通过成绩快速排序得出名次呢?
- 考生的满分是 900 分,最小是 0 分,这个数据的范围很小,所以我们可以分成 901 个桶,对应分数从 0 分到 900 分。根据考生的成绩,我们将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生,所以并不需要再进行排序。我们只需要依次扫描每个桶,将桶内的考生依次输出到一个数组中,就实现了 50 万考生的排序。因为只涉及扫描遍历操作,所以时间复杂度是 O(n)。
-
计数排序的算法思想就是这么简单,跟桶排序非常类似,只是桶的大小粒度不一样。不过,为什么这个排序算法叫“计数”排序呢?“计数”的含义来自哪里呢?
-
想弄明白这个问题,我们就要来看计数排序算法的实现方法。我还拿考生那个例子来解释。为了方便说明,我对数据规模做了简化。假设只有 8 个考生,分数在 0 到 5 分之间。这 8 个考生的成绩我们放在一个数组 A[8]中,它们分别是:2,5,3,0,2,3,0,3。
-
考生的成绩从 0 到 5 分,我们使用大小为 6 的数组 C[6]表示桶,其中下标对应分数。不过,C[6]内存储的并不是考生,而是对应的考生个数。
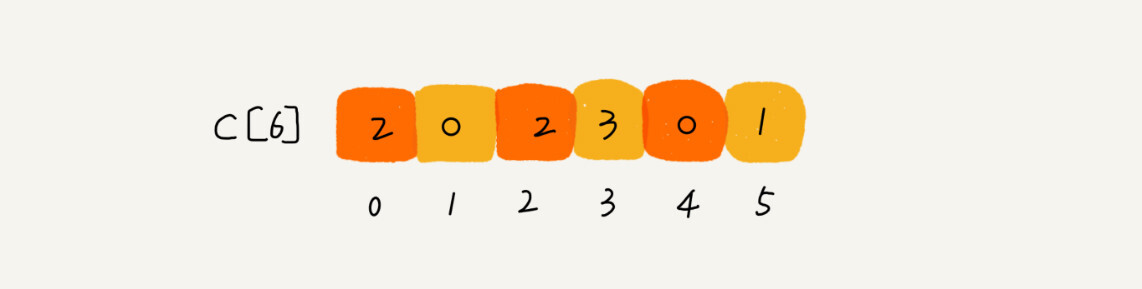
-
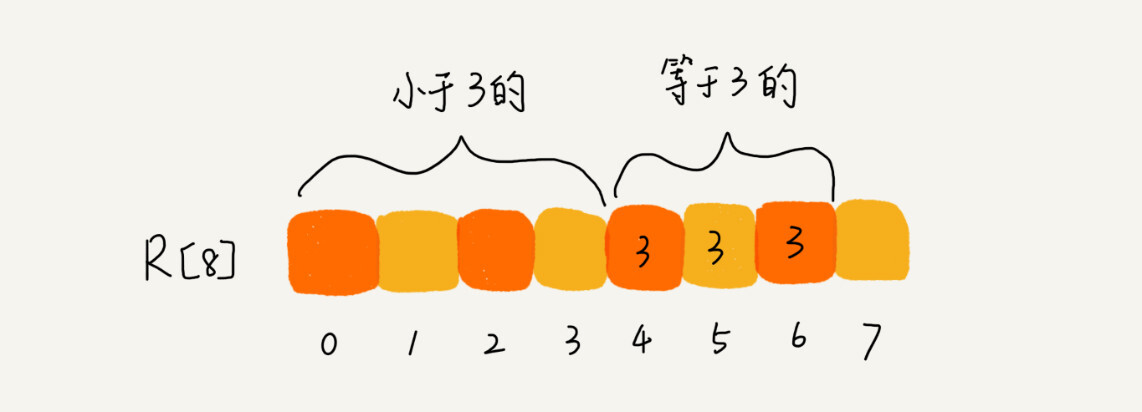
从图中可以看出,分数为 3 分的考生有 3 个,小于 3 分的考生有 4 个,所以,成绩为 3 分的考生在排序之后的有序数组 R[8]中,会保存下标 4,5,6 的位置。
-
那我们如何快速计算出,每个分数的考生在有序数组中对应的存储位置呢?
-
思路是这样的:我们对 C[6]数组顺序求和,C[6]存储的数据就变成了下面这样子。C[k]里存储小于等于分数 k 的考生个数。
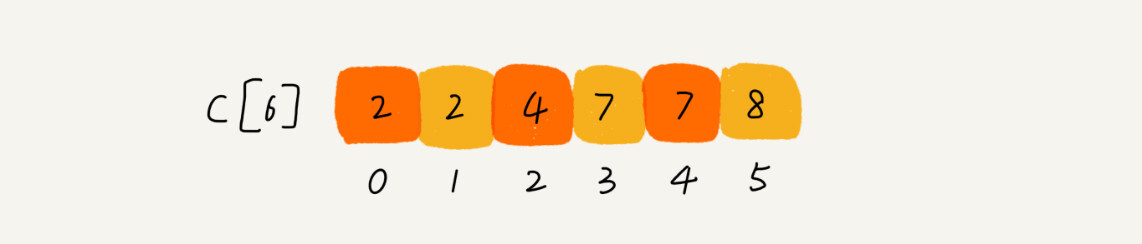
-
我们从后到前依次扫描数组 A。比如,当扫描到 3 时,我们可以从数组 C 中取出下标为 3 的值 7,也就是说,到目前为止,包括自己在内,分数小于等于 3 的考生有 7 个,也就是说 3 是数组 R 中的第 7 个元素(也就是数组 R 中下标为 6 的位置)。当 3 放入到数组 R 中后,小于等于 3 的元素就只剩下了 6 个了,所以相应的 C[3]要减 1,变成 6。
-
以此类推,当我们扫描到第 2 个分数为 3 的考生的时候,就会把它放入数组 R 中的第 6 个元素的位置(也就是下标为 5 的位置)。当我们扫描完整个数组 A 后,数组 R 内的数据就是按照分数从小到大有序排列的了。
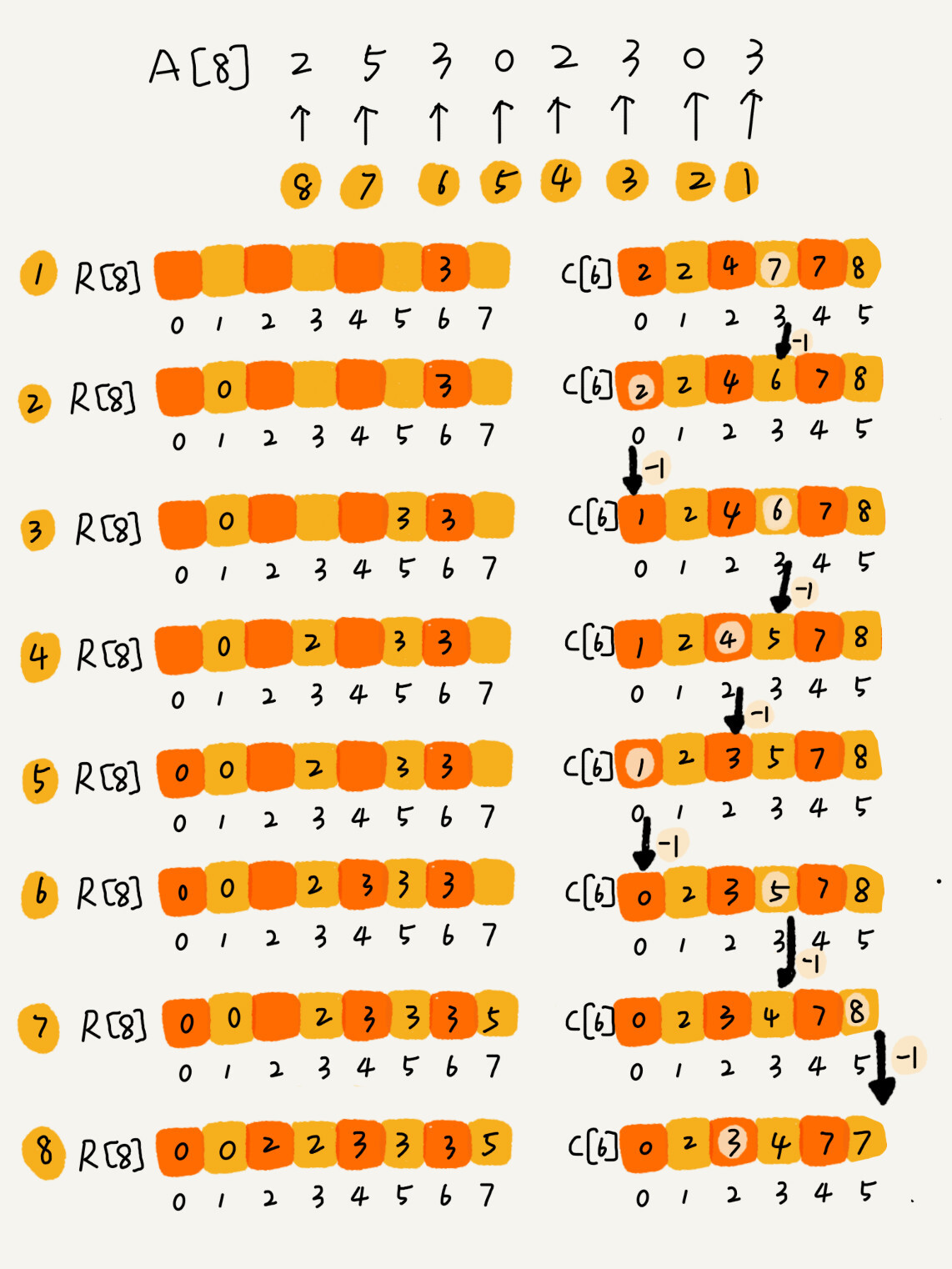
-
-
代码如下
private void CountSorting(int[] arr,int segment) { int[] bucket = new int[segment+1]; //放入桶 for (int i = 0; i < arr.Length; i++) { bucket[arr[i]]++; } int[] count = new int[bucket.Length]; int sum = 0; //计算每个桶所在的和 for (int i = 0; i < bucket.Length; i++) { sum += bucket[i]; count[i] = sum; } for (int i = bucket.Length - 1; i >= 0 ; i--) { for (int j = 0; j < bucket[i]; j++) { arr[count[i] - 1] = i; count[i]--; } } } -
计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据 n 大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
-
如何根据年龄给 100 万用户排序?
实际上,根据年龄给 100 万用户排序,就类似按照成绩给 50 万考生排序。我们假设年龄的范围最小 1 岁,最大不超过 120 岁。我们可以遍历这 100 万用户,根据年龄将其划分到这 120 个桶里,然后依次顺序遍历这 120 个桶中的元素。这样就得到了按照年龄排序的 100 万用户数据。
-
假设我们现在需要对 D,a,F,B,c,A,z 这个字符串进行排序,要求将其中所有小写字母都排在大写字母的前面,但小写字母内部和大写字母内部不要求有序。比如经过排序之后为 a,c,z,D,F,B,A,这个如何来实现呢?如果字符串中存储的不仅有大小写字母,还有数字。要将小写字母的放到前面,大写字母放在最后,数字放在中间,不用排序算法,又该怎么解决呢?
- 解:第一个两个桶,放进去拿出来就分开了
- 解第二个:三个桶
-
-
-
-
我们再来看这样一个排序问题。假设我们有 10 万个手机号码,希望将这 10 万个手机号码从小到大排序,你有什么比较快速的排序方法呢?
-
我们之前讲的快排,时间复杂度可以做到 O(nlogn),还有更高效的排序算法吗?桶排序、计数排序能派上用场吗?手机号码有 11 位,范围太大,显然不适合用这两种排序算法。针对这个排序问题,有没有时间复杂度是 O(n) 的算法呢?现在我就来介绍一种新的排序算法,基数排序。
-
借助稳定排序算法,这里有一个巧妙的实现思路。先按照最后一位来排序手机号码,然后,再按照倒数第二位重新排序,以此类推,最后按照第一位重新排序。经过 11 次排序之后,手机号码就都有序了。
-
手机号码稍微有点长,画图比较不容易看清楚,我用字符串排序的例子,画了一张基数排序的过程分解图,你可以看下。
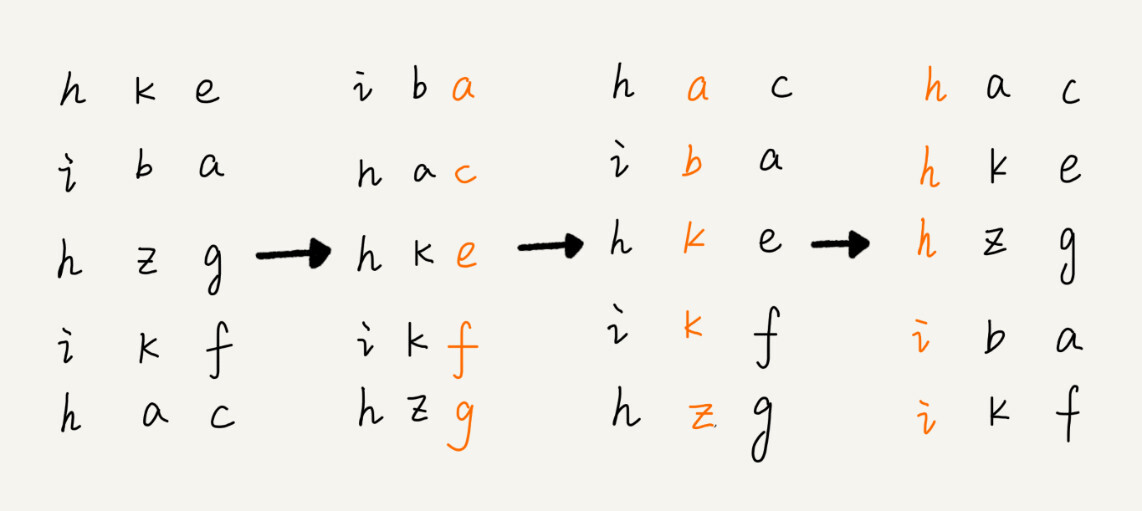
-
这里按照每位来排序的排序算法要是稳定的,否则这个实现思路就是不正确的。因为如果是非稳定排序算法,那最后一次排序只会考虑最高位的大小顺序,完全不管其他位的大小关系,那么低位的排序就完全没有意义了。
-
根据每一位来排序,我们可以用刚讲过的桶排序或者计数排序,它们的时间复杂度可以做到 O(n)。如果要排序的数据有 k 位,那我们就需要 k 次桶排序或者计数排序,总的时间复杂度是 O(k*n)。当 k 不大的时候,比如手机号码排序的例子,k 最大就是 11,所以基数排序的时间复杂度就近似于 O(n)。
-
基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系,如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到 O(n) 了。
-
-
-
如何选择合适的排序算法
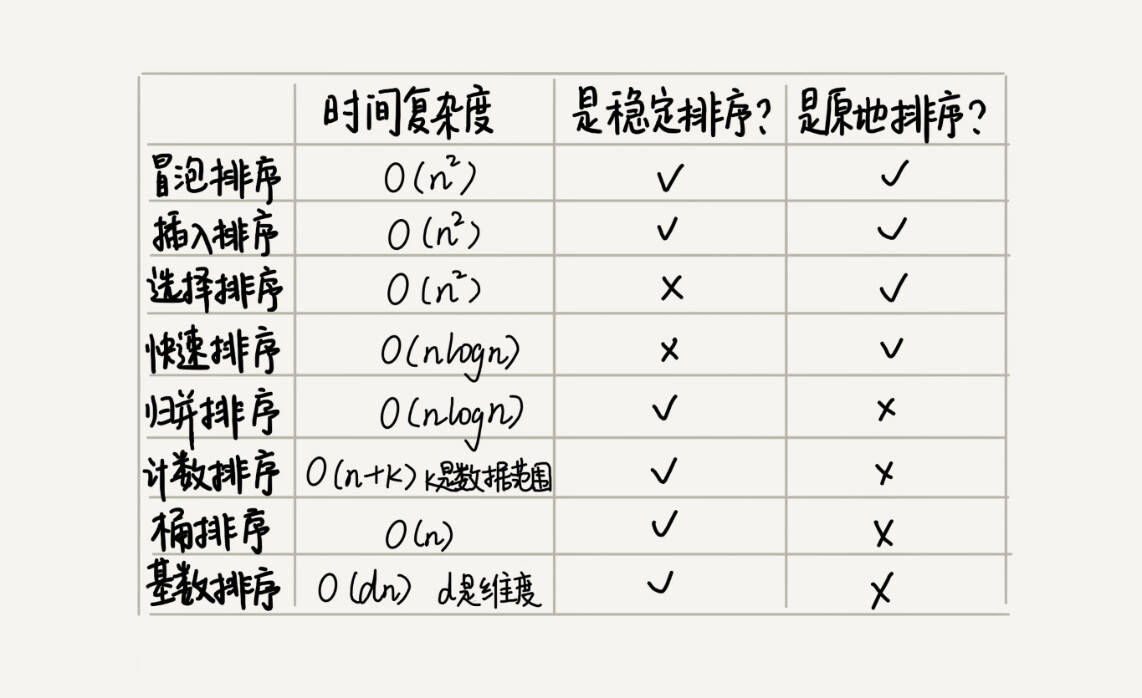
- 如果对小规模数据进行排序,可以选择时间复杂度是 O(n2) 的算法;如果对大规模数据进行排序,时间复杂度是 O(nlogn) 的算法更加高效。所以,为了兼顾任意规模数据的排序,一般都会首选时间复杂度是 O(nlogn) 的排序算法来实现排序函数。
- 时间复杂度是 O(nlogn) 的排序算法不止一个,我们已经讲过的有归并排序、快速排序,后面讲堆的时候我们还会讲到堆排序。
- 归并排序并不是原地排序算法,空间复杂度是 O(n)。所以,粗略点、夸张点讲,如果要排序 100MB 的数据,除了数据本身占用的内存之外,排序算法还要额外再占用 100MB 的内存空间,空间耗费就翻倍了。
- 快速排序比较适合来实现排序函数,但是,我们也知道,快速排序在最坏情况下的时间复杂度是 O(n2),如何来解决这个“复杂度恶化”的问题呢?
-
如何优化快速排序?
-
为什么最坏情况下快速排序的时间复杂度是 O(n^2) 呢?我们前面讲过,如果数据原来就是有序的或者接近有序的,每次分区点都选择最后一个数据,那快速排序算法就会变得非常糟糕,时间复杂度就会退化为 O(n^2)。实际上,这种 O(n^2) 时间复杂度出现的主要原因还是因为我们分区点选得不够合理。
-
那什么样的分区点是好的分区点呢?或者说如何来选择分区点呢?最理想的分区点是:被分区点分开的两个分区中,数据的数量差不多。
-
两个比较常用、比较简单的分区算法
-
三数取中法
我们从区间的首、尾、中间,分别取出一个数,然后对比大小,取这 3 个数的中间值作为分区点。这样每间隔某个固定的长度,取数据出来比较,将中间值作为分区点的分区算法,肯定要比单纯取某一个数据更好。但是,如果要排序的数组比较大,那“三数取中”可能就不够了,可能要“五数取中”或者“十数取中”。
-
随机法
随机法就是每次从要排序的区间中,随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好,但是从概率的角度来看,也不大可能会出现每次分区点都选得很差的情况,所以平均情况下,这样选的分区点是比较好的。时间复杂度退化为最糟糕的 O(n2) 的情况,出现的可能性不大。
-
-
快速排序是用递归来实现的,递归要警惕堆栈溢出。为了避免快速排序里,递归过深而堆栈过小,导致堆栈溢出,我们有两种解决办法
- 限制递归深度。一旦递归过深,超过了我们事先设定的阈值,就停止递归。
- 通过在堆上模拟实现一个函数调用栈,手动模拟递归压栈、出栈的过程,这样就没有了系统栈大小的限制。
-
-
举例分析排序函数
- Glibc 中的 qsort()
- qsort() 会优先使用归并排序来排序输入数据,因为归并排序的空间复杂度是 O(n),所以对于小数据量的排序,比如 1KB、2KB 等,归并排序额外需要 1KB、2KB 的内存空间,这个问题不大。现在计算机的内存都挺大的,我们很多时候追求的是速度。还记得我们前面讲过的用空间换时间的技巧吗?这就是一个典型的应用。
- 要排序的数据量比较大的时候,qsort() 会改为用快速排序算法来排序。qsort() 选择分区点的方法就是“三数取中法”,对于递归太深会导致堆栈溢出的问题,qsort() 是通过自己实现一个堆上的栈,手动模拟递归来解决的。
- 实际上,qsort() 并不仅仅用到了归并排序和快速排序,它还用到了插入排序。在快速排序的过程中,当要排序的区间中,元素的个数小于等于 4 时,qsort() 就退化为插入排序,不再继续用递归来做快速排序,因为我们前面也讲过,在小规模数据面前,O(n^2) 时间复杂度的算法并不一定比 O(nlogn) 的算法执行时间长。我们现在就来分析下这个说法。
- 时间复杂度代表的是一个增长趋势,如果画成增长曲线图,你会发现 O(n2) 比 O(nlogn) 要陡峭,也就是说增长趋势要更猛一些。但是,我们前面讲过,在大 O 复杂度表示法中,我们会省略低阶、系数和常数,也就是说,O(nlogn) 在没有省略低阶、系数、常数之前可能是 O(knlogn + c),而且 k 和 c 有可能还是一个比较大的数。
- 假设 k=1000,c=200,当我们对小规模数据(比如 n=100)排序时,n2的值实际上比 knlogn+c 还要小。
- Glibc 中的 qsort()
-
查找
-
-
原理
-
二分查找是一种非常简单易懂的快速查找算法,生活中到处可见。比如说,我们现在来做一个猜字游戏。我随机写一个 0 到 99 之间的数字,然后你来猜我写的是什么。猜的过程中,你每猜一次,我就会告诉你猜的大了还是小了,直到猜中为止。你来想想,如何快速猜中我写的数字呢?假设我写的数字是 23,你可以按照下面的步骤来试一试。(如果猜测范围的数字有偶数个,中间数有两个,就选择较小的那个。)
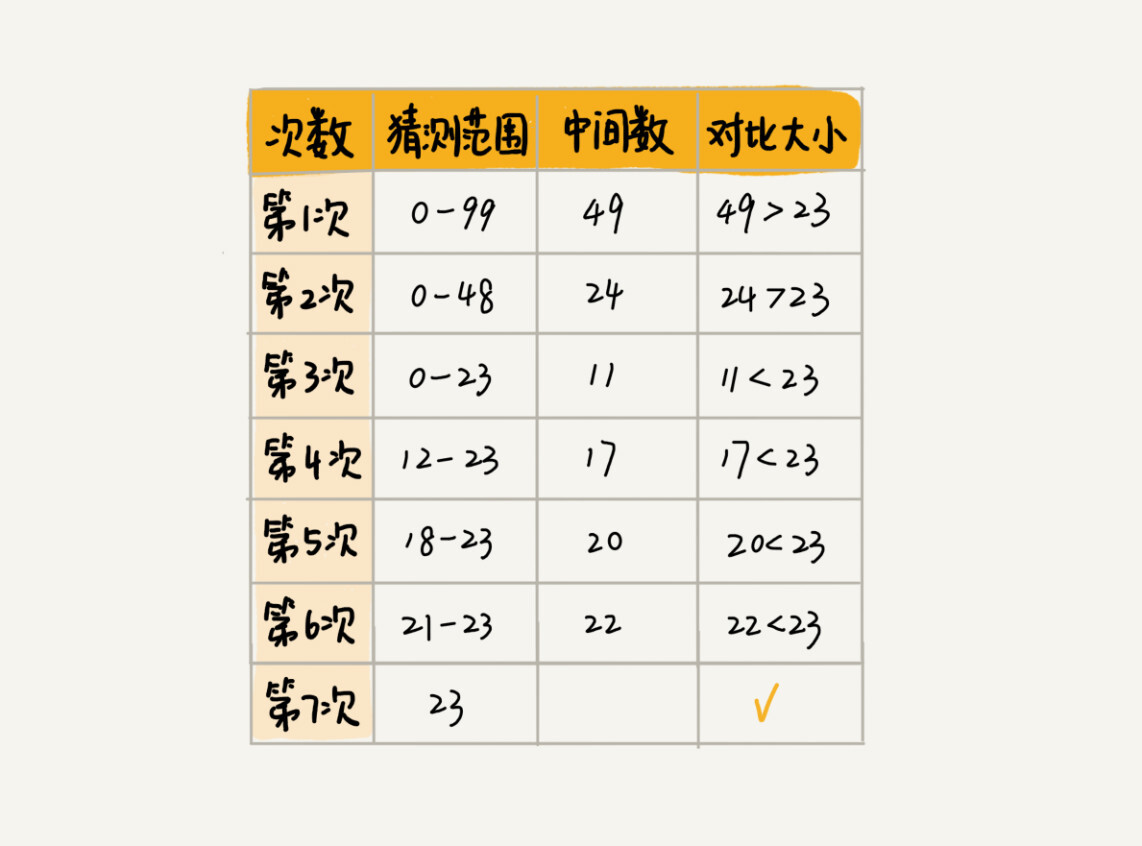
-
7 次就猜出来了,是不是很快?这个例子用的就是二分思想,按照这个思想,即便我让你猜的是 0 到 999 的数字,最多也只要 10 次就能猜中。
-
利用二分思想,每次都与区间的中间数据比对大小,缩小查找区间的范围。为了更加直观,我画了一张查找过程的图。其中,low 和 high 表示待查找区间的下标,mid 表示待查找区间的中间元素下标。
-
二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
-
-
O(logn) 惊人的查找速度
- 二分查找是我们目前为止遇到的第一个时间复杂度为 O(logn) 的算法。后面章节我们还会讲堆、二叉树的操作等等,它们的时间复杂度也是 O(logn)。我这里就再深入地讲讲 O(logn) 这种对数时间复杂度。这是一种极其高效的时间复杂度,有的时候甚至比时间复杂度是常量级 O(1) 的算法还要高效。为什么这么说呢?
- 因为 logn 是一个非常“恐怖”的数量级,即便 n 非常非常大,对应的 logn 也很小。比如 n 等于 2 的 32 次方,这个数很大了吧?大约是 42 亿。也就是说,如果我们在 42 亿个数据中用二分查找一个数据,最多需要比较 32 次。
- 我们前面讲过,用大 O 标记法表示时间复杂度的时候,会省略掉常数、系数和低阶。对于常量级时间复杂度的算法来说,O(1) 有可能表示的是一个非常大的常量值,比如 O(1000)、O(10000)。所以,常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。
-
基本二分查找的递归与非递归实现
-
递归版本
private int BinarySearch(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if (arr[mid] == findValue) return mid; else if (arr[mid] > findValue) return BinarySearch(arr, low, mid - 1, findValue); else return BinarySearch(arr, mid + 1, high , findValue); } -
非递归版
private int BinarySearch(int[] arr,int findValue) { int low = 0; int high = arr.Length-1; int mid = 0; do { mid = low + (high - low) / 2; if (arr[mid] == findValue) return mid; else if (arr[mid] > findValue) high = mid - 1; else low = mid + 1; } while (low <= high); return -1; } -
坑点
-
循环退出条件
-
mid 的取值
实际上,mid=(low+high)/2 这种写法是有问题的。因为如果 low 和 high 比较大的话,两者之和就有可能会溢出。改进的方法是将 mid 的计算方式写成 low+(high-low)/2。更进一步,如果要将性能优化到极致的话,我们可以将这里的除以 2 操作转化成位运算 low+((high-low)>>1)。因为相比除法运算来说,计算机处理位运算要快得多。
-
low 和 high 的更新
low=mid+1,high=mid-1。注意这里的 +1 和 -1,如果直接写成 low=mid 或者 high=mid,就可能会发生死循环。比如,当 high=3,low=3 时,如果 a[3]不等于 value,就会导致一直循环不退出。
-
-
二分查找应用场景的局限性
-
二分查找的时间复杂度是 O(logn),查找数据的效率非常高。不过,并不是什么情况下都可以用二分查找,它的应用场景是有很大局限性的。那什么情况下适合用二分查找,什么情况下不适合呢?
-
首先,二分查找依赖的是顺序表结构,简单点说就是数组或者其他支持随机访问的数据结构。
那二分查找能否依赖其他数据结构呢?比如链表。答案是不可以的,主要原因是二分查找算法需要按照下标随机访问元素。我们在数组和链表那两节讲过,数组按照下标随机访问数据的时间复杂度是 O(1),而链表随机访问的时间复杂度是 O(n)。所以,如果数据使用链表存储,二分查找的时间复杂就会变得很高。
-
二分查找针对的是有序数据
-
数据量太小不适合二分查找。
果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素,不管用二分查找还是顺序遍历,查找速度都差不多。只有数据量比较大的时候,二分查找的优势才会比较明显。
不过,这里有一个例外。如果数据之间的比较操作非常耗时,不管数据量大小,我都推荐使用二分查找。比如,数组中存储的都是长度超过 300 的字符串,如此长的两个字符串之间比对大小,就会非常耗时。我们需要尽可能地减少比较次数,而比较次数的减少会大大提高性能,这个时候二分查找就比顺序遍历更有优势。
-
数据量太大也不适合二分查找。
二分查找的底层需要依赖数组这种数据结构,而数组为了支持随机访问的特性,要求内存空间连续,对内存的要求比较苛刻。比如,我们有 1GB 大小的数据,如果希望用数组来存储,那就需要 1GB 的连续内存空间。
-
-
-
如何在内存限制为内存限制是100MB的情况下从1000 万个整数中快速查找某个整数?
- 我们的内存限制是 100MB,每个数据大小是 8 字节,最简单的办法就是将数据存储在数组中,内存占用差不多是 80MB,符合内存的限制。借助今天讲的内容,我们可以先对这 1000 万数据从小到大排序,然后再利用二分查找算法,就可以快速地查找想要的数据了。
- 看起来这个问题并不难,很轻松就能解决。实际上,它暗藏了“玄机”。如果你对数据结构和算法有一定了解,知道散列表、二叉树这些支持快速查找的动态数据结构。你可能会觉得,用散列表和二叉树也可以解决这个问题。实际上是不行的。
- 虽然大部分情况下,用二分查找可以解决的问题,用散列表、二叉树都可以解决。但是,我们后面会讲,不管是散列表还是二叉树,都会需要比较多的额外的内存空间。如果用散列表或者二叉树来存储这 1000 万的数据,用 100MB 的内存肯定是存不下的。而二分查找底层依赖的是数组,除了数据本身之外,不需要额外存储其他信息,是最省内存空间的存储方式,所以刚好能在限定的内存大小下解决这个问题。
-
-
二分查找的变体
-
一张图直接到位

-
变体一:查找第一个值等于给定值的元素
-
思路
- 如果我们查找的是任意一个值等于给定值的元素,当 a[mid]等于要查找的值时,a[mid]就是我们要找的元素。但是,如果我们求解的是第一个值等于给定值的元素,当 a[mid]等于要查找的值时,我们就需要确认一下这个 a[mid]是不是第一个值等于给定值的元素。
- 如果 mid 等于 0,那这个元素已经是数组的第一个元素,那它肯定是我们要找的;如果 mid 不等于 0,但 a[mid]的前一个元素 a[mid-1]不等于 value,那也说明 a[mid]就是我们要找的第一个值等于给定值的元素。
-
代码
private int BinarySearchFirst(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if (arr[mid] == findValue) { if (mid - 1 >= 0 && arr[mid - 1] == findValue) //当前项不是第一个 return BinarySearchFirst(arr, low, mid - 1, findValue); else return mid; } else if (arr[mid] > findValue) return BinarySearchFirst(arr, low, mid - 1, findValue); else return BinarySearchFirst(arr, mid + 1, high , findValue); }
-
-
变体二:查找最后一个值等于给定值的元素
-
思路
- 同上,就换成了检测mid+1
-
代码
private int BinarySearchLast(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if (arr[mid] == findValue) { if (mid + 1 < arr.Length && arr[mid + 1] == findValue) //当前项不是最后一个 return BinarySearchLast(arr, mid + 1, high , findValue); else return mid; } else if (arr[mid] > findValue) return BinarySearchLast(arr, low, mid - 1, findValue); else return BinarySearchLast(arr, mid + 1, high , findValue); }
-
-
变体三:查找第一个大于等于给定值的元素
-
思路
- 之前找到的是等于findVal的值,现在条件改成判断的是大于findVal切前面那个比findVal小的齐活
-
代码
private int BinarySearchFirstGreater(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if ((arr[mid] > findValue && mid == 0) || arr[mid] > findValue && (mid - 1 > 0 && arr[mid - 1] <= findValue)) return mid; else if (arr[mid] == findValue) return BinarySearchFirstGreater(arr, mid + 1, high , findValue); else if (arr[mid] < findValue) return BinarySearchFirstGreater(arr, mid + 1, high , findValue); else return BinarySearchFirstGreater(arr, low, mid - 1, findValue); }
-
-
变体四:查找最后一个小于等于给定值的元素
-
思路
- 类似上面,换个方向,送分题
-
代码
private int BinarySearchLastLess(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if ((arr[mid] < findValue && mid == arr.Length-1) || arr[mid] < findValue && (mid + 1 < arr.Length && arr[mid + 1] >= findValue)) return mid; else if (arr[mid] == findValue) return BinarySearchLastLess(arr, low, mid - 1, findValue); else if (arr[mid] > findValue) return BinarySearchLastLess(arr, low, mid - 1, findValue); else return BinarySearchLastLess(arr, mid + 1, high , findValue); }
-
-
变体的二分查找算法写起来非常烧脑,很容易因为细节处理不好而产生 Bug,这些容易出错的细节有:终止条件、区间上下界更新方法、返回值选择。
-
-
习题
-
假设我们有 12 万条这样的 IP 区间与归属地的对应关系,如何快速定位出一个 IP 地址的归属地呢?
- 12W个区间,可以理解为有24W个有序的元素。 把要查找的IP地址转化为一个整型的数字,利用二分查找去查找,最后一个小于等于这个IP整型数字的元素。 如果找了这个元素,还要比较下要查询的IP地址元素值要大于等于找到的这个元素的前面那个元素的值。这么做的目的,就是要确认一下,这个IP恰好就在我们两个数据元素的区间内,如果都满足了的话,那么就直接返回这个元素所代表的的归属地的信息。如果找不到,那么就返回-1。
-
如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?33. 搜索旋转排序数组
-
有三种方法查找循环有序数组
-
方法一
-
找到分界下标,分成两个有序数组
-
判断目标值在哪个有序数据范围内,做二分查找
-
-
方法二
- 找到最大值的下标 x
- 所有元素下标 +x 偏移,超过数组范围值的取模
- 利用偏移后的下标做二分查找
- 如果找到目标下标,再作 -x 偏移,就是目标值实际下标。
-
方法三
- 上述两种方法的时间耗费最高时耗都在查找分界点上,所以时间复杂度是 O(N)。
- 方法三用了一个很骚的操作,现在已知左侧是大的有序数,右侧是小的有序数。
- 先吧数组最后一个值和中位数比一下
- 如果小于中位数,那就知道左侧这半边全部有序,那就对左侧有序数组进行二分查找找指定值,如果找到则over
- 如果大于中位数,那就知道右侧这半边全部有序,那就对右侧有序数组进行二分查找找指定值,如果找到则over
- 找不到的话在对剩下的数组又拿最后一个和剩下数组的中位数比,重复上述操作
- 如果两边都搜完了还是没找到那就返回-1,不然肯定搜得到
- 时间复杂度为 O(logN)
public int Search(int[] nums, int target) { int last = nums[nums.Length-1]; int mid = 0; int low = 0; int high = nums.Length - 1; int find = -1; do { mid = low + (high - low) / 2; if (nums[mid] > last) { find = BinarySearch(nums, low, mid, target); low = mid + 1; } else { find = BinarySearch(nums, mid, high, target); high = mid - 1; } if (find != -1) return find; } while (low <= high); return find; } private int BinarySearch(int[] arr,int low,int high,int findValue) { if (low > high) return -1; int mid = low + (high - low) / 2; if (arr[mid] == findValue) return mid; else if (arr[mid] > findValue) return BinarySearch(arr, low, mid - 1, findValue); else return BinarySearch(arr, mid + 1, high , findValue); }
-
-
-
-


