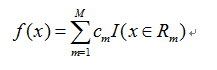Boosting算法之Adaboost和GBDT
Boosting是串行式集成学习方法的代表，它使用加法模型和前向分步算法，将弱学习器提升为强学习器。Boosting系列算法里最著名的算法主要有AdaBoost和梯度提升系列算法(Gradient Boost，GB)，梯度提升系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Decision Tree，GBDT)。
一、Adaboost
1、Adaboost介绍
Adaboost算法通过在训练集上不断调整样本权重分布，基于不同的样本权重分布，重复训练多个弱分类器，最后通过结合策略将所有的弱分类器组合起来，构成强分类器。Adaboost算法在训练过程中，注重减少每个弱学习器的误差，在训练下一个弱学习器时，根据上一次的训练结果，调整样本的权重分布，更加关注那些被分错的样本，使它们在下一次训练中得到更多的关注，有更大的可能被分类正确。
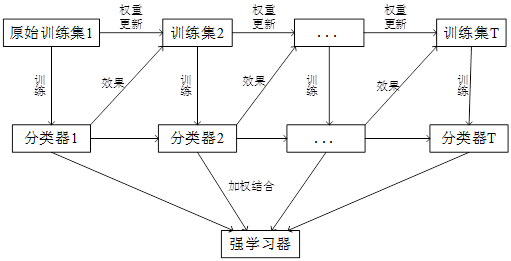
Adaboost算法框架图
2、Adaboost算法过程
1)初始化样本权重，一共有n个样本，则每个样本的权重为1/n
2)在样本分布Dt上，训练弱分类器，for t=1,2，……T：
a、训练分类器ht
b、计算当前弱分类器的分类误差率
c、判断误差率是否小于0.5，是则继续，否则退出循环
d、计算当前弱分类器的权重系数alpha值
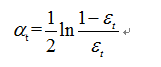
e、根据alpha值调整样本分布Dt+1
如果样本被正确分类，则该样本的权重更改为：
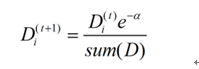
如果样本被错误分类，则该样本的权重更改为：
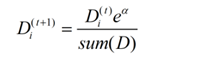
3)组合弱分类器得到强分类器
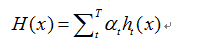
3、算法伪代码：
AdaBoost算法每一轮都要判断当前基学习器是否满足条件，一旦条件不满足，则当前学习器被抛弃，且学习过程停止。Adaboost算法使用指数损失函数，通过最小化指数损失函数，得到在每次迭代中更新的权重参数计算公式。AdaBoost算法使用串行生成的序列化方法，多个基学习器之间存在强依赖关系。Adaboost的每一个弱分类器的目标，都是为了最小化损失函数，下一个弱分类器是在上一个分类器的基础上对错分样本进行修正，所以， AdaBoost算法是注重减小偏差的算法。
Adaboost提供的是一种框架，可使用任何分类器作为基学习器，适用很多分类场景，通常可以获得不错的分类效果，例如，基于Adaboost的人脸检测算法。
二、GBDT
1、GBDT介绍
GBDT在竞赛和工业中都经常使用，能有效的应用于分类，回归，排序问题，通常能有不错的效果，是一种应用非常广泛的算法。GBDT是梯度提升算法，也是采用加法模型。GBDT以CART回归树作为基学习器，通过迭代，每次通过拟合负梯度来构建新的CART回归树，通过构建多颗CART树来降低模型的偏差，实现更好的分类性能。GBDT的核心思想是在每次创建新的CART回归树时，通过拟合当前模型损失函数的负梯度，来最小化损失函数。GBDT用于分类和回归时都使用CART回归树，分类时使用指数损失或对数损失，回归时使用平方误差损失函数，绝对值损失函数，Huber损失函数等。当GBDT使用平方误差作为损失函数时，负梯度正好是残差。
GBDT用CART回归树为基分类器，在每次构建新树时，将样本在当前模型的残差作为样本标签来训练下一颗树，经过多次迭代提升模型的分类性能。决策树和GBDT虽然结果相同，但是决策树容易过拟合，泛化能力差，可能在当前训练集上表现较好，在其他数据集上效果较差，而GBDT是结合了多颗树模型，具有较好的泛化能力。
2、GBDT回归算法
GBDT算法过程就是创建多颗CART回归树的过程，只是在创建下一颗树的时候拟合当前模型的负梯度，就是将样本在当前模型的负梯度作为标签，去构建下一颗树。GBDT用于分类时也使用CART回归树，输出类别值，不能直接拟合负梯度，这里只介绍GBDT回归算法。
输入：训练集D={(x1,y1),(x2,y2),……,(xm,ym)}，最大迭代次数T，损失函数L
输出：强学习器f(X)
1) 初始化弱学习器
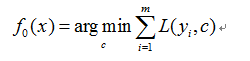
2) 对迭代次数t=1,2,……,T有：
a.对样本i=1,2,……,m，计算负梯度
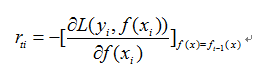
b.利用(xi,rti)，拟合一颗CART回归树，得到第t可回归树，其对应的叶子节点区域为Rtj，J=1,2，……，J。其中J表示回归树t的叶子节点的个数。
c.对叶子区域j=1,2,……,J,计算最佳拟合值
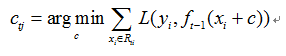
d．更新强学习器
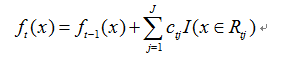
3) 得到强学习器表达式
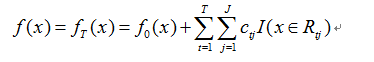
3、GBDT算法负梯度拟合
GBDT是加法模型，当前模型可表示为
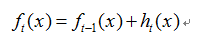
其中，是第m颗树。
当前损失函数为
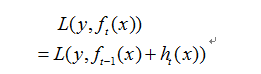
泰勒一阶展开公式为：
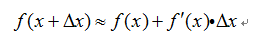
对当前损失函数泰勒一阶展开
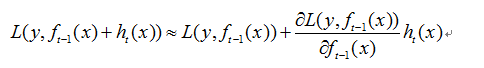
梯度下降公式
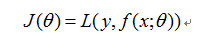
其中，表示损失函数，是关于参数的式子
在梯度方向损失函数减少最快，最小化损失函数，用梯度下降法求解参数
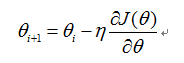
同理，最小化损失函数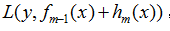
，用梯度下降法求解，则
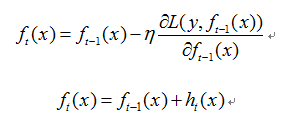
故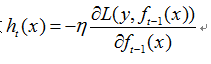
所以GBDT算法每次迭代创建新的CART树ht(x)，实质上是在拟合损失函数的负梯度，利用梯度下降算法在函数空间求解。当GBDT使用均方误差作为损失函数时，此时的负梯度正好是残差。
GBDT的优点：
（1）可用于所有回归问题（包括线性和非线性问题）
（2）可构造组合特征，通常用GBDT构造的组合特征加上原来的特征一起输入LR模型做分类
（3）可得到特征的重要权重值
GBDT的正则化有三种方式：
（1）子采样
（2）步长
（3）CART树剪枝
4、CART回归树
CART假设决策树是二叉树，递归地二分每个特征，将输入空间划分为有限个单元，并在这些单元上确定预测的概率分别，也就是在输入给定的条件下输出的条件概率分布。
CART算法由两步组成：
（1）决策树生成
（2）决策树剪枝
CART回归树的建树过程和其他决策树一样，同样是寻找最优划分特征和最优切分点。
CART回归树用平方误差最小化划分节点
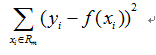
当输入空间的划分确定时，用平方误差来表示回归树对于训练数据的预测误差，用平方误差最小的准则求解每个单元上的最优输出值。所以，单元Rm上的cm的最优值是Rm上的所有输入实例xi对应的输出yi的均值，在一个划分单元Rm上的样本的取值相同。
故单元Rm的值cm是
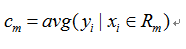
回归树生成过程：
（1）寻找最优切分变量和最优切分点，遍历所有特征j的所有划分点s，求解
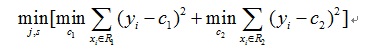
c1、c2是左右两个节点上的实例的y的平均值。
（2）用选定的(j,s)对划分区域并计算相应的输出值：
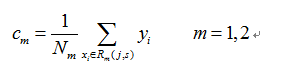
（3）继续对两个子区域调用步骤（1），（2），直至满足停止条件。
（4）将输入空间划分为M个区域R1，R2，……，RM，生成决策树：
