offline RL · PbRL | Preference Transformer：反正感觉 transformer 很强大


内容总结

  • （为什么感觉挺 A+B 的，有点想不明白为何会中…… 不过 writing 貌似很好）
  • 提出了新的 preference model，σ0＞σ1 的概率仍然是 exp[Σ reward_0] / (exp[Σ r0] + exp[Σ r1]) 的形式，但 exp[] 里面的内容从 reward 求和（discounted reward 求和）变成 Σ r · w，其中 w 是一个 importance weight。
  • 这里的 motivation：
    • ① human preference 可能基于 non-Markovian reward，因此用 transformer 建模 trajectory，作为 reward model 的一部分；
    • ② human 可能会关注关键帧，因此需要一个 importance weight，为先前提到的 non-Markovian reward 加权。
  • 然后，利用 attention layer 的 key query value 形式，将 value 作为 reward，softmax(key · query) 作为 importance weight。（正好跟 attention 的形式 match 上）

技术路线：

  • 学 reward model → 对 offline trajectory 标记 reward → offline RL。
  • 学习 reward · importance weight 的 model，使用 transformer 来训，其中输入是 s a s a 的 trajectory，每个当前 trajectory 都会输出一个 reward · importance weight，然后把它们加权求和 去做 preference 的 loss。
  • 然后对 offline dataset 进行 reward label 和 IQL。

0 abstract

Preference-based reinforcement learning (RL) provides a framework to train agents using human preferences between two behaviors. However, preference-based RL has been challenging to scale since it requires a large amount of human feedback to learn a reward function aligned with human intent. In this paper, we present Preference Transformer, a neural architecture that models human preferences using transformers. Unlike prior approaches assuming human judgment is based on the Markovian rewards which contribute to the decision equally, we introduce a new preference model based on the weighted sum of non-Markovian rewards. We then design the proposed preference model using a transformer architecture that stacks causal and bidirectional self-attention layers. We demonstrate that Preference Transformer can solve a variety of control tasks using real human preferences, while prior approaches fail to work. We also show that Preference Transformer can induce a well-specified reward and attend to critical events in the trajectory by automatically capturing the temporal dependencies in human decision-making.

  • background：
    • PbRL 框架用于在两种行为之间使用 human preference 来训练 agent。然而，需要大量 human feedback，来学习与人类意图一致的 reward model。
  • method：
    • 在本文中，我们介绍了 preference transformer，使用 transformer 架构模拟 human preference。
    • 以前方法假设，人类判断基于 Markovian reward，而 Markovian reward 对决策的贡献相同。与先前工作不同，我们引入了一种 preference model，该模型基于 non-Markovian reward 的加权和。
    • 然后，我们在 preference model 的 transformer 设计里，堆叠 causal self-attention layers 和 bidrectional self-attention layers。
  • results：
    • Preference Transformer 可以使用真实 human feedback 来解决各种控制任务，而以前的方法无法奏效。
    • Preference Transformer 可以通过自动捕获人类决策中的时间依赖性（temporal dependencies），来得到一个 well-specified reward 并关注轨迹中的关键事件。

open review 与项目网站

  • open review：
    • 主要贡献：① 提出了一个基于 non-Markovian reward 加权和的新 preference model，② 引入 PT 来模拟所提出的 preference model。
    • 如果奖励实际上是 non-Markovian 的，那么 Transformer 的想法是有动机的（well motivated）。
    • The paper is well written. 论文写得很好。
    • scripted evaluation（大概是 scripted teacher）使用 Markovian reward，但 NMR（non-Markovian reward）和 PT 仍能在多个领域优于 MR（Markovian reward）变体。这需要得到更好的解释和评估。事实上，应该使用 non-Markovian reward 进行评估。
  • 项目网站：
    • Preference Transformer 将 trajectory segment 作为输入，从而提取与任务相关的历史信息。
    • 通过堆叠 bidirectional 和 causal self-attention layers，Preference Transformer 生成 non-Markovian reward 和重要性权重（importance weights）作为输出。（貌似 importance weight 越高，某帧在整个 trajectory 里越重要）
    • 我们利用它们来定义 preference model，并发现 PT 可以得到 better-shaped reward，并从 human preference 中关注关键事件。
    • 实验证明，PT 可用于学习复杂的新行为（Hopper 多次后空翻），这很难设计合适的奖励函数。与单个后空翻相比，这项任务更具挑战性，因为奖励函数必须捕获 non-Markovian 上下文，包括旋转次数（有必要嘛？）。观察到，PT agent 在稳定着陆的情况下执行多个后空翻，而基于 MLP 的 Markovian reward 的 agent 很难着陆。

1 基于 non-Markovian reward 的 preference model

  • motivation：
    • 首先，在许多情况下，很难使用 Markovian reward 来给出任务的描述。
    • 此外，由于人类对于非凡的时刻很敏感，因此可能需要在轨迹内分配 credit（大概是权重的意思）。
  • non-Markovian reward function：
    • reward function 的输入：先前的完整的 sub-trajectory。
    • 同时再整一个权重函数 w = w({s, a, s, ...})，其输入也是 t 时刻之前的完整 sub-trajectory。
    • 用 r(τ) · w(τ) 来改写 \(P(\sigma^1\succ\sigma^0)=\bigg[\exp\big(\sum_tr(\tau_t)\cdot w(\tau_t)\big)\bigg]/\bigg[\exp(\sum r\cdot w)_{\sigma^0}+\exp(\sum r\cdot w)_{\sigma^1} \bigg]\) 的公式。

2 PT 的架构

  • 感觉 causal transformer 相对好理解，以及 GPT 具有 causally masked self-attention。
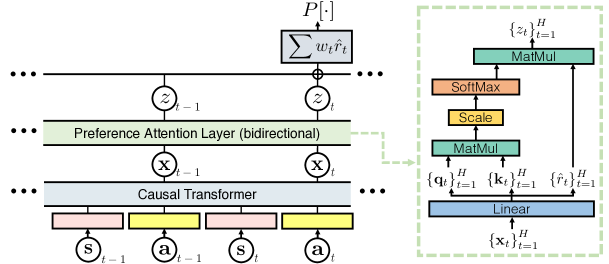
  • preference attention layer：
    • causal transformer 生成的 {x, x, ...} sequence，过一个线性层，会得到它们的 key query value。
    • 认为得到的这个 value 就是 reward，而 key 与 query 相乘再 softmax（保证＞0）则是权重。
  • 好像这只是一个 reward model，而非 RL policy（？）
    • 学到 reward model 后，还需要使用 IQL 学 policy…
Refer to caption

3 PT 的训练与 inference

  • training：最小化 cross-entropy loss \(L=-\mathbb E[(1-y)\log P[\sigma^0\succ\sigma^1]+y\log P[\sigma^1\succ\sigma^0]]\) ，其中 y 是 label，P 是我们训练的概率。
  • inference：如何得出 agent 的 reward。
    • 好像是直接拿 reward（而非 reward · importance weight）来做。
    • 大致流程：拿 st, at, s, ... 送进 causal transformer，然后得到 xt, ...，送进 preference attention layer，得到 r hat，单独取出 r hat。

4 experiments

关注的问题：

  • Preference Transformer 能否使用真实的人类偏好解决复杂的控制任务？
  • PT 能否 induce 一致（consistent）的 reward 并关注关键事件？
  • PT 在合成偏好（synthetic preferences，即 scripted teacher setting）中的表现如何？

baseline：

  • 技术路线：preference → reward model → IQL。
  • 1 通过 preference loss 的形式，学习 MLP 的 Markovian reward，输入 s a 输出 reward。
  • 2 通过 preference loss 的形式，基于 LSTM 的 non-Markovian reward，输入 s a s a，输出 reward。

results：

  • PT 在几乎所有任务中，都始终优于所有 baselines。特别的，只有 PT 几乎将 IQL 的性能与使用 ground-truth reward 相匹配，而 baselines 在困难的任务中基本不 work。
  • 让 PT 和 Markovian 或 LSTM agent 分别生成 trajectory，让 human 评价哪个更好，human 评价 PT 更好。
  • 在所谓的“PT 是否可以诱导（induce）一个明确（well-specified）的奖励”这一段，好像也只是感性分析了一下…
  • 在比较 scripted teacher 和 human 时，因为 scripted teacher 不能理解 contex，所以 human preference 反而在简单任务上表现更好；并且，它们的 preference 会在简单的 grid-world 中发生分歧。
  • 学习复杂的新行为：很炫酷的 hopper 空中多个后空翻的 demo。

5 好像很有道理的 future work

  • 在 RL 或 PbRL 中利用重要性权重，或许可以用于对信息量更大的 query / samples 进行采样，这可以提高 sample-efficiency。
  • 使用重要性权重，通过加权更新，来稳定 Q 学习。
  • 与其他偏好模型结合：例如 Knox et al.（2022）的基于 regret 的 preference model（title: Models of human preference for learning reward functions），尽管他们提出的方法基于几个假设（例如，生成后续特征（Dayan，1993;Barreto et al.， 2017）），与基于遗憾的模型相结合会很有趣。（这个暂时没看懂如何做）


posted @ 2024-03-06 12:57  MoonOut  阅读(90)  评论(1)  编辑  收藏  举报