凸优化 | 期末复习笔记存档

这是自动化系的凸优化期末复习笔记，应该覆盖所有考点了。据可靠情报，至少 2023 秋季学期，两位老师的考题是一样的。

想起来，考试时考察凸集，有问到一个腐蚀球的问题；大概先定义了腐蚀（若 r=1 的球被凸集包含，则球心在腐蚀后的凸集里）。去证明凸集腐蚀后还是凸的（或者类似的证明）。
证明思路：若 a b 都在腐蚀集内，则 c=θa+(1-θ)b 也在腐蚀集内，对于 c 球内任意一个点，都可以在 a 球 b 球内找到对应的点，然后线性组合；这一步线性组合是可以做的，因为腐蚀前的集合是凸集；这样就得到了。（这个题考试时没想到做法，乱糊了一个……

（记下来，以防之后忘记又回想……）

---

目录

• 考察范围
  • 课本框架
  • 课堂情报
  • 往年题目情报
• 1 凸集
• 2 凸函数
• 3 凸优化问题
• 4 对偶问题 & KKT 条件
• 5 搜索算法
  • 第 9 章 - 无约束优化：
  • 第 10 章 - 等式约束优化：
  • 第 11 章 - 不等式约束优化：

---

考察范围

课本框架

• 2 凸集定义，3 凸函数 保凸运算（拟凸 不会考）。
• 4 凸优化问题。
• 5 对偶。
• 9 无约束优化 10 等式约束优化 11 障碍函数 内点法，不考复杂性分析，考算法模拟。

课堂情报

• 保凸运算，拟凸 不会考
• 凸优化问题：除了向量优化不考，其他都考。
  • 定义，线性 二次 QCQP SOCP SEP 锥规划，几何规划 geometric 正定规划（？）
• 对偶 5.1 - 5.6，拉格朗日函数 对偶问题，不同的解释（几何解释 鞍点解释），KKT 最优性条件。
  • 不考 friz john，slater 条件需要记，扰动条件可能考，影子价格
• 应用不考
• （第九章？）复杂度分析（收敛多快）不考，不会现场编程，跟作业差不多，迭代一部两步，手动算一下，带计算器。
• 10.1 - 10.3 等式约束，各种不同的牛顿法。
• 11.4 什么可行性阶段性方法，11.7 原对偶问题。

往年题目情报

• 凸集：
  • 判断是否凸集。
  • 凸集分离定理。
• 凸函数：
  • 判断是否凸函数。
• 凸规划问题：
  • 转化为凸优化问题，写成 xxx 的形式，给出最优解和最优值。
  • 是否是凸优化问题，是否满足强对偶性，是否有 K-T 解（？）
• 对偶：
  • 写出对偶问题和 KKT 条件，求原问题 对偶问题最优解，检测是否满足强对偶性。
• 搜索：
  • 考虑二次规划问题 xxx，用对数障碍函数处理不等式约束，用梯度下降法求解。

1 凸集

• 凸集：
  • \(tx+(1-t)y\in S,~\forall x,y\in S\) 。
  • 不需要是闭的，可以是开的（int C）。
• 正常锥：
  • 锥：x ∈ K 则 θx ∈ K。0 ∈ K。
  • 正常锥：凸 闭 实（非空内部）尖（不包含直线）。
• 对偶锥：
  • 对偶锥： \(K^*=\{y ~|~ x^Ty\ge 0,\forall x\in K\}\) 。
  • 总是凸的。
• 广义不等式：
  • \(x\le_{K}y \iff y-x\in K, ~~ x\lt_{K}y \iff y-x\in \mathbf{int}~K\)。
  • 自反，传递，对加法保序。
• 凸集分离定理：（超平面分离定理）
  • 分离超平面：存在 a b，使得对于 x ∈ C 有 a^Tx ≤ b，x ∈ D 有 a^Tx ≥ b。
  • 凸集分离定理：两个不相交的凸集，总可以用超平面分离。
• 支撑超平面定理：
  • 令 x0 是凸集 C 边界上的一点，对 C 和 x0 使用凸集分离定理。
  • 支撑超平面定理：存在 a，使得对于任意 x ∈ C，均有 a^Tx ≤ a^Tx0 。

2 凸函数

• 凸函数：
  • dom f 是凸集，且对于任意 x y ∈ dom f，任意 θ ∈ [0,1]，有 \(f(θx+(1-θ)y)\le θf(x)+(1-θ)f(y)\) ，即中点的函数值 ≤ 两边的函数值加权平均。
  • 一阶条件：\(f(y)\ge f(x)+\nabla f(x)^T(y-x)\) ；二阶条件：Hessian 矩阵半正定， \(f''(x) \ge0 ~/~ \nabla^2f(x)\succeq 0\) 。
  • 凸函数的例子：
    • 指数函数 e^{ax}，幂函数 x^a，对数函数 log x；
    • 各种范数，矩阵范数，f(x,y) = x²/y，指数和的对数 \(f(x)=\log(e^{x_1}+\cdots+e^{x_n})\)；
    • （凹函数）log det X，（凹函数）几何平均（硬写 hessian 矩阵）。
  • 证明凸函数 1 2 3：
    • 1 定义，2 hessian 矩阵半正定，3 转换到定义域内的直线 x = x0 + tb 这种，变成单变量函数。
  • 强凸函数：f(θx + (1-θ)y) < θf(x) + (1-θ)f(y) ，即在 x ≠ y 且 0<θ<1 时，有严格小于。
• 上境图：
  • \(\mathbf{epi} ~f=\{(x,t)~|~x\in\mathbf{dom} f,f(x)\le t\}\) ，即函数那条线上面（包含线）的区域。
  • 若上境图是凸的，则函数是凸的。
  • 下水平集： \(S_α=\{x\in \mathbf{dom}f ~|~ f(x)≤α\}\)，凸函数的下水平集是凸的。
• 保凸运算：
  • 两个凸函数的 max 还是凸的（逐点 max 或逐点上确界 sup），（非负）加权与（Σw = 1）仿射。
  • 函数复合：
    • 如果 h 是凸函数且非减，g 是凸函数，则 f 是凸函数。
      如果 h 是凸函数且非增，g 是凹函数，则 f 是凸函数。
      如果 h 是凸函数且非减，g 是凹函数，则 f 是凹函数。
      如果 h 是凸函数且非增，g 是凸函数，则 f 是凹函数。

3 凸优化问题

• 凸优化问题：

  • \(\min f_0(x), ~~ s.t.~ f_i(x)\le 0, a_i^Tx=b_i\)，其中 目标函数和不等式约束 凸，等式约束 仿射。
  • 拟凸优化问题：目标函数 f0 是拟凸的。（不过拟凸不考）
  • 范数：1 范数 绝对值相加，无穷范数 取最大分量。

• 转化为凸优化问题：

  • 松弛变量。转化为上境图形式（min t , s.t. f_0(x)-t ≤ 0）。
  • 二范数（x 在一个球内），可以写为 a^Tx ≤ b 的形式。
  • 一范数：\(\min~ y+z, ~~ s.t. ~ y-z=x,~y,z\ge0\) 。则可以得到 |x| 。（不一定常用）
  • 线性分式 \(f_0(x)=(c^Tx+d)/(e^Tx+f), ~~ s.t.~ Gx\le h,Ax=b\) ，转换成 \(c^Ty+dz, ~~ s.t. ~ Gy-hz\le0,Ay-bz=0,e^Ty+fz=1,z\ge 0\) ，其中 \(y=x/(e^Tx+f),z=1/(e^Tx+f)\) 。
  • 变成半正定规划：\(\|A\|_{spec}\le s\iff A^TA\le s^2I\)，其中 spec 是谱范数（最大奇异值，A^TA 最大特征值绝对值）

• 常见问题：

  • 从易到难：LP、QP、QCQP、SOCP、SDP。
  • 线性规划问题（LP）： \(\min c^Tx+d, ~~ s.t. ~Gx\le h, Ax=b\) 。
  • 线性规划的标准形式： \(\min c^Tx+d, ~~ s.t. ~ Ax=b, x\ge 0\) 。
  • 二次约束二次规划（QCQP）： \(\min ~\frac12x^TPx+q^Tx, ~~ s.t. ~~\frac12x^TP_ix+q_i^Tx+r_i \le0, Ax=b\) 。
  • 二次优化问题（QP）： \(\min ~\frac12x^TPx+q^Tx+r, ~~ s.t. ~Gx\le h, Ax=b\) 。
  • 二阶锥规划（SOCP，cone）： \(\min f^Tx, ~~ s.t. ~\|A_ix+b_i\|_2\le c_i^T+d_i,~ Fx=g\) 。
  • 半正定规划（SDP）： \(\min c^Tx, ~~ s.t. ~x_1F_1+\cdots+x_nF_n+G\le 0, Ax=b\) 。
  • 

• 几何规划：

  • 单项式： \(cx_1^{a_1}\cdots x_n^{a_n}\)（其中 c＞0、a 可以为负）。正项式：Σ 单项式。
  • 几何规划： \(\min f_0(x), ~~ s.t. ~f_i(x)\le 1,h_i(x)=1\) ，其中 f 为正项式，h 为单项式。
  • 变成凸优化问题： \(y_i=\log x_i\) 。

4 对偶问题 & KKT 条件

• 对偶问题：
  • 添加松弛 λ fi(x) ，不等式约束是 fi(x)＜0 。
  • lagrange 对偶函数：g(λ,v) = inf_x [L(x,λ,v)]，
    • x 随意变化，使 L(x,λ,v) 取到最小值，即为 g(λ,v)。
  • maximize g(λ,v) subject to λ ≥ 0。
  • 利用 Lagrange 对偶函数，试图找一个最好的下界（最大的、最接近 p* 的下界）。
  • 此时 (λ*, v*) 是 对偶最优解、最优 Lagrange 乘子。Lagrange 最优值写为 d* ，则有 d* ≤ p* 。
  • （不管原问题是什么，对偶问题都是凸问题（？））
• KKT 条件：
  • 因为 L(x,λ*,v*) 关于 x 求极小，在 x* 处取得最小值，因此 L 在 x* 处的导数必须为 0 ，就得到了 KKT 条件。
  • 
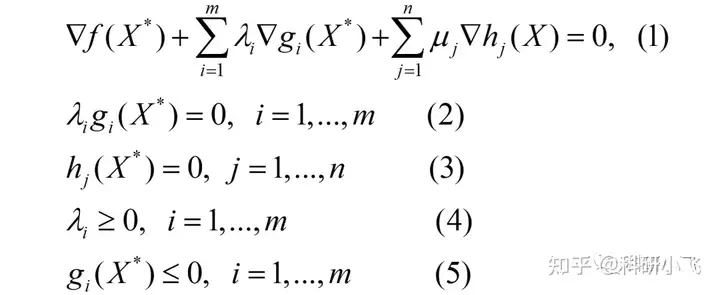
  • 1 在极小值 x* 处的导数为零（鞍点条件），2 要不约束不起作用（λ=0 g≤0）要不约束取等（g=0 λ>0）（也被叫做互补松弛条件），3 5 优化问题原先的等式 不等式约束，4 对对偶变量的约束。
• Slater 条件：（前提是凸优化问题！）
  • 如果存在 x ∈ relint D（D 是定义域），使得 fi(x) < 0 即不等式约束严格成立，那么满足 Slater 条件。
  • 约束集合 C 非空，C 中含有至少一个约束；存在一个满足所有约束的点 x，使得这个点属于 C 的相对内部。
  • 即，存在可行解，在可行域内部 而非边界。
  • 若 Slater 成立，强对偶性成立。是强对偶的充分条件，但不是必要条件。
• 极大极小不等式：\(\sup_z \inf_w f(w,z) ≤ \inf_w \sup_z f(w,z)\)。

5 搜索算法

第 9 章 - 无约束优化：

• 最速下降方法：

  • \(\Delta x_{sd}=\|\nabla f(x)\|_{k^*}\Delta x_{nsd}, ~ \Delta x_{nsd}=\arg\min\{\nabla f(x)^Tv ~|~ \|v\|_{k}\le 1\}\)
  • 使用了神奇的对偶范数。

• 梯度下降方法：

  • \(\Delta x := -\nabla f(x), ~x ← x + t\Delta x\) 。
  • 步长 t 使用 精确 或 回溯直线搜索方法 确定。
  • 回溯直线搜索：
    • 给定 α ∈ (0,0.5)，β ∈ (0,1) ，t 初始化为 1。
    • 若 \(f(x+t\Delta x)>f(x) +αt\nabla f(x)^T\Delta x\)，令 \(t := βt\) 。
    • 否则，直接结束搜索，输出 t 。
  • 精确直线搜索：
    • 射线 \(\{x + t\Delta x ~|~ t ≥ 0\}\)，\(t = \arg\min f(x + t\Delta x)\)。

• Newton 方法：

  • 计算 Newton step 和减量：
    • \(\Delta x_{nt}:=-[\nabla^2 f(x)]^{-1}\nabla f(x), ~~ λ^2:=\nabla f(x)^T[\nabla^2 f(x)]^{-1}\nabla f(x)\) 。
    • 或 \(\lambda^2(x)=\Delta x_{nt}^T[\nabla^2 f(x)]\Delta x_{nt}\) 。
  • 停止准则：如果 \(\lambda^2/2\le\epsilon\) ，退出。
  • 直线搜索：回溯直线搜索，确定步长 t。
  • 改进：\(x\leftarrow x+t\Delta x_{nt}\) 。

第 10 章 - 等式约束优化：

大概的思路是，对于二次近似（貌似是 Newton 法的基本原理？）的优化问题

\[\min ~~~ f(x+v)=f(x)+\nabla f(x)^Tv+\frac12 v^T\nabla^2f(x)v \\ s.t. ~~~ A(x+v)=b ~~~ or ~~~ Av=0 \]

用对偶问题来求解：

\[L(v,w)=f(x+v)+w(Av-b) \\ Av=b, ~~~ \nabla(L(v,w)) = 0 , ~~~\mathrm{that~is} \\ \left[\begin{matrix}\nabla^2f(x) & A^T \\ A & 0\end{matrix}\right] \left[\begin{matrix}\Delta x_{nt} \\ w\end{matrix}\right] =\left[\begin{matrix}-\nabla f(x) \\ 0\end{matrix}\right] \]

• 可行初始点的等式约束 Newton 法：

  • 给定满足 Ax=b 的初始点 x0 、误差阈值 ε。

  • 计算 $Δx_{nt} , ~λ(x) $ 。

    • Newton step \(\Delta x_{nt}\) ： \(\left[\begin{matrix}\nabla^2f(x) & A^T \\ A & 0\end{matrix}\right] \left[\begin{matrix}\Delta x_{nt} \\ w\end{matrix}\right] =\left[\begin{matrix}-\nabla f(x) \\ 0\end{matrix}\right]\) 。
    • 牛顿减量： \(\lambda^2(x)=\Delta x_{nt}^T[\nabla^2 f(x)]\Delta x_{nt}\) 。

  • 停止准则：如果 \(\lambda^2/2\le\epsilon\) ，退出。

  • 直线搜索：回溯直线搜索，确定步长 t。

  • 改进： \(x\leftarrow x+tΔx_{nt}\) 。

• 不可行初始点的等式约束 Newton 法：

  • 给定随便的 x0 ∈ dom f 、误差阈值 ε，回溯直线搜索 α ∈ (0, 0.5)，β ∈ (0, 1) 。

  • 计算原对偶 Newton 方向 \(\Delta x_{nt}, ~ \Delta \nu_{nt}\) 。

  • \[\left[\begin{matrix}\nabla^2f(x) & A^T \\ A & 0\end{matrix}\right] \left[\begin{matrix}\Delta x_{nt} \\ \nu+\Delta\nu_{nt}\end{matrix}\right] =-\left[\begin{matrix}\nabla f(x) \\ Ax-b\end{matrix}\right] \]

  • 对 \(\|r\|_2\) 进行回溯直线搜索。

    • \(t:=1\) 。

    • \[\begin{cases} r(x,\nu) = \big(r_{dual}(x,\nu),r_{pri}(x,\nu) \big) \\ r_{dual}(x,\nu) = \nabla f(x)+A^T\nu \\ r_{pri}(x,\nu) = Ax-b \end{cases} \]

    • 只要 \(\|r(x+t\Delta x_{nt}, \nu+t\Delta \nu_{nt}) \|_2\gt(1-αt)\|r(x,\nu)\|_2\) ，更新 \(t\leftarrow βt\) 。

  • 改进： \(x:=x+t\Delta x_{nt}, ~ \nu:=\nu+t\Delta\nu_{nt}\) 。

  • 直到 Ax = b（近似）且 \(\|r(x,\nu)\|_2\le\epsilon\) 。

第 11 章 - 不等式约束优化：

• （对数）障碍函数：

  • 不等式约束：希望 fi(x) > 0 。（-log 是凸函数）（log 里面的东西 ≥ 0 ）
  • 对数障碍函数： \(\min f(x)-\tau\ln(-f_i(x))\) 。当 τ 足够小时，-τln(-s) = 0 若 s＜0，= +∞ 若 s ≥ 0。
  • （目标函数） \(tJ(x) - \log(-f_i(x) )\) 。t 越大越好。
  • 中心路径（central path）：
    • 中心路径的定义：minimize tf0(x) + Φ(x) 同时满足 Ax=b，这个问题的解 x*(t) 。
    • 需要满足的充要条件：KKT 条件：1. 等式约束成立，2. Lagrange 函数在 (x*, \(\nu\)*) 处的梯度 = 0 成立。
    • 有 \(f_0(x^*(t))-p^*\le m/t\)，其中 t 是障碍函数的 t，m 被障碍函数处理掉的 \(f_i(x)\le0\) 的个数。

• 障碍函数法：

  • 给定严格可行点 x，\(t:=t^{(0)}>0\)， 参数 μ＞1，误差阈值 ε。
  • 从 x 开始，在 Ax=b 的约束下，极小化 \(tf_0(x)+\phi(x)\)，最终得到 \(x^*(t)\) 。
    • 可行初始点 / 非可行初始点的 Newton 法。
  • 改进： \(x=x^*(t)\) 。
  • 停止准则：若 \(m/t\lt\epsilon\) 则退出。
  • 增加 t 的大小： \(t:=\mu t\) 。

• 原对偶内点法（Prime Dual Method）：

  • 初始化：给定满足不等式约束 \(f_i(x)\lt0\) 的 \(x\)，给定初始值 \(λ\succ0, ~~ \mu\gt0\)。两个 ε 都＞0。

    • 确定 t： \(t:=\mu m/\hat\eta\) 。

      • 第 k 次迭代后，代理对偶间隙，\(\hat\eta(x,λ)=-f(x)^Tλ\) 。

    • 计算原对偶搜索方向： \(\Delta y_{pd}\) 。

      • \[y = (x,\lambda,\nu), ~~~ \Delta y=(\Delta x,\Delta \lambda,\Delta \nu) \\ Df(x)=\left[\begin{matrix} \nabla f_1(x)^T \\ \vdots \\ \nabla f_m(x)^T \end{matrix}\right] \\ \left[\begin{matrix} \nabla^2f_0(x)+\sum_{i=1}^m\lambda_i\nabla^2 f_i(x) & Df(x)^T & A^T \\ -\mathrm{diag}(λ)Df(x) & -\mathrm{diag}(f(x)) & 0 \\ A & 0 & 0 \\ \end{matrix}\right]\left[\begin{matrix} \Delta x \\ \Delta \lambda \\ \Delta \nu \end{matrix}\right] = -\left[\begin{matrix} r_{dual} \\ r_{cent} \\ r_{pri} \\ \end{matrix}\right] \]

      • 直接求解。

      • \[r_t(x,\lambda,\nu)=\left[\begin{matrix} r_{dual} \\ r_{cent} \\ r_{pri} \end{matrix}\right]=\left[\begin{matrix} \nabla f_0(x)+Df(x)^Tλ+A^T\nu \\ -\mathrm{diag}(λ)f(x)-(1/t)\mathbf 1 \\ Ax-b \end{matrix}\right] \]

      • 以上分别是 r pre 原误差、r cent 中心误差、r dual 对偶误差。

    • 直线搜索：去确定步长 s＞0。

      • 首先，λ 更新后必须要 ≥ 0，这样得到一个正步长，正步长 = min(正步长, 1)。
      • 然后，开始回溯直线搜索：\(\|r_t(x+\Delta x,\lambda+\Delta \lambda,\nu+\Delta \nu)\|_2\le(1-αs)\|r_t(x,\lambda,\nu)\|\)。
      • 总之就是希望 r 越来越小。
      • 参数：alpha 0.01 - 0.1，beta 0.3 - 0.8。

    • 更新：令 \(y\leftarrow y+s\Delta y_{pd}\) 。

  • 停止准则：直到： $|r_{pri}|2\le \epsilon\mathrm{feas}, ~ |r_{dual}|2\le\epsilon\mathrm{feas}, ~ \hat\eta\le\epsilon $ 。

    • 第 k 次迭代后，代理对偶间隙，\(\hat\eta(x,λ)=-f(x)^Tλ\) 。