复杂系统 | 考前知识点总结（不完全）

这份知识点总结（cheat sheet），是基于 21 级直博师兄的押题（因为我没太听课🥶）；
然而教学大纲比较与时俱进，导致他押题不太准（或许放到两年前是准的叭），所以这份笔记有很多考点没有覆盖（如事件驱动优化 EBO、RL 基础 policy gradient TRPO PPO 等）。

相关链接：

• RL 基础 | Value Iteration 的收敛性证明
• RL 基础 | Policy Iteration 的收敛性证明
• 复杂系统 | 20240116 · 考试题目回忆版
• “嵌套分区法，是一种良策；将海洋分成块，每块都探测。”
• 概述：基于事件的优化方法 / 事件驱动优化 / Event-Based Optimization / EBO

---

目录

• 1 序优化 Ordinal Optimization
  • 1.1 关于 OO 的概率计算
  • 1.2 order 相对 value 的指数收敛
  • 1.3 good enough 相对 optimal 的指数收敛
• 2 Policy Iteration & Value Iteration 的收敛性证明
• 3 排队论 Queueing Theory
  • 3.1 Memoryless Triangle
  • 3.2 简单 M/M/1 系统
  • 3.3 Little's Law
• 4 No Free Lunch
• 5 嵌套分区 Nested Partition
• 6 Alias 算法
• 7 OCBA
  • 7.1 OCBA 算法
  • 7.2 OCBA 的证明

---

1 序优化 Ordinal Optimization

OO 考一个概率或证明指数收敛。

1.1 关于 OO 的概率计算

正态分布的概率密度函数： $f(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$ 。

正态分布相加后的分布：$N({\mu }_1+{\mu }_2,{\sigma }_1^2+{\sigma }_2^2)$ 。

正态分布取 N 均值后的分布：$N(\mu ,{\sigma }^2/N)$ 。

正态分布相乘后的分布：$N({\mu }_1{\mu }_2,{\sigma }_1^2{\mu }_2+{\sigma }_2^2{\mu }_1)$ 。

1.2 order 相对 value 的指数收敛

何教授的 OO 课本的 21 / 33 页。

（每个 design 都满足 $N(J_i,{\sigma }_i^2)$ 的分布。）

放缩：当 k = min(g,s) 时，去证 $Pr\{|G\bigcap S_n|\ge k\}=1-e^{n\beta }$ ，即 $\{|S_n\bigcap G|<min(g,s)\}\le C{e}^{-n\beta }$ 。

定义 Event A 为 达不到完美： $\{|S_n\bigcap G|<min(g,s)\}$ ，就是上面所说的。

定义 Event B 为 循规蹈矩的反面：存在一个 i 使得 $|{\hat{J}}_i-J_i|\ge \delta$ ，δ 是 Δ/2，Δ 是 min |J_i - J_j| 。

若满足 !Event B，就完全没有 misalignment；不过，即使发生 Event B，也可能完全没有 misalignment。

因此，Pr A ≤ Pr B。$Pr[B]=\sum Pr\{|{\hat{J}}_i-J_i|\ge \delta \}\le 2N{e}^{-n\beta }$ 。这里取 β 为各个 β 中最小的。这一步是大偏差理论。

这样就得到了。

1.3 good enough 相对 optimal 的指数收敛

何教授的 OO 课本的 26 / 38 页。

对 blind pick 的 selection rule，希望证明， $Pr\{|S\bigcap G|\ge 1\}=1-O(e^{-gs\beta })$ ，即在 top k 的要求下，k 越松，selection 数量越多，就指数级地越容易。

首先，有 $Pr\{|S\bigcap G|=0\}=C_{N-g}^s/C_N^s$ 。然后，有 $Pr\{|S\bigcap G|\ge 1\}=1-Pr\{|S\bigcap G|=0\}$ 。

对 $Pr\{|S\bigcap G|=0\}=C_{N-g}^s/C_N^s$ 去进行放缩，得到 $(N-g)!(N-s)!/N!(N-g-s)!\le (1-\frac{g}{N}{)}^s\le \exp (-\frac{gs}{N})$ 。

因此得到 $Pr\{|S\bigcap G|\ge 1\}\ge 1-\exp (-\frac{gs}{N})$ 。得证。

对 horse racing 的 selection rule，貌似也可以得到上面的结论。（别看了，就用上面的结论吧。）

2 Policy Iteration & Value Iteration 的收敛性证明

value iteration：https://www.cnblogs.com/moonout/p/17783506.html

policy iteration：https://www.cnblogs.com/moonout/p/17804874.html

DP 收敛到最优解的证明：只要是 MDP、满足无后效性（？），就有 Bellman 最优性原理，最优策略的子策略一定也是最优的。

3 排队论 Queueing Theory

另一个课件，可参考：https://lrita.github.io/images/posts/math/排队论及其应用浅析.pdf

3.1 Memoryless Triangle

好像就是 possion 分布的相关。

我 t 时刻到达车站等车，距前一辆车离开的时间是（听说）什么截尾的指数分布，距后一辆车到来的时间是 指数分布。

证明两辆车到来的时间差 X 满足指数分布，等价于 那是个泊松随机过程。

顾客到达的时间间隔呈指数分布与系统状态呈泊松分布是等效的

基础知识：

• Poisson 分布：一种离散概率分布。
  • $P(X=k)=e^{-\lambda }{\lambda }^k/k!$ 。参数 λ 是单位时间内随机事件的平均发生次数。期望和方差均为 λ 。
  • 适合于描述单位时间内随机事件发生的次数，排队时一定时间内到达的人数。
• Poisson 过程：
  • 一种累计随机事件发生次数的，最基本的独立增量过程。
  • 需要满足三个条件：
  • ① P(X(0)=0)=1。
    ② 不相交区间上增量相互独立，即对一切 $0\le t_1<t_2<\dots <t_n$ ， $X(t_1),X(t_2)-X(t_1),\cdots ,X(t_n)-X(t_{n-1})$ 相互独立。
    ③ 增量 $X(t)-X(s)$ (t>s) 的概率分布为泊松分布。
  • 重要性质：在区间 [t, t + τ] 内发生的事件的数目的概率分布为：$P[(N(t+\tau )-N(t))=k]=e^{-\lambda \tau }(\lambda \tau {)}^k/k!$ ，满足 Poisson 分布。
• Poisson 过程的 Inter-arrival time：
  • 【Poisson 的 memoryless】接下来 t 秒发生事件的概率（无论之前 t0 秒有无发生事件） $P=1-e^{-\lambda t}$ 。
  • 【Constant Arrival rate】接下来 Δt 秒发生事件的概率为 $\lambda \mathrm{\Delta }t+o(\mathrm{\Delta }t)$ ，对于过小的 Δt，o(Δt) 忽略不计。
  • 【Exponential Inter-arrival time】计算前 t 秒内都没有发生事件的概率（或接下来 t 秒都没有发生事件的概率），把 0-t 的事件拆成无穷个 Δt ， $P(t_a>t)=\underset{N\to \mathrm{\infty }}{lim}(1-\lambda \mathrm{\Delta }t{)}^N=\underset{N\to \mathrm{\infty }}{lim}(1-\lambda \frac{t}{N}{)}^N=e^{-\lambda t}$ 。
  • 【Poisson Arrival in [0,t) 】在 interval [0,t] 内发生事件数量，满足 Poisson 分布，有 P(t+Δt 内发生 n 个事件) = P(t 内发生 n 个事件) P(Δt 内没发生事件) + P(t 内发生 n-1 个事件) P(Δt 内发生 1 个事件) 。

Memoryless Triangle - 三者等价：

• Constant Arrival rate；Poisson Arrival in [0,t) ；Exponential Inter-arrival time。

3.2 简单 M/M/1 系统

A：到达时间间的分布。B：服务时间分布。A 和 B 取以下符号集的值，这些符号对应于括号中的分布：M（指数）；Er（r-stage Erlangian）；HR（R-stage 超指数）；D（确定性）；G（一般）。
m：server 数量。K：系统的 storage 容量。M： size of customer population。

MM1：

https://zhuanlan.zhihu.com/p/639097677

基本定义：

• 到达速率和服务速率都是指数分布的；系统中只有一台服务器；缓冲区大小是无限的。
• 到达速率：A，单位时间内到达请求数量 λ，$f_a(\tau )=\lambda \exp (-\lambda \tau )$。
• 服务速率：B，单位时间内处理请求数量 μ，$f_b(\tau )=\mu \exp (-\mu \tau )$。
• ρ = λ/μ 。

分布：

• 在时间 t 内到达的顾客总数 k，是一个泊松事件过程。在时间 t 到达的顾客呈泊松分布。
• 

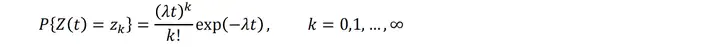
重要公式：

• Average number of customers in the system N = ρ/(1-ρ)
• Average time in system τ_d = 1/(μ-λ)
• Average waiting time W = ρN/λ
• Average time in system = average waiting time + average service time (1/μ).

应用 Little's Law 做计算：

N = λ * 1/(μ-λ) ，N = average time in system * customer arrival 。

3.3 Little's Law

在一个稳定的系统中，长期的平均顾客人数（N），等于长期的有效抵达率（λ），乘以顾客在这个系统中的平均时间（T）。或者，我们可以用一个代数式来表达：N = λT。

（队列长度 = 平均到达率 单位时间到多少人 × 人在系统内的平均时间）

虽然此公式看起来直觉性的合理，它依然是个非常杰出的推导结果，因为此关系式“不受到货流程分配、服务分配、服务顺序，或任何其他因素影响”。

直观证明：

• t 内的最后一个到达将在 (t+ε) 离开系统。所以 arrival(t) = departure(t+ε) 。（a 和 d 是现在到达 / 离开的总人数）
• 因此，N(t) = a(t) - d(t) = d(t+ε) - d(t)。
• 在稳定状态下，ε=T（即平均通过排队系统的时间（排队时间？）为 T），出发率 = 到达率 = λ 。
• 所以 N(t) = d(t+ε) - d(t) = λ(t+ε) - λ(t) = λT。

写公式来证明：

$$\begin{gathered} {\int }_0^{t}N(\tau )d\tau =\sum _{i=1}^{a(t)}{T}_i-ϵ \\ T=\underset{t\to \mathrm{\infty }}{lim}\frac{\sum _{i=1}^{a(t)}{T}_i}{a(t)};\lambda =\underset{t\to \mathrm{\infty }}{lim}\frac{a(t)}{t};N=\underset{t\to \mathrm{\infty }}{lim}\frac{{\int }_0^{t}N(\tau )d\tau }{t}; \\ \underset{t\to \mathrm{\infty }}{lim}\frac{{\int }_0^{t}N(\tau )d\tau }{t}=\underset{t\to \mathrm{\infty }}{lim}\frac{\sum _{i=1}^{a(t)}{T}_i}{a(t)}\times \underset{t\to \mathrm{\infty }}{lim}\frac{a(t)}{t}-\underset{t\to \mathrm{\infty }}{lim}\frac{ϵ}{t}; \\ \underset{t\to \mathrm{\infty }}{lim}\frac{ϵ}{t}=0 \end{gathered}$$

• 第一行：N(tau) 是 tau 时刻系统内的人数。a(t) 是来人的函数，单调递增。ε 是 最后一个人还有多久走（见 slides 57 页的图）。第一行的意思是，系统内人数的积分（即 从 0 到 t 都来了多少人） = a(t) 个来的人都分别呆了多久 - ε。
• 第二行：每个人平均在系统内呆的时间 T 的计算。λ：长远来看（t → 无穷）平均每时刻来多少人。N：每一时刻在系统内的人数 / 总共过去的时间 = 每时刻平均有多少人在系统内（感觉像平均值）。
• 第三行：假装可以拆成这样的极限相乘吧（不会证）。
• 第四行：是显然的。ε 再大也是有限量，跟 lambda mu 是一个量级的（大概）。

4 No Free Lunch

直接看课件吧。问题：简单解释 No Free Lunch 定理。

回答：

1 我们考虑简单的 状态空间离散化且有限的 问题场景。假设 x（N 维）是优化变量，f 是性能函数（简化考虑，只可能输出两个值，1 好 0 坏），y = f(x) 为性能。我们希望寻找 x，使得 f(x) = 1。

所有的 f 有 2^N 种。可以列一个 x × f(x) 的 N × 2^N 维度的矩阵，代表所有的 f。如果我们对我们的问题的结构一无所知，那么就不知道 f 在矩阵的哪一列，可以视为对矩阵的所有列求平均的期望。这样的话，无论如何选择 x，其性能的期望都不会比 blind pick 更好。对于连续的情况，也是一样的。

2 更危险的情况是，如果我们知道一些关于最优解的先验。比如说，我们听说 f 矩阵左边的列是相对更优的，去选择左边的列作为问题结构的先验。如果这一知识是正确的，那么情况是好的。如果这一知识错误，相对更优的列在其他位置，那么左边的列其实会相对更差，会导致我们的性能比 blind pick 更差。

3 同时，若想寻找最优解，那么会受到维度灾难的影响：寻找最优解的复杂度，随着问题规模而指数增加。

4 因此，优化是复杂的，利用启发式的先验来解决问题，也是脆弱的。有两个方法可以缓解这种问题：1. 比较序而非值，2. 选择足够好而非最优。同时，可以利用问题结构，将问题建模成分层或分模块的形式，以简化空间。

5 嵌套分区 Nested Partition

估计会考 nested partition 找最优解的模拟。

一个部分错误的算法：https://www.cnblogs.com/moonout/p/17962129

Nested Partition 算法：

• 第一步，初始化。选择一个初始的可行解空间 X，设定分区的层数 d 和每层的分区数 M，设定停止条件。
• 第二步，分区（partitioning）。将当前的可行解空间 X 分解为 M 个子区域，记为 X_1, X_2, ..., X_M，并保留一个补充区域 X_M+1，包含 X 中剩余的解。
• 第三步，采样。在每个子区域中随机生成（按一定规则生成）若干个可行解，记为 x_1, x_2, ..., x_M，以及 x_M+1。
• 第四步，评估。计算每个可行解的目标函数值 f(x_i)，并根据一定的规则（课件上直接采取最佳值 min f(x) ），确定每个子区域的期望指标（promising index）g(X_i)，用于衡量子区域的优劣。
• 第五步，选择。比较每个子区域的期望指标 g(X_i)，找出最大（或最小）的一个，记为 g(X_j)，并将对应的子区域 X_j 作为最有希望的区域。
• 第六步，更新。
  • 如果满足停止条件（达到最大迭代次数、最优解的改善量小于阈值、最 promising 的区域已不能再分解），则停止算法，输出当前的最优解 x_j 。
  • 如果当前 promising index 比之前找到的最大（最小）值小（大），则回溯到之前最 promising 的区域。
  • 否则，将可行解空间 X 更新为 X_j，回到第二步，继续分区。

6 Alias 算法

别名算法 Alias 算法，必考，证明和操作。出条件，把 r 和 a 写出来。

• https://zhuanlan.zhihu.com/p/54867139（不如第二个可读）
• https://zhuanlan.zhihu.com/p/111885669
• https://zhuanlan.zhihu.com/p/591782173（有证明，思路是对的，但感觉说的不够清楚）
• https://blog.csdn.net/rover2002/article/details/106760664

证明一定能把 $\sum _{i=1}^N{p}_i=N$ 分到 N 个桶里，使得每一个桶最多有两种东西。

• K = 1 显然。
• K → K+1：若 pi = 1 则每个桶一个。
• 否则，一定存在一个 $p_{K+1}<1$，并且存在 $p_1$ 使得 $p_{K+1}+p_1\ge 1$ ，否则 $\sum _{i=1}^N{p}_i\le \sum _{i=1}^N(p_i+p_{K+1})<\sum _{i=1}^{N}1=N$ ，又有 $p_{K+1}<1$，无法满足 $\sum _{i=1}^N{p}_i=N$ 。
• $p_{K+1}$ 去掠夺 $p_1$ ，使得第 K+1 个桶被填满。然后对前 K 个桶执行 K=K 的算法。数归得证。

更快的证明：

def create_alias_table(area_ratio):
    # 根据概率分布乘以 N 的结果，构建 accept 和 alias 数组
    l = len(area_ratio)
    accept, alias = [0] * l, [0] * l
    small, large = [], [] # 存储面积小于 1 和大于 1 的事件的索引
    for i, prob in enumerate(area_ratio):
        if prob < 1.0:
            small.append(i)
        else:
            large.append(i)
    while small and large: # 将大于 1 的事件的多余部分分配给小于 1 的事件
        small_idx, large_idx = small.pop(), large.pop()
        accept[small_idx] = area_ratio[small_idx]
        alias[small_idx] = large_idx
        area_ratio[large_idx] = area_ratio[large_idx] - (1 - area_ratio[small_idx])
        if area_ratio[large_idx] < 1.0:
            small.append(large_idx)
        else:
            large.append(large_idx)
    while large: # 处理剩余的大于 1 的事件，将其 accept 设为 1
        large_idx = large.pop()
        accept[large_idx] = 1
    while small: # 处理剩余的小于 1 的事件，将其 accept 设为 1
        small_idx = small.pop()
        accept[small_idx] = 1
    return accept, alias

7 OCBA

7.1 OCBA 算法

• 总的 budget 是 T。先为每个 design 分配 n0 个 simulation。
• 然后，设置每次的新 budget allocation：
  • "将计算预算（即额外模拟的数量）增加 A"，比如 10 个 10 个增加。
  • 对 i ≠ j ≠ b，设置 $\frac{N_i}{N_j}=(\frac{{\sigma }_i/{\delta }_{b,i}}{{\sigma }_j/{\delta }_{b,j}}{)}^2$ 。（signal-noise ratio rule）
  • 对当前的最优 design b（ ${\overline{J}}_b\le {\overline{J}}_i,i\ne b$ ），计算 $N_b={\sigma }_b\sqrt{\sum _{i=1,i\ne b}^k{N}_i^2/{\sigma }_i^2}$ 。
  • 大概是，先对所有 i j ≠ b 设置 budget allocation（可以设置那个比值 = k），然后再计算 b 的 budget allocation（= 常数 × k）。（应该是可以做到的）
• 然后，分配 simulation budget：新增 $max(0,N_i^{l+1}-N_i^l)$ 。

7.2 OCBA 的证明

OCBA 证明：希望在有限次 simulation 下最大概率找到最优解，1. 放缩找到最优解的概率，得到一个下界，2. KKT 条件 拉格朗日松弛 得到 N（计算量）如何分配。

假设 tilde J 是给定了观测的均值方差的 真实 performance 的后验分布。

第一步，放缩：$P\{CS\}=P\{\bigcap _{i=1,i\ne b}^k({\tilde{J}}_b-{\tilde{J}}_i<0)\}\ge 1-\sum _{i=1,i\ne b}^{k}P\{{\tilde{J}}_b>{\tilde{J}}_i\}=APCS$ ，approximate PCS。

然后转化问题，把 Ni ≥ 0 的约束条件去掉（？），让 Ni 可以取任意实数值。

第二步，Lagrange 松弛：（F 其实就是 Lagrange 函数 L）

$$\begin{gathered} \underset{N_1,\cdots ,N_k}{max}1-\sum _{i=1,i\ne b}^{k}P\{{\tilde{J}}_b>{\tilde{J}}_i\} \\ s.t.\sum _{i=1}^k{N}_i=T. \\ F=1-\sum _{i=1,i\ne b}^k{\int }_{-\frac{{\delta }_{b,j}}{{\sigma }_{b,j}}}^{\mathrm{\infty }}\frac{1}{\sqrt{2\pi }}{e}^{-\frac{t^2}{2}}dt-\lambda (\sum _{i=1}^k{N}_i-T) \end{gathered}$$

然后直接硬写 KKT 条件：

$$\frac{\partial F}{\partial N_b}=\frac{-1}{2\sqrt{2\pi }}\sum _{i=1,i\ne b}^k\exp [\frac{-{\delta }_{b,i}^2}{2{\sigma }_{b,i}^2}]\frac{{\delta }_{b,i}{\sigma }_b^2}{N_b^2({\sigma }_{b,i}^2{)}^{3/2}}-\lambda =0$$

考察 Nb 与 Ni 的关系，可以直接得到 $N_b={\sigma }_b\sqrt{\sum _{i=1,i\ne b}^k\frac{N_i^2}{{\sigma }_i^2}}$ 。

考察 Ni 与 Nj 的关系，令 T 趋于无穷，可以得到 $\frac{N_i}{N_j}=(\frac{{\sigma }_i/{\delta }_{b,i}}{{\sigma }_j/{\delta }_{b,j}}{)}^2$ 。

（具体公式懒得抄，感觉也背不过…）