cs 保研经验贴 | 综合面试题库

绝大部分夏令营都需要面试：如果幸运的话，稍微问几个问题就结束了；不幸的话，可能要抓住你做项目、读论文、复现、做 pre 等等。

这篇博客适用于幸运的情况：绝大部分学校的面试题库，都是彼此重合的，并且一年年的没什么变化。因此，只要准备一下常见的高频问题，就足以应付这种面试了。

---

目录

• 夏令营原题：数学
  • 线代
  • 概率论
  • 高数
  • 离散数学
• 夏令营原题：专业课
  • 数据结构
  • 机器学习
  • 操作系统（非重点）
  • 计算机网络（非重点）
  • 数据库（非重点）
  • 计算机组成原理（非重点）
  • 编译原理（非重点）
  • 其他

---

同站相关博客：

• cs 保研经验贴 | 数学试题 · 自动化所特供版
• cs 保研经验帖 | 英语口试
• 线性代数 | 等价 · 相似 · 合同
• 线性代数 | 最小二乘法的直观理解
• 高等数学 | 数列 函数 级数 函数项级数之收敛性（上）
• 高等数学 | 数列 函数 级数 函数项级数之收敛性（下）

---

夏令营原题：数学

线代

• 【北航】矩阵的范数：

  • 引入范数的目的是为了度量。
  • 正定（零矩阵范数=0），齐次（|λA|=λ|A|），三角不等式（两边范数之和 ≥ 第三边范数）。
  • 对于矩阵范数，还有：||AB|| ≤ |A|·|B|

• 【北航】线性无关是什么：

  • 一组向量里面，没有一个可以被其他人联合表示。
  • 只有当 k全=0 时，Σkx=0 才成立。
  • 广义 组成的四边形 六面体 超几何体 体积是否不为零。
  • 线性组合：多项式，全是一次项（无向量相乘 无常数）。

• 【北航】矩阵的行列式：

  • 广义平行四边形的体积。
  • 行列式为零的矩阵，不可逆（把线性无关的向量，映射成线性相关的了，丢失信息 则不可逆）；行列式不为零的矩阵，可逆。

• 【北航】矩阵的迹：矩阵主对角线元素的和

• 【ALL】矩阵的秩是什么，有什么物理意义

  • 矩阵中线性无关向量的个数。
  • 取子矩阵（方阵）的行列式，最大子矩阵维度 使得行列式 ≠ 0。
  • 物理意义：方程有几个解。
  • 秩：变换后，虽然可能没法完全不丢信息，但至少还能给你保住几个面。
  • r(AB) <= r(A), r(A) + r(B) - n <= r(AB)
  • 矩阵可逆 <=> 矩阵满秩。

• 【北航】Ax=b有解的条件：

  • A 的秩 = 分块矩阵 (A,b) 的秩
  • 如果 b 存在于 A 的列向量的线性空间中，则有解，否则无解；
  • 如果 A 的列均是线性无关的（列满秩），那么存在唯一解；非列满秩则多解；
  • Ax=0 如果列满秩，则只有零解。

• 【北航】【复旦】矩阵的特征值是什么，有什么物理意义，应用

  • Ax=λx。算子的本征值（投影不变，有点像傅里叶变换 卷积指数信号还是指数信号）。
  • —个变换矩阵的所有特征向量，都是正交的，组成了这个变换矩阵的一组基。
  • 矩阵的特征值分解：\(A=Q\Sigma Q^{-1}\)，Σ是对角阵，Q是特征列向量组成的矩阵。
  • 怎么求：
    • 写出方程丨λE-A丨=0，其中I为与A同阶的单位阵，λ为代求特征值
    • 将n阶行列式变形化简，得到关于λ的n次方程
    • 解此n次方程，即可求得A的特征值
  • 应用：PCA 主成分分析。

• 【自动化所】【北航】线性空间是什么，m维线性空间的定义

  • m个相互正交的向量，做加法和数乘，可以组成线性空间。
  • 向量空间：V 为 n 维向量的集合，不为空集，对加法和数乘封闭。
  • 线性空间：再满足
    • 向量加法 交换律 结合律，数乘结合律，加法和数乘的分配律。
    • 向量加法的零元素 向量加法可逆（负数），数乘的 1 元素。

• 【软件所】转置矩阵的几何意义

  • 二维图像 关于某个点对称后（关于 45° 轴翻转？）。

• 【北航】正交矩阵：

  • \(AA^T=A^TA=E\)，\(A^T\) 是 \(A^{-1}\) 也是正交矩阵，行向量 列向量是单位向量 且两两正交，|A|=1 或 -1（显然）。
  • 左乘正交矩阵造成的空间变换，是用一个新空间代替原有空间，即用另一组正交基描述被变换的向量，不改变原向量的长度和空间位置。

• 【北航】矩阵如何求逆：

  • 待定系数法，初等变换法：

• 【北航】什么时候 AB = BA：

  • P−1AP，P−1BP 都是对角阵（同一个P），或者A=B。

概率论

• 【北航】【北大】贝叶斯公式是什么，有什么应用

  • 已知 B 求 A 的概率，等于 AB 都发生概率 / B 发生的概率。
  • 已知事情发生了，求 xx 事情是因的概率。也就是似然？

• 【北航】期望和方差的定义：

  • 

• 【北航】全概率公式：

  • 事件 A1，A2，…构成一个完备事件组，才能用全概率公式。

• 【复旦】【22年复旦又问到了！】最大似然估计

  • 概率：结果没有产生之前，根据环境参数，预测某件事情发生的可能性；
  • 似然：在确定的结果下，去推测产生这个结果的可能环境参数。
  • L(θ|x) = P(x|θ)。

• 【复旦】【北航】解释独立性、相关性、互斥性；

  • 独立 互不影响 条件概率=概率，互斥 不能同时发生。
  • 条件独立：P(AB∣C)=P(A∣C)P(B∣C)
  • 协方差：两随机变量 线性相关性的强度，\(Cov(X,Y)=E{[X−E(X)][Y−E(Y)]}\)，相关系数 归一化（不受变量尺度影响）\(Cov(X,Y)/\sqrt{D(X)}\sqrt{D(Y)}\)。
  • 独立一定不（线性）相关，不相关不一定独立。服从二维正态分布，不相关 <=> 独立。举例，Y=X²。

• 【北大】【北航】大数定律，中心极限定理：

  • 大数定律：当样本数据无限大时，样本均值趋于总体均值。事件 A 发生的频率逼近于它的概率。切比雪夫（样本均值→总体均值），伯努利（频率→概率），辛钦（样本均值→期望）。
  • 中心极限定理：当样本量 n 逐渐趋于无穷大时，n 个抽样样本的均值的频数，逐渐趋于正态分布。原总体的分布不做任何要求。
  • 中心极限定理 应用：蒙特卡罗法。求随机变量之和Sn落在某区间的概率。

• 【msra】熵是什么

• 【北航】【复旦】高斯分布（正态分布）是什么

  • 若随机变量 X 服从一个数学期望为 μ、方差为 σ² 的正态分布，记为 N(μ, σ²)。
  • 概率密度函数：
  • 期望值μ决定了其位置，标准差σ决定分布的跨度。μ = 0, σ = 1：标准正态分布。
  • 正态分布能积分出来吗：不太能，最多只有这个
  • 应用场景：近似某些分布（中心极限定理），把成绩转换为正态分布（高考赋分）。

• 【北航】概率密度函数 是什么：

  • 连续型随机变量，落在一段区间的概率 / 区间长度 取极限。

• 【北航】二项分布，超几何分布。

  • 二项分布：n次独立重复的伯努利试验中，设每次试验中事件A发生的概率为p。n 次试验中事件 A 恰好发生 k 次，这个离散概率分布。 \(P\{X=k\}=C_n^kp^k(1-p)^{n-k}, C_n^k=\frac{n!}{k!(n-k)!}\)
  • 超几何分布：它描述了从有限N个物件（其中包含M个指定种类的物件）中抽出n个物件，成功抽出 该指定种类 的物件的次数（不放回）。

• 【北航】泊松分布：

  • 泊松分布： ，参数λ是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
  • 举例：医院平均每小时出生6个新生儿，想知道在起飞前一小时 是否有机会见到10个或更多的婴儿。预测这段时间来的客户数量。
  • 当二项分布 n 很大 p 很小时，泊松分布可作为二项分布的近似，其中 λ 为 np。

高数

• 【北航】【自动化所】可微与可导有什么区别，一维 二维 条件，与连续的关系。

  • 可微：若自变量在点x的改变量Δx，与函数相应的改变量Δy，有关系Δy=A·Δx+ο(Δx)，其中A与Δx无关。那么 A 是微分。
  • 可微：偏导数 在邻域 存在且连续。
  • 可导：lim Δy/Δx =A 存在，那么 A 是导数。两侧可导则连续。
  • 连续：一维：可微<=>可导=>连续=>可积，多维：可微=>偏导数存在=>连续=>可积。

• 【自动化所】【北航】【复旦】连续和一致连续，收敛和一致收敛

  • 连续 函数，收敛 级数。
  • 连续：某点连续：极限值=函数值（不会跳变），函数连续：每个点都连续。
  • 一致连续：对区间 I 上任意两点 x1 x2，当 |x1-x2|<δ 时，|f(x1)-f(x2)|<ε。
  • 一致连续→连续，1/x 不一致连续。考察均匀程度，不允许难以接受的连续突变（特别陡）。闭区间上，连续<=>一致连续。
  • 收敛：对特定的x，级数项数→无穷时，极限值=某个函数(x)。
  • 一致收敛：
  • 收敛：在极限函数 的任意小邻域内（该邻域对 x 定制）（可以想象成一条加宽的带子），对于函数列 ， 项之后的函数图像都会全部落在这条带子里面。一致收敛：对所有 x，找到一条通用的带子。
  • 收敛→一致收敛，fn(x)=x^n (0, 1) 上收敛到 0，但不一致收敛。不允许 |fn(x)-f(x)| 难以接受的大。闭区间上，收敛<=>一致收敛。
  • 一致收敛后，对和函数求积分 可以变成 逐项求积分求导。

• 【自动化所】【北航】柯西中值定理，拉格朗日中值定理

  • lagrange：闭区间连续 开区间可导，切线割线斜率。
  • cauchy：闭区间连续 开区间可导，g' ≠ 0，割线相比 = 导数相比。

• 【自动化所】牛顿迭代法

• 【自动化所】【北航】最小二乘法

• 【复旦】【北航】极限的定义：

  • epsilon-N 定义，epsilon-δ 定义。趋于∞：M(大数)。

• 【北航】边缘分布：

  • P(x)=Σ_y P(x,y)=Σ_y P(x|y)P(y)

• 【复旦】空间闭环曲线 怎么求面积或体积；

  • green gauss stokes。

• 【计算所】【北航】如何计算Sin 1

  • 如果是 sin 1° / sin 1/180Π，直接泰勒级数。
  • 如果是 sin 1，泰勒级数可能不太行（1 的多少次方还是1）（并不，从网上查的是ok的），可能要 sin1=2cos0.5sin0.5，再泰勒展开？

• 【北航】极大值什么时候等于最大值

  • 导数单调递减，即二阶导数＜0，上凸函数，肯定 ok。
  • 考察最大的极大值和端点值的关系。（端点值＞极大值，且开区间，则无限逼近端点，函数无最大值）

离散数学

• 【北航】握手定理：

  • 有n个人握手，每人握手x次，握手总次数为 S= nx/2。

• 【北航】命题逻辑的连接词：

  • 一元连接词：非¬
  • 二元连接词：合取 ∧，析取 ∨，异或 ⊕，蕴涵 →，等价 <->。

• 【北航】单射（我和你各抢各的 不抢一个人），满射（所有人都被抢了），双射（一一对应）。

• 【北航】幂集，笛卡儿积：

  • 幂集：原集合中所有的子集（包括全集和空集）构成的集合，集合的集合 N → 2^N。
  • 笛卡尔积：第一个对象是X的成员，第二个对象是Y的成员，所有可能有序对的集合。

• 【北航】偏序关系：

  • 非严格偏序或自反偏序：

    • 给定集合S，“≤”是S上的二元关系，满足：
    • 自反性：∀a∈S，有a≤a；
    • 反对称性：∀a，b∈S，a≤b且b≤a，则a=b；
    • 传递性：∀a，b，c∈S，a≤b且b≤c，则a≤c；则

  • 严格偏序，反自反偏序：

    • 反自反性：∀a∈S，有a≮a；
    • 非对称性：∀a，b∈S，a<b ⇒ b≮a；
    • 传递性：∀a，b，c∈S，a<b且b<c，则a<c；

• 【北航】欧拉回路，哈密顿回路。

  • 哈密顿回路：经过每个点一次并且回到起点（旅行商问题），NP-complete 也是 NP hard。
  • 欧拉回路：经过每一条边并回到起点，一笔画。
    • 图是连通的，没有孤立节点，（欧拉通路）对于无向图，奇数度的顶点为2个（起点终点），剩下都是偶数度。如果没有奇数度顶点，可以有欧拉回路。

• 【北航】等价关系：

  • 设 R 是集合 A 的二元关系，R 自反 对称 传递 → 等价关系。
  • 自反性：∀a∈S，有 aRa；
  • 对称性：在集合R中，若 aRb 则 bRa。
  • 传递性：∀a，b，c∈S，aRb 且 bRc，则 aRc；

• 【北航】图 度数和边的关系

  • 有向图：入度 出度。边数=Σ入度=Σ出度
  • 无向图：边数=0.5 Σ度

• 【北航】集合的划分，集合的基：

  • 划分可能就是所谓完备事件集？互不相交，并集=原集合。基貌似是集合元素个数。

• 【北航】群 环 域：二元运算

  • 群：加法，封闭性 结合性 单位元 反元素。
  • 环：在交换群的基础上，添加二元运算乘法：加法单位元是乘法零元素，反元素 (-a)b = a(-b) = -(ab)，结合律（半群），关于加法满足分配率。
  • 域：在交换环的基础上，增加二元运算除法，具体没有学。

夏令营原题：专业课

强意向：自动化系。自动化所，计算所，人大高瓴，北航，上交，复旦，天大。

弱意向：软件所，北理工，南开。

无意向：清华其他地方，北大，南大。

数据结构

• 【复旦】快排时间复杂度（最优最差和平均），证明
• 【高瓴】【2022年高瓴又考到了！】KMP 字符串匹配
• 【北航】栈算表达式，前缀中缀后缀表达式
  • 中 → 后：两个栈。
  • 计算后缀表达式：一个栈。
  • 计算前缀表达式：从右到左（反向）扫描，数字压栈，运算符 弹栈*2 计算。
• 【北大】【复旦】【北航】常见的排序算法，复杂度
  • 稳定 / 非稳定排序：两个相等的数 排序前后 相对位置不变。
  • 插入排序（希尔排序）：
    • 每一趟将一个待排序记录，按其关键字的大小插入到已排好序的一组记录的适当位置上，直到所有待排序记录全部插入为止。稳定，O(n)，O(1)。
    • 把记录按下标增量（模）分组，对每组进行直接插入排序，每次排序后减小增量，当增量减至 1 时排序完毕。不稳定，不知道（有个实验结论），O(1)。
  • 冒泡排序：
    • 比较相邻的元素，如果第一个比第二个大就进行交换，对每一对相邻元素做同样的工作。稳定，O(n)，O(1)。
  • 选择排序：
    • 每次在未排序序列中找到最小元素，和未排序序列的第一个元素交换位置，再在剩余未排序序列中重复该操作，直到所有元素排序完毕。不稳定，O(n)，O(1)。
  • 桶排序：
    • 将数组分到有限数量的桶里（比如按照十进制最高位，分到10个桶里），每个桶分别排序（可能使用别的排序算法，也可能递归桶排序），然后把排序好的桶连接起来。
    • 稳定。桶数量 = 数据量时，O(N)，O(N)。桶数量 = 2，完全递归桶排序，O(NlogN)，O(N)。
  • 归并排序：
    • 将待排序序列分成两部分，先对两部分 分别递归排序，然后进行合并。稳定，O(nlogn)，O(n)。
  • 堆排序：
    • 堆是一种完全二叉树，最大值堆：子节点均小于父节点，最小值堆：子节点均大于父节点。
    • 插入：放在完全二叉树最后一点，一直往上升。
    • 删除：取出根节点，最后一点升顶，往下降。
    • 不稳定，O(nlogn)，O(1)（树状数组）。
  • 快速排序：
    • 随机选择一个基准元素，通过一趟遍历 将要排序的数据分割成两部分，一部分全部小于等于基准元素，一部分全部大于等于基准元素，继续对两部分递归快排。不稳定，O(nlogn)，O(1)。
    • 最优：每一次选基准元素都恰好选到中位数，⼆叉树的层数（logn）即为递归需要进⾏的次数，并且每轮递归结束时，都将⼆叉树遍历了⼀遍（n），O(nlogn)。
    • 最差：数组完全倒序，每次都选到最大的作基准，O(n^2)。
    • 平均：
    • 
    • 然后错位相减：nA(n) - (n-1)A(n-1)
    • 
• 【复旦】用栈实现 Hanoi：
  • 实现：应该指盘子堆叠 LIFO。
  • Hanoi：将 A 上面的 n-1 个盘子移到 C 上，即 A(n-1) 次；将第 n 个盘子移到 B 上，1 次；将 B 上面的 n-1 个盘子移到C上，即 A(n-1) 次。A(n) = 2A(n-1) + 1。
• 【北航】贪心算法得不到最优解的例子
• 【复旦】最短路径有几种算法，复杂度
  • Floyd：求所有点到所有点的最短路径。
    • for 源点 i，for 终点 j，for 松弛点 k，d[i][j]=min(d[i][j], d[i][k]+d[k][j])，O(n^3)。
  • Dijkstra：求原点到所有点的最短路径，正边权图。
    • 选择目前仍未确定最短路的 距离最短顶点 k（堆优化），确定 k 和 k 的前向，别的顶点对 k 松弛一遍 d[j]=min(d[j], d[k]+edge[k][j])，O(ElogV)，E：对每条边都松弛一遍，logV：入堆出堆。
• 【复旦】最小生成树（MST）是什么，怎么求。
  • 一个联通子图，包含所有结点，边数 = n-1，边权之和最小。存在多个。
  • prim（点 稠密图）：每次选择 与连通块之间的边权值最小的顶点（堆），直到已选 n 个顶点。维护 {边权, 边顶点1, 顶点2} 的结构体，用堆来存，每次 logV 选最小顶点，选完更新其他顶点（旧信息出堆，新信息入堆，Σ边数×logV，常数为最大度），O((E+V)logV)。
  • kruskal（边 稀疏图）：每次选择 两顶点未连通（并查集）权值最小的边，直到已选 n-1 条边。边按权值排序 然后依次选边，O(V+ElogE) 排序 。
• 【北航】从海量数据里找到一个相对大的数
  • 分块，分成1000块，找每块里最大的 K 个数，再把这 1000K 个数进行排序。
• 线性表：数组，链表，栈，队列。
• 二叉树：满二叉树（每一层都最大节点数量），完全二叉树（一行行排），二叉搜索树，前中后序 层序 遍历。
• AVL 树（二叉平衡树）：改进的搜索二叉树。
  • 每一个结点的左右分支绝对高度不超过1，（1为平衡因子）。
  • 增删后，通过旋转的方式重新恢复平衡。
• 图的邻接表：通过链表存储图的连接关系。本顶点存在表头，相邻顶点依次以单向链表形式存在后面，V 个链表。适合稀疏图。
• DFS / BFS：
  • DFS：将图中每个顶点的访问标志设为 false，之后搜索图中每个顶点，如果未被访问，则以该顶点 V 为起始点出发，访问 V，依次递归 DFS 访问 V 的各个未被访问邻接点，直至图中所有和 V 连通的顶点都被访问到。（栈）
  • BFS：从图中某顶点 V 出发，访问此顶点后，依次访问 V 的所有未访问邻接点，之后，按这些顶点被访问的先后次序，依次访问它们的邻接点，直至图中所有和 V 连通的顶点都被访问到。（队列）
• 【高瓴】无向图求割点。
  • 割点 / 关节点：
    • 若删除某个节点 u 和它带有的边，连通分量数目增加。
    • 若生成树中某个非叶子顶点V，其某棵子树的根和子树中的其他节点，均没有指向V的祖先的回边，则V为关节点。因为删去v，则其子树和图的其它部分被分割开来。
  • Tarjan 复杂度 O(V+E)：
    • dfn 数组 维护从某节点开始 dfs 的访问顺序。
    • low 数组 维护某节点 dfs 能访问到的最小 dfn 节点，也就是最祖先的节点；平常。
    • 先 dfs，没点了 / 该点是祖先 回溯，回溯过程中，修改父亲节点 low = 子节点 low。
    • 如果一个父节点 v 的子节点 c 的 low[c] ≥ dfn[v]，即我除了 连父节点的环，就没有连更早的祖先，那么 v 是割点。如果 low[c] > dfn[v]，即 我没有连回任何祖先的环，则 c - v 是割边。
    • （为什么没有连到其他更年长的兄弟的环呢？因为如果有，无向图 则兄弟 dfs 时就会遍历到我，并且遍历到父节点，从而拥有了连到父节点的环。）

机器学习

• 【复旦】列举比较常见的聚类算法，K-means 原理，除了 K-means 还有什么聚类算法

  • K-means：

    • 选择初始化的 k 个样本作为初始聚类中心 ；
    • 对数据集中每个样本 ，计算它到 k 个聚类中心的距离，并将其分到聚类中心距离最小的类别；
    • 针对每个类别 ，重新计算它的聚类中心 （该类所有样本的质心)；
    • 重复上面两步操作，直到达到某个中止条件（迭代次数、最小误差变化等）。

  • 优：容易理解，效果不错，复杂度低

  • 劣：容易陷入局部最优，K 值需人为设定，对初始聚类中心敏感，对异常值敏感，不适合非凸形状聚类。

  • 其他聚类算法：

    • 均值偏移 mean shift 更密集的地方 滑动窗口
    • 
    • 层次聚类：自下而上，一开始将每个数据点视为单一的聚类，然后依次合并。

• K 近邻（KNN）：

  • 给一个新数据，通过与它离得最近的 K 的样本 类别 投票，决定它是什么类别。
  • 优：模型不用训练，对异常值不敏感。
  • 劣：模型预测复杂度为 O(已有数据个数)，K 值有影响，或许不适合很多特征。

• 【北航】谈一谈梯度下降

• 【北航】最小二乘法：

  • 最小二乘法是解决曲线拟合问题最常用的方法。其基本思路是：令

    

    其中，

    

    是事先选定的一组线性无关的函数，

    

    是待定系数

    

    ，拟合准则是使

    

    与

    

    的距离

    

    的平方和最小，称为最小二乘准则。

• 【复旦】神经网络中的激活函数举例，它们各自的特点，以及哪个激活函数效果更好，为什么

  • sigmoid： \(\sigma(x)=1/(1+e^{-x})\)；
    • 优：将数值压缩到 0 1，导数为 \(\sigma(x)(1-\sigma(x))\) 好算。
    • 劣：输出均值非0（0.5），梯度消失（Gradient vanishing）每次传过来的梯度都会乘上小于1的值，靠近输出的层 参数更新幅度大，而靠近输入的层 参数更新幅度小。
  • ReLU： max(0, x) REctified Linear Unit
    • 优：不饱和（梯度不会过小），计算量小
    • 劣：输出均值非0，Dead ReLU：某层输入< 0，相应的输出值为0，那么此时该层就会"死亡"，参数不会更新，而且不可逆转，神经元永远失效。
    • Leaky ReLU： ＞0, 1 | ＜0, 0.1。解决 Dead ReLU。
  • Tanh：
    • 优：输出均值为0，原点附近与 y = x 函数相近；
    • 劣：梯度消失（Gradient vanishing，但比 sigmoid 好），计算量大。
  • softmax（应该并不算）： ，将多分类的输出值 转换为 0~1 Σ=1 的概率分布。

• 【复旦】损失函数有哪些

  • MSE：欧距离不开根号 L2 loss；RMSE。
  • MAE：绝对值 L1 loss。
  • cross-entropy（分类）： \(L=−[y\log\hat y+(1−y)\log(1−\hat y)]\) ，
  • Hinge Loss（分类）：正确类别 要比 其他类别 大一个 margin。

• 【复旦】BP 的英文全称，原理

  • backward propagation。
  • 首先，ANN 是怎么训练的。目标函数 求导 导数方向向下走一小步 gradient descent。
  • 求导：\(y=f(x), \partial y/\partial t=\partial y/\partial x\cdot\partial x/\partial t\)

• 【复旦】解决过拟合的方法并具体说明

  • 过拟合：训练集上表现很好，测试集上表现很差。欠拟合：训练集上表现很差。
  • 解决过拟合：
    • 通过交叉检验，得到较优的模型参数；
    • 正则化，loss 添加正则项。L1（绝对值的和）L2（平方开根）正则。

• 【复旦】支持向量机怎么改进，改进算法有哪些，改进方向是什么

  • SVM：分类超平面跟两类数据的间隔要尽可能大（即远离两边数据）
  • 先将数据变成线性可分的，再构造出最优分类超平面；通过选择一个核函数 K ，将低维非线性数据映射到高维空间中。
  • 优：
  • 劣：

• 【复旦】线性回归 / 逻辑回归，原理和区别

  • 线性回归：用 WT+b 直线 拟合数据，loss function MSE（欧几里得距离）。logistic 回归：sigmoid 函数套上一个回归模型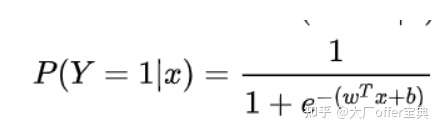， loss function 最大似然估计，多标签则 n 个 二分类器。
  • 逻辑回归：分类问题，线性回归：回归问题。
  • logistic 回归 损失函数：对数似然函数，\(L(\hat y,y)=-(y\log\hat y+(1-y)\log(1-\hat y))\)

• 【北航】朴素贝叶斯：

  • 全概率公式，贝叶斯公式 P(A|B) = P(B|A)*P(A)/P(B)。
  • p(类别|特征) = p(类别) Πp(特征|类别) / Πp(特征)
  • 朴素 naive：特征之间相互独立，无超参可以调。不朴素就是考虑特征间 相关 / 依赖关系。
  • 对异常值敏感吗？感觉不敏感，（比例不高的）异常值会被淹没。
  • 拉普拉斯修正：

• 【复旦】模式识别中有哪些常用距离（马氏距离、棋盘距离、街道距离、欧氏距离）

  • 欧氏距离：平方和开根号，旋转不变性。
  • 曼哈顿距离：|x1 - x2| + |y1 - y2|，城市街区距离。切比雪夫距离：max(|x1 - x2|, |y1 - y2|)
  • 马氏距离：两个分布有多相似，数据的协方差距离， 。
  • 余弦相似度：cos(A, B)＝ A*B / |A|*|B|，方向的差异。

• 特征归一化 / 标准化 / normalization：消除特征间 单位和尺度差异的影响。

• one-hot：把分类变量表示为二进制向量；直接使用不重复的数字，会将人工假设导致的误差引入到类别特征中。

• 【北航】处理高维组合特征，PCA：

  • 简化数据集的技术，它是一个线性变换，把数据变换到一个新的坐标系统中，任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上，依次类推。
  • 用于降维，同时保持数据集的对方差贡献最大的特征。

• 数据不平衡，如何解决：

  • 主要存在于有监督机器学习任务中。过多关注多数类，从而使得少数样本的分类性能下降。
  • 过采样 / 欠采样，改变权重，数据增强，集成学习（Adaboost），转换为异常检测问题。

• 【北航】决策树，随机森林：

  • 构造：
    • 学习一颗最优的决策树，是一个NP-完全问题，因此，传统决策树算法基于启发式算法，例如贪心 即每个节点创建最优决策。
    • 最优：最大 信息增益、信息增益比（解决数据不平衡）、Gini 系数。
    • 局部过拟合的剪枝：创建好决策树后，再从下往上剪枝。
  • 随机森林的随机性：每颗树的训练样本是随机的；选取的特征集是随机的。
  • 为什么不能用全样本 训练 m 棵决策树：因为训出来都一模一样，不能避免过拟合。
  • 优：随机森林并行，处理搞维度数据（不用降维）
  • 劣：训练慢，在噪声较大的数据集 过拟合。

• 【北航】集成学习：

  • Bagging：并行训练多个分类器，集体投票 减少方差。
  • Boosting：串行 迭代，提高被错误分类的样本的权重，降低被正确分类的样本的权重，集体投票。
  • XGBoost：

• （简历问题）ARIMA，LSTM，TCN，RNN：【】

  • ARIMA：
  • RNN：
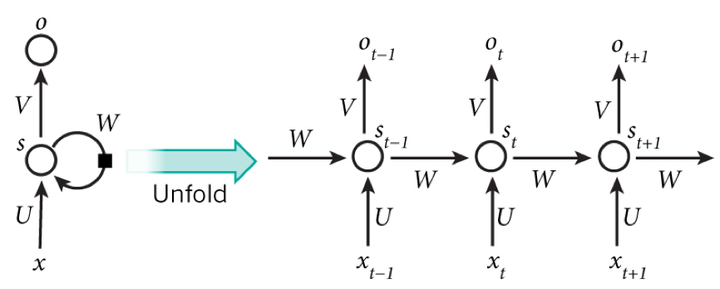
  • LSTM：RNN 的问题：不适用于长期记忆。基本思想：
    • 引入“门运算”，遗忘门 输入门，选择性记忆。
    • 引入“门运算”，将梯度中的累乘变为累加，解决梯度消失问题
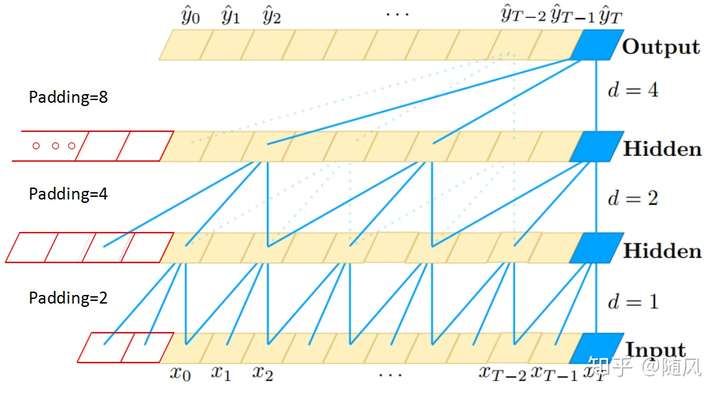
  • TCN：RNN 的问题：只能串行计算，要保存所有中间变量，因此非常计算密集。因果卷积 && 空洞 dilated 卷积 + 残差模块。
  • Markov：

• 【复旦】顶会或顶刊名称：

  • CVPR: International Conference on Computer Vision and Pattern Recognition；
  • ICCV: International Conference on Computer vision
  • ECCV: European Conference on Computer Vision
  • ICML: International Conference on Machine Learning
  • NeurIPS: Annual Conference on Neural lnformation Processing Systems
  • AAAl: Association for the Advancement of Artificial Intelligence
  • ICLR: International Conference on Learning Representation
  • IJCAI: International Joint Conferences on Artificial Intelligence
  • ACM SIGKDD: The Association for Computing Machinery's Special Interest Group on Knowledge Discovery and Data Mining
  • SIGGRAPH: Special Interest Group for Computer GRAPHICS
  • EMNLP: The Conference on Empirical Methods in Natural Language Processing
  • 顶刊：
    • TPAMl: IEEE Trans on Pattern Analysis and Machine Intelligence.
    • lJCV: International Journal of Computer Vision
    • TIP: IEEE Transactions on lmage Processing

操作系统（非重点）

• 【计算所】中断、虚拟内存、进程和线程通信

• 【北航】进程调度算法（可能是 LIFO 这种？）

  • FCFS 先到先得，SJF shortest job first 短作业优先，RR round-robin 轮流，multi level feedback queue

• 【北航】进程之间通信的方式：

  • shared memory，message passing。

• 【北航】进程和线程的区别：

  • 进程：资源分配最小单位，线程：资源调度最小单位
  • 进程有独立地址空间，代码段、堆栈段、数据段，线程共享进程中的数据，使用相同的地址空间。线程通信更方便，可以直接 shared memory。
  • 线程出错（段错误 除0），会 kill 掉整个进程（包括其他线程）

• 【北航】临界区：访问临界资源（互斥访问资源）的那段代码。

计算机网络（非重点）

• 【复旦】TCP 和 UDP 的区别

  • 

• 【北大】TCP 三次握手

  • 一次握手：客户端发送带有 SYN 标志的连接请求数据包给服务端
    二次握手：服务端发送带有 SYN+ACK 标志的连接请求和应答数据包给客户端
    三次握手：客户端发送带有 ACK 标志的应答数据包给服务端(可以携带数据了)
  • 四次挥手：两边都发 FIN+ACK。

• 【北航】输入网址点击转到后发生的事

  1. 应用层：DHCP 协议，得到本机 IP 地址。
  2. 网络层 / 链路层：ARP 协议，IP地址 → 物理地址，得到 DNS server 的 MAC 地址。
  3. 应用层 & 传输层 & 网络层 & 链路层：DNS 域名解析，得到 IP 地址
  4. 应用层 & 传输层 & 网络层 & 链路层：url 解析得到 HTTP 报文，组装 TCP/UDP → IP → MAC 报文，建立 TCP/UDP 连接。

• 【北航】计网 各个层的功能：

  • OSI：应用层，表示层，会话层，传输层，网络层，链路层，物理层。
  • TCP/IP：应用层，传输层，网络层，链路层，物理层。
  • 交换信息的表示方式，管理主机间的会话；
  • 传输层：为端到端连接提供（可靠的）传输服务。

• 【北航】为什么网络层不直接面向连接：

  • IP 地址不断变化，不断建立连接的代价。
  • 应用场景如视频通话，没有必要性。

• 【北航】DNS的工作原理：

  • 递归查询：本地 server 也不知道，那我去帮你问吧。
  • 迭代查询：本地 server 告诉你上一级 server 的地址，你再去问吧。

• 【北航】OSPF 协议：

  • open shortest path first。
  • 使用 link state 协议：发Hello报文 - 建立邻接关系 - 形成链路状态数据库 - dijkstra 算法 - 形成路由表。
  • 就是一个简单的寻最短路，链路cost是管理员配置的。
  • OSPF 消息直接承载在 IP 数据报中（而非TCP / UDP），有5种报文（hello DBD摘要 LSR详细讲讲 LSU我的状态多个LSA LSAck收到），不是ICMP通告。
  • OSPF属于哪一层：有些人说OSPF使用IP协议的功能，应该在IP层之上，即传输层；也有些人说OSPF是路由协议里的一种，应该属于网络层。OSPF报文直接封装在IP数据包内，专门为 TCP/IP 而设计的路由协议，因此属于网络层。

数据库（非重点）

• 【北航】1 2 3 NF 范式：
  • 1：数据表每一列都不可分割，即 某个数学不能有多个值，不能表中套表、
  • 2：每行必须可以唯一区分（主键存在）
  • 3：某个属性不依赖于其他属性。比如 AI工程师+金融 → 薪资=高，那么就单独建一张表存储这个关系。
• 【北航】除了关系型数据库还有什么数据库？
  • 网状数据库、层次数据库之类。

计算机组成原理（非重点）

• 【复旦】你电脑内存多少g的，硬盘多少g的，内存和硬盘的关系是怎样的

  • 16.0 GB (15.3 GB 可用)，512 GB，两码事，内存是硬盘的 cache。

• 【北航】设置缓冲区的理论依据：

  • 局部性原理：时间局部性（现在访问的 过会还可能访问）空间局部性（访问这个点 旁边数据也可能访问）。

• 【北大】【北航】电脑开机的过程：

  • 计算机是如何启动的，我说先进bios，老师打断我说bios在哪？我说rom啊，然后老师又问rom在哪，我猜是cpu（并不是），但不敢乱说，只好说没研究那么深。
  • 通电 → 初始化启动程序 BIOS → 操作权交给 CPU 载入 os 到内存。
  • 通电 → BIOS 硬件初始化和检查 → 控制权交给主引导记录(MBR) → MBR找启动文件并读入内存 → 控制权给启动文件 载入操作系统
  • BIOS：一组固化到计算机内主板上一个ROM芯片上的程序，保存着计算机最重要的基本输入输出的程序（ROM）、开机后自检程序、系统自启动程序，其主要功能是为计算机提供最底层的、最直接的硬件设置和控制。
  • 主板：
    • 电路板，安装了 BIOS芯片、南北桥芯片、I/O控制芯片、键盘和面板控制开关接口、指示灯插接件、扩充插槽、直流电源供电接插件 等元件
    • 如果说CPU是电脑的心脏，那么主板就是血管和神经，有了主板，电脑的CPU才能控制硬盘、软驱等周边设备。
    • 北桥芯片：主板上离CPU最近的芯片，控制 CPU 内存 显卡 等高速设备。
    • 南桥芯片：负责I/O总线之间的通信，如PCI总线、USB、LAN、ATA、SATA、音频控制器、键盘控制器、实时时钟控制器、高级电源管理等。
  • 按下开机开关，电脑主板给电源发送启动信号，电源开始向主板、硬盘、光驱等设备供电。
  • 硬件设备通电后，电脑开始启动，首先，主板开始初始化启动程序，主板BIOS先检测所有硬件是否连接正常。
  • 确认连接的设备正常后，电脑开始真正启动，主板会再一次对某些部件进行一些检测，准备载入操作系统。
  • 所有检测完成后，主板将操作权交给了CPU，CPU按照预订的程序，开始从硬盘读取储存的信息，并加载在内存
  • 系统的加载是相当复杂的，内容繁多，首先，系统先加载操作系统所需的文件，然后检测所有的硬件，加载相应硬件的驱动程序加载完毕后进入欢迎界面。

• 【北航】USB 接鼠标 键盘有什么区别。

  • 不需要在bios中进行任何设置，插在计算机usb口上可以直接使用，热插拔。

• 【北航】计算机的存储介质：

  • 半导体：ROM RAM，磁盘 磁介质。

• 【北航】计算机 组成 体系结构 有什么区别？

  • 组成：实现， 存储器 处理器 数据类型 指令格式 这些。
  • 体系结构：概念性结构和功能特性，更 high-level。

• 【北航】什么是虚拟内存，转换，TLB：

  • 虚拟内存：

    • 每个程序拥有自己的地址空间，这个地址空间被分割成多个块，每一块称为一页 (Page, 4KB)。
    • 这些页被映射到物理内存，但不需要映射到连续的物理内存，也不需要所有页都必须在物理内存中。
    • 虚拟内存：物理内存扩充成更大的逻辑内存，从而让程序获得更多的可用内存。程序不用将地址空间中的每一页都映射到物理内存，也就是说，一个程序不需要全部调入内存就可以运行，这使得有限的内存运行大程序成为可能。

  • MMU：地址空间 → 物理内存，TLB： Translation Lookaside Buffer 页表缓冲区。

编译原理（非重点）

• 【北航】从代码到可执行程序的步骤：
  • 词法分析，语法分析，语义分析，中间代码生成，优化中间代码，生成代码，优化代码。
  • 词法 lexical 分析：识别单词类型是什么（int x = 3 → int, x, =, 3)
  • 语法 syntax 分析：int x = 3 符合语法规则吗，fit 哪一条语法规则。
  • 语义 semantic 分析：这个语法规则代表什么意思，我们为语法规则配上什么样的动作。
  • 预处理 → 编译 → 汇编（得到二进制文件） → 链接（对调用的库）
• 词法分析：
  • language：字符串集合，比如 L = {ω | ω∈(a,b)*} 。
  • grammar 文法：表达 language 构成规则的形式化方法。\(G=(V_N,V_T,S,P)\)，非终结符集，终结符集，文法开始符号，产生式。
  • re ↔ FA ↔ grammar。
  • NFA → DFA：二进制状态法，n state 的 NFA，变成DFA 最多可能有 2^n 个 state。
  • DFA → minimum DFA：集合划分法。把所有状态认为是一个集合，根据集合状态转移的分歧，切割集合。
• 【北航】语法分析：LL 分析法，LR 分析法：
  • LL：
  • 终结首符集 FIRST(a)：从某个短语可以推出的 所有句子 的首终结符。
  • 后随终结符集 FOLLOW(A)：·所有合法句型中，可能出现在 A 后方的终结符集合。
  • 构造 预测分析表。
  • LR：
  • 画状态转移自动机 → LR分析表。
  • LL 和 LR 的比较：
    • 自上而下 & 自下而上。
    • LL 写程序更简单，分析表更小；
    • LR 适用范围更广，能支持更多 CFG（上下文无关文法）。
  • LL 和 LR 的限制：
    • LL：比如 LL(1)，如果两个产生式 拥有相同的 first 集，那么分析表冲突，不能用 LL。
    • LR：一个状态里，出现 移进-规约冲突，或有两个以上不同的规约。
• 【北航】上下文无关文法 CFG 的特点：
  • 可以随意将 文法规则左边的非终结符 替换为 右边的终结符或非终结符，不用考虑 LHS 的上下文。

其他

• 【复旦】句柄是什么，句柄怎么用。（不对，这好像是问的编译原理）
  • 在程序设计中，句柄是一种特殊的智能指针，指获取另一个对象的方法（广义的指针）。
  • Windows 句柄 16 位无符号整数。
  • 和内存管理的虚拟地址（段 页式，页表 MMU 翻译）有关。
• 【北航】面向对象的三个性质：
  • 封装 集成 多态（重载 overload 重写 override）。
• 【北航】函数名，函数指针，函数的入口地址：
  • 函数名：c语言中，函数名就是一个函数指针。
  • 入口地址：函数时执行的第一条指令的地址，通过这个地址可以找到该函数。
  • 函数指针：指向入口地址，就可以通过该指针调用函数了。
• 【北航】数组名，数组首地址，数组指针：
  • 数组名不是指针，是数组首地址。但 sizeof 时返回整个数组地址大小。
  • 编译器会自动将 数组名 a 替换为 指向该数组首元素的指针 &a[0]。
• malloc 和 new 的区别。
  • new从自由存储区上分配内存，malloc从堆上分配内存。自由存储区是C++基于new操作符的一个抽象概念，凡是通过new操作符进行内存申请，该内存即为自由存储区。
  • new、delete 返回的是某种数据类型指针；malloc、free 返回的是 void 指针。
  • 使用new操作符申请内存分配时，无须指定内存块的大小，编译器会根据类型信息自行计算；使用malloc则需要显式指出所需内存的尺寸。
  • new 可以调用对象的构造函数，对应的 delete 调用相应的析构函数；malloc 仅仅分配内存，free 仅仅回收内存，并不执行构造和析构函数。
  • new、delete 是操作符，可以重载；malloc、free 是函数，可以重写(覆盖)。