线性代数 | 最小二乘法的直观理解


两分钟理解最小二乘法！

最小二乘法的使用场景

在线性方程组 \(Ax=b\) 无解时，用最小二乘法来求近似解。

最小二乘法的公式

\(A^TAx=A^Tb\) 的解 \(x'\)（这个方程组一定有解），即为最小二乘法的近似解。

直观理解

直观上，\(Ax=b\) 有解 \(\iff\) b 落在 A 的列向量组成的超平面上。求解 \(Ax=b\)，就是求一组线性组合的系数 x，使得 A 的列向量的线性组合，正好落在 b 的位置。

反之，\(Ax=b\) 无解 \(\iff\) b 不落在 A 列向量的超平面上。此时，在 A 超平面上寻找离 b 最近的点，是一个求近似解的思路。

如图所示，假设 P 点代表 b 的位置，我们就要寻找 O 点，使得 PO 连线垂直于超平面 A，作为近似解 \(x’\)。

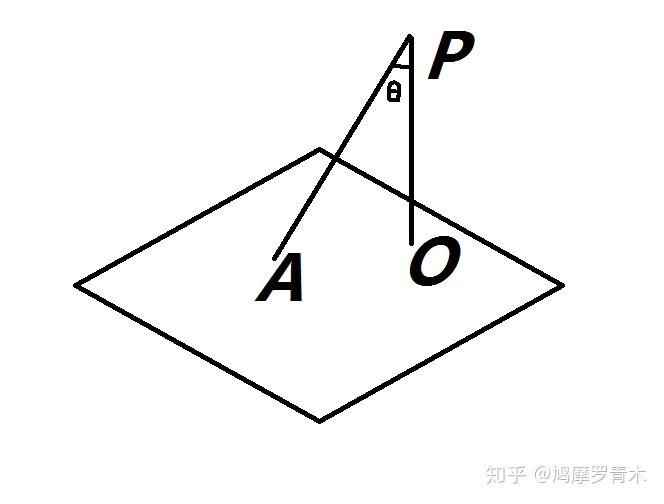
preview

O 点坐标为 \(Ax'\)，P 点坐标为 \(b\)，所以向量 PO 为两个坐标相减（\(Ax'-b\)）。我们希望这个向量垂直于超平面 A，也就是说，垂直于组成超平面的所有列向量，即 A 的所有列向量。

两个向量 \(d_1,d_2\) 相互垂直（向量正交）\(\iff\) 内积为零；用向量转置相乘计算内积，即 \(d_1^Td_2=0\)。所以，\(Ax'-b\) 垂直于 A 的所有列向量，可以写为 \(A^T(Ax'-b)=\vec0\)，也就是 \(A^TAx'=A^Tb\)。

你学会了嘛？😉

本站其他相关博客：



posted @ 2022-09-13 15:04  MoonOut  阅读(743)  评论(0)  编辑  收藏  举报