数据结构C++版
数据结构C++版
标签(空格分隔): 数据结构
第一章 绪论
一. 复杂度度量
-
时间复杂度:T(n)
(1)算法执行时间的变化趋势,可以表现为输入规模的一个函数,记为T(n),其中n是问题规模
(2)其实,T(n)的表示并不严谨,因为即使输入规模大小相同,输入的内容不同也会造成算法计算时间不同。例如:由n个元素组成的序列由\(n!\)种,有时所有元素都需交换,有时无需任何交换。所以,我们做一次简化,选择执行时间最长的输入规模作为T(n),并以T(n)作为度量该算法的复杂度。 -
渐进复杂度:O(f(n))
(1)对于同一问题规模的两个算法A和B,通过比较其时间复杂度\(T_A(n)和T_B(n)\),即可判定二者优劣 (带入n计算两个函数值比较大小)。但这并不是说明,对于所有问题规模,二者优劣总是一定的,因为有的算法适合小规模输入,有些则恰恰相反。
(2)我们总是关注大规模输入下的算法执行时间,因为小规模输入本身执行时间就很短。为了描述这种随着问题规模不断扩大带来的算法执行时间变化趋势,基于保守估计的原则,我们首先关注\(T(n)\)的上界,引入符号\(O\)
(3)具体的,若存在正常数c和\(f(n)\),使得任意 \(n>>2\) 都有:$$T(n) <= c*f(n)$$ 则可认为n足够大之后\(f(n)\)给出了\(T(n)\)的渐进上界,记为$$T(n) = O(f(n))$$
(4)所以对于 \(O\),有如下性质:
对任意 \(c>0\),有 \(O(f(n)) = O(c*f(n))\)
对任意常数 \(a>b>0\),有 \(O(n^a+n^b) = O(n^a)\) -
最好复杂度估计
(1)对算法执行时间的乐观估计,我们引入符号 \(\Omega\)
(2)若对于 \(n>>2\),都有 \(T(n) >= c*g(n)\),则可认为,在n足够大后,\(g(n)\) 给出了 \(T(n)\)的一个渐进下界,记为 $$T(n) = \Omega(g(n))$$ -
精确估计
(1)从渐进趋势来看,\(T(n)\)介于 \(\Omega(g(n))\)与 \(O(f(n))\)之间,若恰巧出现 \(g(n)=f(n)\),则可用 \(\Theta\) 符号来表示
(2)若对于正常数\(c_1,c_2\) 和函数 \(h(n)\),对于所有n>>2,都有$$c_1h(n) <= T(n) <= c_2h(n)$$
则可认为,n足够大之后,\(h(n)\) 给出了 \(T(n)\) 的一个确界,我们记为:$$T(n) = \Theta(h(n))$$
二. 递归
- 线性递归
(1)数组求和的线性递归版本:int sum(int A[],int n){ if (n<1) // 平凡情况,递归基 return 0; else return A[n-1] + sum(A,n-1); // 一般情况 } int main(){ int A[] = {1,2,34}; int res = sum(A,3); cout << "sum:" << res; // 37 }
(2)线性递归
a ) 算法sum()总是朝着更深层次进行自我调用,且每个实例对自身调用至多一次,使得这些调用形成线性关系。
b ) 线性递归的解分为两步:第一对应于单独的某个元素,可直接求解。另一个对应于剩余部分,其结构与原问题相同(eg: A[n-1]),子问题的解经过简单合并后即可得到原问题的解。
(3)减而治之:线性递归每深入一层,带求解问题的规模都缩减一个常数,直至最终化为平凡小问题。
-
递归分析sum函数
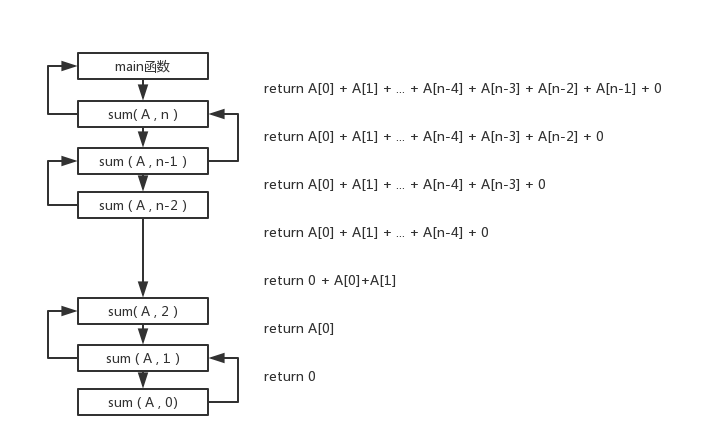
(1)递归跟踪:用分析递归算法的总体运行时间与空间,将递归算法执行过程整理为图的形式。
![digui1.png-24.9kB]()
每一个递归实例中所涉及的非递归部分分为三类(判断n是否为0,累加sum(n-1)+A[n-1],返回当前总和),共需计算时间为常数\(O\)(3)。
对于长度为n的输入数组,递归深度应为n+1,故整个sum算法的运行时间为 $ (n+1) * O$(3) = \(O\)(n)
(2)递归方程 -
递归模式
(1)多递归基:
为保证有穷性,递归算法都应设置递归基,且应针对可能出现的平凡情况,都需设置递归基,故同一个递归基可能不止一个。
线性递归实现数组反转:void reverse(int* A,int low, int high){ if(low < high){ swap(A[low],A[high]); reverse(A,low+1,high-1); } } int main(){ int A[] = {23,45,12,57,28}; reverse(A,0,4); for(int i=0;i<sizeof(A)/sizeof(A[0]);i++) cout << A[i] << "," ; }
(2)多项递归
递归算法中,不止递归基有多个,递归调用也可能有多个不同的分支选择。虽然选择多,但是之中从中选择一个递归分支,因此,这种方式仍属于线性递归。
-
递归消除
(1)空间成本
(2)尾递归及其消除
若递归调用在递归实例中恰好以最后一步的形式出现,则这个递归是尾递归。尾递归消除可以用goto语句和while循环消除// goto消除尾递归 void reverse_goto(int* A,int low, int high){ next: if(low < high){ swap(A[low++],A[high--]); goto next; } } // while消除尾递归 void reverse_while(int* A,int low, int high){ while(low < high) swap(A[low++],A[high--]); } -
二分递归
(1)分而治之:
分而治之就是将问题分解为若干规模更小的子问题,再通过递归机制分别求解。这种分解持续进行,直到子问题规模缩减至平凡情况。(divide-and-conquer)策略。
通常把问题一分为二,故称做二分递归。无论是分解2个还是更大常数个子问题,对算法总体的渐进复杂度并无实质影响。
直观来讲,二分递归就是算法的最后一句,2次递归调用的组合。
(2)二分递归下的数组求和
二分递归的每个递归实例都可向下递归两次,所以二分递归下的递归基出现的相当频繁,会有超过半数的递归实例都是递归基。int sum(int A[],int low,int high){ if( low==high ) return A[low]; int mid = (low + high) >> 1; // 除2向下取整 return sum(A,low,mid) + sum(A,mid+1,high); // 两次递归调用 } int main() { int A[] = {1,2,3,4,5,6,7,8}; int i = sum(A, 0, 7); cout << i; }
(3)效率
二分递归的计算消耗来自两方面:子问题划分和子问题解答的合并。为使分治策略真正有效,划分出的子问题需要可独立求解,而无需其他子问题的原始数据或中间结果。
(4)Fibnoacci数:二分递归
```c
int fib(int n){
if (n<2)
return n;
else
return fib(n-1) + fib(n-2);
}
int main() {
int i = fib(3); // 斐波那契数列:0,1,1,2,3,5
cout << i;
}
```
(5)优化策略
上述二分递归计算斐波那契的做法,并没有充分体现分治的思想,因为子问题之间会相互引用各自的数据。eg:fib(n)=fib(n-1)+fib(n-2)的划分问题,但是fib(n-1)需要再递归一次fib(n-2)的结果。为了消除这种重复递归,一种自然的思路就是:借助一定的辅助空间,在各自问题求解后,及时记录下其对应的解答
这种方式就形成了两种做法:一种是从递归基出发,自底向上递推得出各子问题的解,这是所谓的动态规划。另一种是通过直接调阅记录获得解答,从而避免从新计算。这就是所谓的查表法。
(6)Fibonacci数:查表法 -> 线性递归
思路:递归基种要有保存上一项的参数.使得每一个字问题的解答只会调用一次。在该算法抵达递归基之后的逐层返回过程中,每向上返回一层,以下各层的解答均不需继续保留。
```c
int fib(int n,int& pre){ // pre:引用
if (n==0) {
pre = 1;
return n;
}
else{
int pre2 ;
pre = fib(n-1,pre2);
return pre2+pre;
}
}
int main() {
int fak = 100;
int i = fib(3,fak); // 斐波那契数列:0,1,1,2,3,5
cout << i;
}
```
(7)Fibonacci数:动态规划=>迭代
思路:动态规划先从最小的子问题开始,设f(0)=0,f(1)=1,开始逐个循环
```c
int fib(int n){
int a = 0; // f(0)
int b = 1; // f(1)
while(n>0){
int tmp = b;
b = a+b;
a = tmp;
n--;
}
}
int main() {
int fak = 100;
int i = fib(4); // 斐波那契数列:0,1,1,2,3,5
cout << i;
}
```
#include <cstdlib>
#include <iostream>
using namespace std;
typedef int Rank;
#define DEFAULT_CAPACITY 4
template <typename T> class Vector{
protected:
Rank _size; // 元素个数
int _capacity; // 内部数组大小
T* _elem; // 数据区
void copyFrom(T const* A,Rank lo,Rank high ){
_elem = new T[_capacity=2*(high-lo)];
while( lo<high ){
_elem[_size++] = A[lo++] ; // 复制到 _elem[0,high-lo)
}
}
/**
* 内部数组动态扩容算法:基于数组赋值
* (1)与原生数组相比,可扩充向量更加灵活,只要系统尚有空间可用,其规模不再受限于初始容量
* (2)每一次由n扩容到2n,都需要话费O(2n)=O(n)时间,这也是最坏情况下插入操作所需时间。表面来看,这一策略的效率很低,
* 但随着向量规模的不断扩大,在执行插入操作前需要进行扩容的概率也越来越低,所以,就平均意义而言,用于扩容的时间成本不至很高。、
* (3)分摊时间:如果连续对数组扩容,将其所有时间累积起来,分摊至每次操作。此处,我们可以连续对结构进行n次查询,插入,删除操作,计算下平均下来的分摊时间。
* 有意思的是,即便我们连续进行n次都是插入的操作,用于扩容的平均分摊时间也不过是O(1),定义如下函数:
* size(n) = 连续插入n个元素后响亮的规模
* capacity(n) = 连续插入n个元素后数组的容量
* T(n) = 连续插入n个元素而花费在扩容的时间
* 因为只有在数组装满的情况下才会扩容,所以数组的装填因子始终大于等于50%,所以会有size(n) <= capacity(n) <= 2*size(n),所以会有
* capacity(n) = O(size(n)) = O(n),又因为,每次扩容所需时间正比于当时的数组规模。同样以2倍的速度增长,
* 所以用于扩容的时间累积为T(n) = 2n + 4n + 8n +...+ capacity(n) < 2*capacity(n) = O(n)。将其平均分摊到n次操作中,相应时间为O(1)。
* 早期的数组扩容多采用追加固定数组单元,此类分摊时间高达O(n)
*/
void expand(){
if(_size < _capacity) // 尚未满员,不必扩容
return ;
if(_capacity<DEFAULT_CAPACITY)
_capacity = DEFAULT_CAPACITY; // 不低于最小容量
T* oldElem = _elem;
_elem = new T[_capacity <<= 1]; //容量加倍
for(int i=0;i<_size;i++)
_elem[i] = oldElem[i];
delete [] oldElem;
}
/**
* 缩容:装填因子不足25%时压缩所占空间
* 缩容的平均分摊时间也为O(1)
*/
void shrink(){
if(_capacity<DEFAULT_CAPACITY <<1) // 不至收缩到DEFAULT_CAPACITY以下
return;
if(_size <<2 > _capacity) // 以25%为界
return;
T* oldElem = _elem;
_elem = new T[_capacity >>= 1]; // 容量减半
for (int i = 0; i < _size; i++) {
_elem[i] = oldElem[i];
}
delete [] oldElem;
}
/**
* 置乱器:在软件测试,仿真模拟中,随机向量生成都是至关重要的操作
* @param V :可通过V[i]访问数据元素
*/
void permute(Vector<T> &V){
for (int i = 0; i < _size; i++) {
int a=1,b=2;
swap(V[i],V[rand()%(i+1)]);
}
}
public:
/**
* 构造函数
* @param c :容量。内部数组大小
* @param s :元素个数
* @param v :数组中的初始值
*/
Vector(int c=DEFAULT_CAPACITY,int s=0,int v=0){
_elem = new T[_capacity=c];
for(_size=0;_size<s;_size++){
_elem[_size] = v;
}
}
/**
* 析构函数:只需释放内部数组_elem[],_size和_capacity这种内部变量无须作任何处理,他们会随着对象的销毁备操作系统回收
*/
~Vector(){
delete[] _elem;
}
/**
* 重载操作符"="
* @param V : 赋值的vector
* @return
*/
Vector<T>& operator= (Vector<T> const& V){ // 默认运算符"="不足以支持向量间的直接赋值
if(_elem)
delete[] _elem; //释放原有内容
copyFrom(V._elem,0,V._size);
return *this;
}
/**
* 通过Vector[i]访问向量中的元素
*/
T& operator[](Rank r) const {
return _elem[r];
}
/**
* 无序向量查找:
* 自向量末元素起,向前找出元素e的位置。
* 此算法最坏情况下O(high-lo)=O(n),最好情况为O(1),对于规模相同,内部组成不同的输入,渐进运行时间有所差别,故称输入敏感算法。
* @param e :待查严肃
* @param lo :查找范围为[lo,high)
* @param high
* @return
*/
Rank find(T const& e,Rank lo,Rank high)const{ // assert: 0 <= lo < high <= _size
while( (lo<high--) && e!=_elem[high] ); // while(lo<high--)的顺序:先判断,再自减,再while
return high; // 跳出循环时,high = lo-1
}
/**
* 插入: 将e作为秩为r的元素插入
* 新插入元素越靠后,所需时间越短。平均插入时间为O(n)
* @param r :秩,前缀元素的个数,等于元素角标
* @param e
* @return
*/
Rank insert(Rank r,T const& e){
expand(); // 如有需要,进行扩容。
for (int i = _size; i > r; i--) {
_elem[i] = _elem[i-1];
}
_elem[r] = e;
_size++;
return r; // 返回秩
}
/**
* 删除:删除区间[lo,hi)的元素
* 删除单个元素可用 remove(r,r+1).最好O(1),最坏O(n)
* @param lo
* @param hi
* @return
*/
int remove(Rank lo,Rank hi){
if (lo == hi) // 处于效率原因,退化情况单独考虑
return 0;
while( hi<_size )
_elem[lo++] = _elem[hi++]; // 删除前,容器规模_size个
_size = lo; // 更新规模,丢弃尾部[lo,_size=hi]区间的元素
shrink(); // 如有必要,进行缩容
return hi-lo; // 返回被删除的元素数目
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号