数据结构（九）排序

第九章排序

9.1 基本概念

排序是线性表的一种操作
每个元素叫做记录，输入是一个元素集合，输出是一个元素集合
内排序吧整个数据ui放在内存中进行排序，外排序由于记录个数太多，不能全部放在内存中
7种排序算法分为两大类：
（1）简单算法：冒泡排序，简单选择排序，直接插入排序
（2）改进算法：希尔排序，堆排序，归并排序，快速排序

排序用到的数据结构
（1）线性表
（2）数组元素交换操作

#include <stdio.h>
#define MAXSIZE 10
typedef struct{
    int r[MAXSIZE+1] ;   // r[0]用于存储哨兵或临时变量
    int length;
}SqList;

void swap(SqList *l,int i,int j){
    int temp = l->r[i];
    l -> r[i]  = l->r[j];
    l->r[j] = temp;
}

（3）数组打印
c void printSqlList(SqList *l){ for (int i = 0; i < l-> length+1; i++) { printf("%d , ",l-> r[i]); } }

9.2 冒泡排序

冒泡排序的基本思想：
两两比较相邻记录的关键字，如果反序则交换记录，直到没有反序为止。
算法实现：
（1）冒泡排序每次循环都把一个最小的元素放到无序表的最顶端
（2）这个比较要从线性表的最后一位开始，逐个比较，把小的交换到前面，不断比较到线性表的开头，此时，最小的元素被放到了最开始的位置。
（3）当发现某一次循环中，未发生元素交换，就是说每个相邻元素，都是左小右大的，此时，线性表已经全具有序，不需要再次比较。引入flag比较为
```
/* 冒泡排序 */
void bubbleSort(SqList *list){
  int flag = 1;
   for (int i = 1; i < list->length  && flag ; i++) {    // 数组0位置不是元素
      flag = 0;
       for (int j = list->length-1; j >= i; j--) {
           if(list->r[j+1] < list->r[j]){
               flag = 1;    // 产生交换操作，下一次还需要进行比较交换
               swap(list,j,j+1);
           }
       }
   }
}
```

（4）冒泡排序的时间复杂度
最好情况：线性表已经有序，需要比较n-1次
最坏情况：比较次数(n-1) + (n-2) + (n-3)+ ... +3 + 2 + 1 = \(\frac{n(n-1)}{2}\)
所以总时间复杂度：O(n^2)

9.3 简单选择排序

冒泡排序不停的进行比较和交换，确保局部为左小右大。而简单选择排序，是一种不断进行比较，却很少次数交换的排序算法
简单选择排序：选择无序列表中最小的元素，用一个min标记记录该元素位置。然后把该元素和无序列表的第一个元素交换
简单选择排序的时间复杂度
所有的比较次数：最后一趟比较1次，倒数第二趟比较2次，所以一共比较1+2+3+..+(n-1)=\(\frac{n(n-1)}{2}\)
最好的时候，交换次数为0，最坏的情况下，交换次数为O(n),所以比较次数+交换次数形成算法的时间复杂度O(\(n^2\))，
```
/* 简单选择排序 */
void simpleSelest(SqList *list){
   for (int i = 1; i < list->length; i++) {
       for (int j = i+1; j <= list->length; j++) {
           int min = i;
           if(list->r[min]>list->r[j])
               min = j;
           if(min != i)
               swap(list,i,min);
       }
   }
}
```

9.4 直接插入排序

直接插入排序的思想
（1）直接插入排序是把无序列表中的每个元素，插入到已经排好序的有序列表中
（2）角标为0的位置，存放每次待插入的元素值。
时间复杂度
直接插入排序的时间复杂度要好于冒泡排序和简单选择排序，他的平均比较和移动次数约为\(\frac{n^2}{4}\)

算法

/* 直接插入排序 */
void insertSort(SqList *list){
    for (int i = 2; i <= list->length ; i++) {  // 初始情况下，认为第一个数据是有序列表
        if(list->r[i] < list->r[i-1]){
            list->r[0] = list->r[i];    // 哨兵
            int j;
            for (j = i-1;  list->r[j] > list->r[0]  ; j--) {  // 从插入元素向前查，找到需要插入的位置
                list->r[j+1] = list->r[j];
            }
            list->r[j+1] = list->r[0];
        }
        printSqlList(list);
        printf("\n");
    }
}

9.5 希尔排序

冒泡排序，简单选择排序，直接插入排序一个比一个节省时间。但是都没有突破O(\(n^2\))的限制。长期以来，算法界甚至觉得一切排序算法都无法超越O(\(n^2\))。
直到希尔排序出现，把时间复杂度提高到O(n*logn)。之后出现了一批超越O(\(n^2\))的算法
直接插入排序在某些情况下的效率很高：比如记录本身基本有序，只需少量插入操作就可以完成排序。还有就是纪录很少，插入的次数也就不多。但是这两个条件很苛刻。所以希尔排序出现了
。他的思路就是把无序列表，向着记录数少，基本有序靠拢。
希尔排序不是稳定的排序

希尔排序的思想：
希尔排序是分组内的直接插入排序。每趟保证分组内有序，最后increment为1，进行一次全部的直接插入排序

/* 希尔排序 */
void shellSort(SqList *list){
    int increament = list->length ;
    do{
        increament = increament/3 + 1;     // 增量序列
        printf("increament is %d :",increament);
        for (int i = increament+1; i <= list->length ; i++) {
            if(list->r[i] < list->r[i-increament]){   //  初始时r[1]与r[increment]比较
                list->r[0] = list->r[i];            // 暂存
                int j = 0;
                // 下面的形式就是直接插入排序的代码，但是希尔时分组的，所以比较后的移位移动increment位
                for (j = i-increament; j>0 && list->r[0] < list->r[j] ; j-=increament) {
                    list->r[j+increament] = list->r[j];
                }
                list->r[j+increament] = list->r[0];
            }
        }
        printSqlList(list);
    }while (increament > 1);
}

9.6 堆排序

概念
（1）堆排序是对简单选择排序的一种改进，简单选择排序在待排序的n个记录中选择一个最小记录需要比较n-1次。可是这种操作没有把每一趟的比较结果保存。而堆排序，改进了这种情况
（2）节点大于等于左右孩子结点的完全二叉树称为大顶堆
节点小于等于左右孩子节点的完全二叉树称为小顶堆

堆排序的思想：
（1）将待排序的序列形成大顶堆，使得根节点为待排数中最大的数
（2）将这个堆顶根节点和堆数组末尾的元素交换，使得堆数组的末尾元素为最大值，然后再将前面的n-1个结点序列重新构成一个堆，这样就能得到次小值。如此反复，得到一个有序序列。

#include <stdio.h>
#define MAXSIZE 20
typedef int ElementType;
typedef struct {           // 定义线性表
    ElementType Data[MAXSIZE];
    int length;
}SqList;

int getElem(SqList list,int i,ElementType *e){
    if(list.length ==0 || i <1 || i>list.length)
        return 0;
    *e = list.Data[i];
    return 1;    // 1代表成功
}

int insertList(SqList *list,int i, ElementType e){
    if (list->length == MAXSIZE || i<1 || i>list->length+1 )
        return 0;
    // 插入数据时将被查位置后的元素向后移1位,如果是在最后一位操作，则不用这个操作
    if(i <= list->length){
        for(int j=list->length-1;j>i-1;j--){
            list->Data[j+1] = list->Data[j];
        }
    }
    list->Data[i-1] = e; // 线性表角标=数组角标+1
    list->length++;
    return 0;
}

void HeapAdjust(SqList *list,int s,int m){
    int temp ;
    temp = list->Data[s];
    printf("tmp is : %d\n",temp);
    for (int i = 2*s; i <= m ; i *= 2) {
        if(i<m && list->Data[i]<list->Data[i+1])
            ++i;   // i是关键字中较大的记录下标
        if(temp >= list->Data[i])
            break;
        list->Data[s] = list->Data[i];
        s = i;
    }
    list->Data[s] = temp;
}
/* 堆排序 */
void heapSort(SqList *list){
    int i;
    for (int i = list->length/2; i > 0 ; i--) {
        HeapAdjust(list,i,list->length);
    }
    for (int i = list->length; i > 1 ; i--) {
        int temp = list->Data[i];
        list->Data[i] = list->Data[1];
        list->Data[1] = temp;
        HeapAdjust(list,1,i-1);
    }
}

int main(){
    printf("start\n");
    SqList list = {{999,13,25,3,99,41},5};
    SqList *l = &list;
    heapSort(l);
    for (int i = 0; i < 6; ++i) {
        printf( "%d, ",list.Data[i]);
    }
}

9.7 快速排序

对冒泡排序的改进
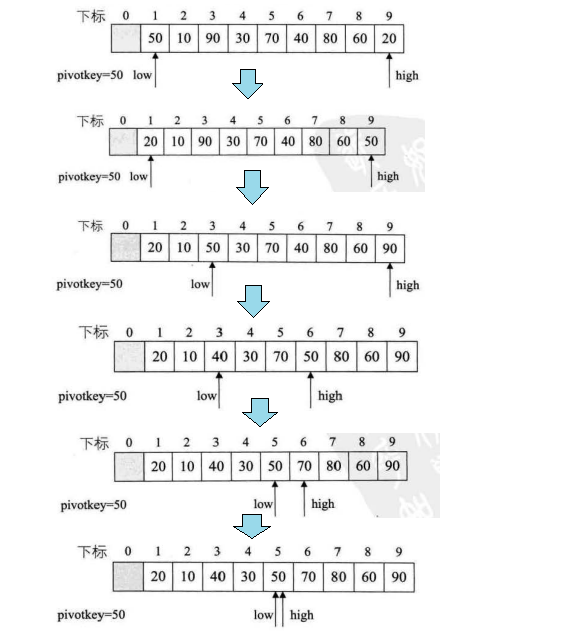
它每次选取一个枢轴，让枢轴左边的数都比枢轴小，枢轴右边的数都比枢轴大。
排序过程

代码实现

#define MAXSIZE 10
typedef struct{
    int r[MAXSIZE+1] ;   // r[0]用于存储哨兵或临时变量
    int length;
}SqList;

void qsort(SqList *L,int low ,int high);
int partition(SqList *L,int low,int high);
void quickSort(SqList *L){
    qsort(L,1,L->length);
}
void qsort(SqList *L,int low ,int high){            /* 递归调用，对枢轴左边和右边分别递归 */
    int pivot;                                      /* 枢轴 */
    if(low < high){
        pivot = partition(L,low,high);              /* 调整枢轴到正确的位置 */
        qsort(L,low,pivot-1);
        qsort(L,pivot+1,high);
    }
}
int partition(SqList *L,int low,int high){
    printf("low:%d，high:%d\n",low,high);
    int pivotkey;
    pivotkey = L->r[low];
    while(low<high){
        while(low<high && L->r[high] >= pivotkey)    /* 找到右侧比pivot数小的 */
            high--;
        swap(L,low,high);

        while(low<high && L->r[low] <= pivotkey)      /* 找到左侧比pivot数大的 */
            low++;
        swap(L,low,high);
    }
    return low;                                       /* 跳出while时，low=high=枢轴位置 */
}
/*********
 测试代码
 *********/
int main(){
    SqList list = {{-100,13,25,3,12,8,67,99,41,33,24},10};
    SqList *l = &list;
    quickSort(l);
    for (int i = 1; i < 10; ++i) {
        printf( "%d, ",list.r[i]);
    }
}

posted @ 2016-10-08 12:03 moon_lord 阅读(818) 评论(0) 编辑收藏举报

刷新页面返回顶部

moon_lord