数据结构(七)图
第七章 图
7.1 概念
- 连通图:如果图中任意两点都有路径,则该图是连通图
- 若一个有向图恰有一个顶点的入度为0,其与定点入度为1,则是一颗有向树
7.2 图的物理存储结构
因为图的节点度数相差很大,按照度数最大的顶点设计节点结构会造成存储单元浪费;如果按照每个顶点自己的度数设计不同结构,又会带来操作的不便
一、邻接矩阵
-
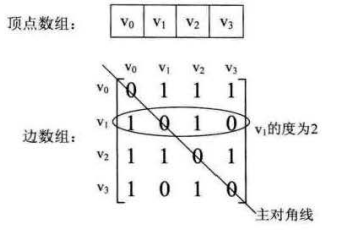
邻接矩阵存储使用2个数组存储图的信息:1个以为数组存储顶点,一个二维数组存储边的信息
(1)二维数组中的对角线为0,以为不存在顶点到自身的边
(2)要知道某个点的出度,就是顶点vi在第i行的元素之和,入度就是该顶点所在列的元素之和
(3)顶点vi的所有邻接点就是吧矩阵中第i行元素扫描一遍
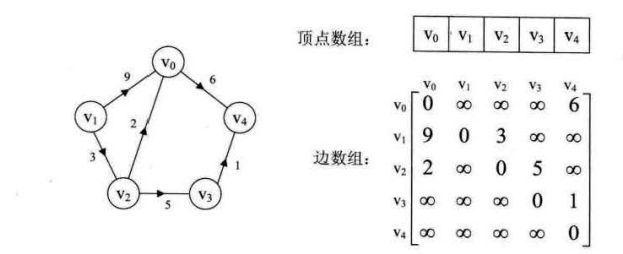
(4)对于有权值的网,二维数组中的元素不再是0,1表示是否存在边,而是把元素值表示为权值。不存在的边,权值记录为\(\infty\);对角线上的权值为0.
-
邻接矩阵定义图
#include <stdio.h> typedef char VertexType; typedef int EdgeType; #define MAXVEX 100 #define IUNFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表*/ EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵 */ int vnum,edgenum; /*定点的个数和边的个数*/ }MGraphy; void createGraphy(MGraphy *g){ printf("input vetex num and edge num\n"); scanf("%d,%d",&g->vnum,&g->edgenum); for (int i = 0; i < g->vnum ; i++) { // 输入顶点字符 printf("input %d vetex:",(i+1)); setbuf(stdin, NULL); scanf("%c",&g->vexs[i]); } for(int i=0;i<g->vnum;i++){ // 初始化数组元素 Infonity for(int j=0;j<g->vnum;j++){ g->arc[i][j] = IUNFINITY; } } printf("input a,b,c represent corner mark and weight\n"); for(int i=0;i<g->edgenum;i++){ int a,b,c=0; printf("%d edge:",(i+1)); setbuf(stdin,NULL); scanf("%d,%d,%d",&a,&b,&c); g->arc[a][b] = c; g->arc[b][a] = c; // 无向图增加这个 } } int main() { MGraphy g ; createGraphy(&g); }
二. 邻接表
-
邻接矩阵对于顶点多而边数少的稀疏图造成存储空间的大量浪费。正如线性表的预先分配可能造成存储空间浪费,因此引入链式存储结构。同样可以考虑用链表存储边或弧。
-
邻接表:数组 + 链表
(1)用的数组存储每个节点
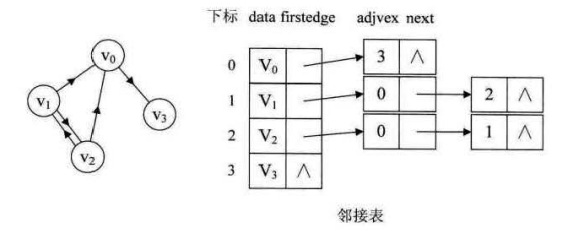
(2)数组中的每个节点的所有邻接点组成一个链表(因为邻接点的个数不确定)。这个邻接表就是顶点的出度表
(3)邻接表的图形表示
(4)邻接表关心了出度,但是查找入度就需要遍历整个图 -
创建邻接表
#include <stdio.h> #include <malloc.h> typedef char VertexType; typedef int EdgeType; #define MAXVEX 100 #define IUNFINITY 65535 typedef struct EdgeNode{ int adjvex; /* 邻接点域,该顶点对应的下标 */ EdgeType weight; EdgeNode *next; /* 链,指向下一个邻接点 */ }EdgeNode; typedef struct VertexNode{ /* 顶点表结点 */ VertexType data; /* 节点名字 */ EdgeNode *firstedge; /* 边表头节点 */ }VertexNode; typedef struct{ VertexNode adjList[MAXVEX]; /* 顶点表是一个结构体数组,数组中的元素是Vertex节点 */ int vnum,enumber; /* 图中当前顶点和边数 */ }GraphyAdjList; /* 建立邻接表结构 */ void createGraphy(GraphyAdjList *g){ EdgeNode *e; printf("input vertexNum and edgeNum:\n"); setbuf(stdin,NULL); scanf("%d,%d",&g->vnum,&g->enumber); for (int i = 0; i < g->vnum; i++) { printf("int %d vertex",(i+1)); setbuf(stdin,NULL); scanf("%c",&g->adjList[i].data); g->adjList[i].firstedge = NULL; /* 将边表设为空 */ } /* 建立边表 */ for (int k = 0; k < g->enumber; k++) { printf("input edge serialize num (i,j):\n"); int i,j; setbuf(stdin,NULL); scanf("%d,%d",&i,&j); e = (EdgeNode *) malloc (sizeof(EdgeNode)); } }
7.3 图的遍历
一. 基本思路
-
图的遍历:从图中某一个顶点出发遍历途中其余顶点,每一个顶点仅被访问一次
-
基本思路
(1)树有四种遍历方式,因为根节点只有一个。而图的复杂情况是的顺着一个点向下寻找,极有可能最后又找到自己,形成回路导致死循环。
(2)所以要设置一个数组voisited[n],n是图中顶点个数,初值为0,当该顶点被遍历后,修改数组元素的值为1
(3)基于此,形成了2中遍历方案:深度优先遍历和广度优先遍历
二. 深度优先遍历(DFS)
-
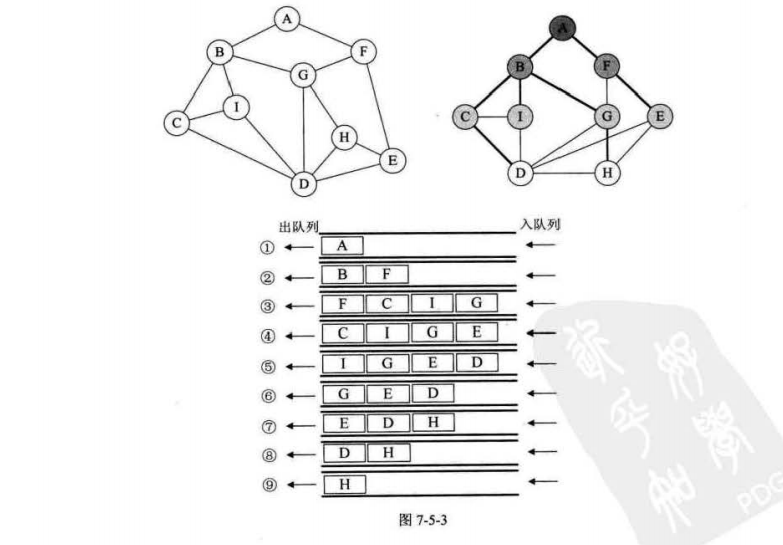
如下图所示,我们进行深度遍历,一个原则就是,每当我们发现有多个出度时,选择右手边的出度作为下一个遍历的顶点路径。
(1)从A出发,发现出度为B,F。选择右手边的B。A->B
(2)从B出发,出度为C,I,G,选择右手边的C
(3)从C出发,出度为I,D,选择右手边的D
(4)从D出发,出度为I,G,H,E,选择右手边的E
(5)从E出发,出度为H,F,选择右手边的F
(6)从F出发,出度为A,G,选择右手边的A,但发现A已经被遍历过,所以选择G
(7)从G出发,出度为B,D,H,B,D访问过了,选择H
(8)从H出发,出度为D,F,均被访问过了。但此时图中的节点并没有遍历完全,因此我们要按原路返回,去找没走过的路
(9)回退到G,发现所连接的BDFH均被访问;
(10)回退到F,没有通道;回退到E,没有通道,回退到D,发现一个点I,进行标记(若此时与D相邻的还有其他顶点,则在此时一起进行标记);然后继续回退到A,走完整个路 -
邻接矩阵下的深度遍历
int visited[MAXVEX] = {0}; void DFS(MGraphy g,int i){ visited[i] = 1; printf("%c,\t",g.vexs[i]); for (int j = 0; j < g.vnum; j++) { if(g.arc[i][j]!=0 && g.arc[i][j]!=IUNFINITY && !visited[j]){ DFS(g,j); } } } void DFSTraverse(MGraphy g){ printf("deep first search begin.\n"); for (int i = 0; i < g.vnum; i++) { if(!visited[i]){ DFS(g,i); } } } int main() { MGraphy g ; createGraphy(&g); printf("graphy create success ! ! !\n"); DFSTraverse(g); } -
邻接表下的深度遍历
int visited[MAXVEX] = {0}; void DFS(Graph g, int i){ printf("%c",g.vset[i].name); visited[i] = 1; EdgeNode *edgeNode = g.vset[i].firstedgeNode; while(edgeNode!=NULL){ if(!visited[edgeNode->index]) DFS(g,edgeNode->index); edgeNode = edgeNode->next; } } void DFStraverse(Graph g){ for (int i = 0; i < g.vNum; i++) { // 用于不同连通分量 if(!visited[i]) DFS(g,i); } } int main() { Graph g; createGraphy(&g); printf("create graphy success ! ! !\n"); DFStraverse(g); }
三. 广度优先遍历
-
广度优先遍历类似输的层次遍历
(1)先入队列一个元素
(2)弹出队列顶端的1个元素打印,并把它连接的顶点入队
(3)重复以上过程,直到队列为空 -
BFS的过程
-
BFS的实现
(1)邻接矩阵的BFStypedef char VertexType; typedef int EdgeType; #define MAXVEX 100 #define IUNFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表*/ EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵 */ int vnum,edgenum; /*定点的个数和边的个数*/ }MGraphy; /** * 邻接矩阵遍历图 * @param g */ void BFSTraverse(MGraphy g){ SeqQueue *queue; initQueue(queue); // 顺序表实现的队列,先初始化 int visited[] = {0}; // 初始化每个结点对应为未访问 int a; for(int i=0;i<g.vnum;i++){ // 对每个结点进行深度遍历 if(visited[i] == 0){ visited[i] = 1; printf("%c",g.vexs[i]); // 深度遍历后对结点进行打印操作 enQueue(queue,i); // 将节点放到队列中 while (queueLength(queue)){ deQueue(queue,&a); // 取出对头元素,进行广度遍历 for (int j = 0; j < g.vnum; ++j) { if(g.arc[a][j] == 1 && visited[j]==0){ // 存在边,且对应的店没有方问过 visited[j] = 1; printf("%c",g.vexs[j]); enQueue(queue,j); // 遍历后再入队 } } } } } }
(2)邻接表的BFS
```c
typedef char VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define IUNFINITY 65535
typedef struct EdgeNode{
int adjvex; /* 邻接点域,该顶点对应的下标 */
EdgeType weight;
EdgeNode *next; /* 链,指向下一个邻接点 */
}EdgeNode;
typedef struct VertexNode{ /* 顶点表结点 */
VertexType data; /* 节点名字 */
EdgeNode *firstedge; /* 边表头节点 */
}VertexNode;
typedef struct{
VertexNode adjList[MAXVEX]; /* 顶点表是一个结构体数组,数组中的元素是Vertex节点 */
int vnum,enumber; /* 图中当前顶点和边数 */
}GraphyAdjList;
/**
* 广度优先遍历邻接表
* @param g
*/
void BFSTraverse2(GraphyAdjList *g){
SeqQueue *queue;
initQueue(queue);
int a;
int visited[g->vnum] = {0};
for (int i = 0; i < g->vnum; ++i) {
if(visited[i] == 0){
visited[i] = 1;
printf("%c",g->adjList[i].data); // 打印定点
enQueue(queue,i);
while(queueLength(queue)!=0){
deQueue(queue,&a);
EdgeNode *p = g->adjList[i].firstedge; // 进入结点的邻接表
while (p!=NULL){
if(visited[p->adjvex] != 0){
visited[p->adjvex] == 1;
printf("%c\n",g->adjList[p->adjvex].data);
enQueue(queue,p->adjvex);
}
p = p->next;
}
}
}
}
}
```
7.4 最小生成树
- 应用场景
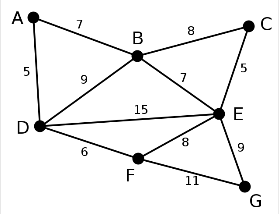
设想有9个村庄,这些村庄构成如下图所示的地理位置,每个村庄的直线距离都不一样。若要在每个村庄间架设网络线缆,若要保证成本最小,则需要选择一条能够联通9个村庄,且长度最小的路线
二. 最小生成树
-
最小生成树的概念
(1)一个带权值的图:网。所谓最小成本,就是用n-1条边把n个顶点连接起来,且连接起来的权值最小。
(2)我们把构造联通网的最小代价生成树称为最小生成树
(3)普里姆算法和克鲁斯卡尔算法 -
普里姆算法
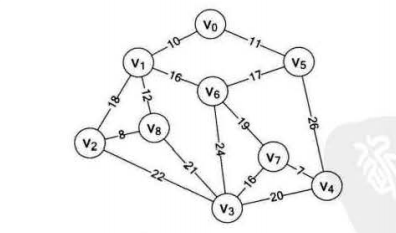
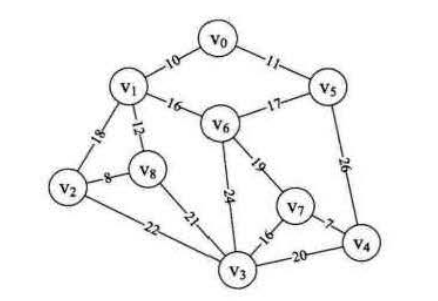
如下图,普利姆的最小生成树过程为:用Vs存储已经遍历的点,用Es存储已经遍历的边
(1)选择D为起点,加入Vs,与D连接的边中,权值最小的边为5,连接的点为A,因此将A加入到Vs,路径DA加入到Es。
(2)此时Vs中存在D和A。与DA连接的边中,权值最小的为6,连接的点为F,因此F加入到Vs,边DF加入到Es。
(3)此时Vs中存在DAF,与DAF连接的边中最小权值为7,连接的点为B,因此B加入Vs,路径AB加入Es
(4)重复以上过程,知道Vs中加入了所有的点#include <stdio.h> typedef char VertexType; typedef int EdgeType; #define MAXVEX 100 #define IUNFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表*/ EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵 */ int vnum,edgenum; /*定点的个数和边的个数*/ }MGraphy; /** * 普里母最小生成树:邻接表表示,时间复杂度为O(n方) * @param g */ void miniSpanTree_Prim(MGraphy *g){ int adjVetex[MAXVEX] = {0}; // 保存相关定点下标 int lowcost[MAXVEX]; // 保存相关顶点间的权值 lowcost[0] = 0; for (int i = 1; i < g->vnum; ++i) // 循环除下标为0外的全部结点 lowcost[i] = g->arc[0][i]; // 初始化lowcost数组,每一个元素的值为0点和给点边的权值 for (int i = 1; i < g->vnum; ++i) { // 循环除下标为0外的全部结点 int min = IUNFINITY; // 初始化最小权值为无穷 int j=1,k=0; while(j<g->vnum){ if(lowcost[j] != 0 && lowcost[j]<min){ // lowcost[j]为0表示当前点与其他点的权值数组 min = lowcost[j]; k = j; // k为遍历到的最小权值边连接的点 } j++; } printf("(%d,%d)",adjVetex[k],k); // 打印当前顶点边中权值最小的边 lowcost[k] = 0; for (int j = 1; j < g->vnum; ++j) { if(lowcost[j] != 0 && g->arc[k][j] < lowcost[j]){ lowcost[j] = g->arc[k][j]; // 将较小边的权值并入lowcast adjVetex[j] = k; } } } } -
克鲁斯卡尔算法
克鲁斯卡尔算法从边的集合中挑选权值最小的,加入到选择的边集合中。如果这条边,予以选择的边构成了回路,则舍弃这条边。
如下图所示,克鲁斯卡尔的方法为:
(1)选择权值最小为7的边V7-V4
(2)选择权值最小为8的边V2-V8
(3)选择权值最小为10的边V1-V0
(4)选择权值最小为11的边V0-V5
(5)选择全职最小为12的边V1-V8,但是发现V1和V8全部是已经访问的点,所以会构成回路,舍弃
(6)选择权值最小为16的边V1-V6
(7)选择权值最小为16的边V3-V7
(8)。。。。/* 科鲁斯卡尔最小生成树的边的结构体 */ typedef struct{ int begin; int end; int weight; }Edge; typedef char VertexType; typedef int EdgeType; #define MAXVEX 100 #define IUNFINITY 65535 typedef struct { VertexType vexs[MAXVEX]; /* 顶点表*/ EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵 */ int vnum,edgenum; /*定点的个数和边的个数*/ }MGraphy; /** * 查找连线顶点的尾部下标 */ int find(int *parement,int f){ while (parement[f] > 0) f= parement[f]; return f; } void miniSpan_Kruskal(MGraphy *g){ Edge edges[g->edgenum]; // 定义边集数组 int parement[g->vnum] = {0}; // 定义一个数组,用来判断是否形成回路 /** * 此处省略将邻接矩阵g转化为边集数组edges,并按照权值由大到小排序的过程 */ for(int i=0;i<g->edgenum;i++){ int n = find(parement,edges[i].begin); int m = find(parement,edges[i].end); if(n!=m){ // n != m说明没有形成环路 parement[n] = m; // 将此边的为节点放入到下标为起点的parement数组中 printf("(%d,%d) %d",edges[i].begin,edges[i].end,edges[i].weight); } } }
7.5 最短路径
一. 迪杰斯特拉
-
迪杰斯特拉算法
(1)迪杰斯特拉,计算的是一个点到其余所有点的最短路径。
(2)它的基本思想:
如果点 i 到点 j 的最短路径经过k,则ij路径中,i到k的那一段一定是i到k的最短路径。 -
查找方法:
(1)声明2个一维数组:一个用来标识当前顶点是否已经找到最短路径。另一个数组用来记录v0到该点的最短路径中,该点的前一个顶点是什么。
(2)比较:计算\(v_0\)到\(v_i\)的最短路径时,比较\(v_0\)\(v_i\)与\(v_0\)\(v_k\)+\(v_k\)\(v_i\)的大小,而\(v_0v_k\)与\(v_kv_i\)的值是暂时得出的记录在数组中的最短路径。 -
算法实现:基于邻接矩阵
#include "graphy/graphy.c" // 邻接矩阵 #define MAXVEX 9 #define INFINITY 65535 typedef int Pathmatrix[MAXVEX]; //存储最短路径下标的数组 typedef int ShortPathTable[MAXVEX]; //存储到各点最短路径的权值和 /** * 迪杰斯特拉:求有向图G的V[0]到其余各点的最短路径及带权长度 * @return */ void shortestPath_Dijkstra(MGraphy *g,int v0,Pathmatrix *p,ShortPathTable *sptable){ int final[MAXVEX] = {0}; *p = {0}; // 初始化最短路径数组为0 for (int i = 0; i < g->vnum; ++i) (*sptable)[i] = g->arc[v0][i]; //初始化sptable:让最短路径为图中v0和其余各顶点的权值 (*sptable)[v0] = 0; // sptable记录v0到v0的权值为0 final[v0] = 1; // final数组,记录以求得v0到v0的最短路径 /* 每次循环求得v0到顶点v的最短路径 */ for (int i = 0; i< g->vnum ; ++i) { int min = INFINITY; int k; for (int j = 0; j < g->vnum; ++j) { // 循环每个顶点 if(! final[j] && (*sptable)[j] < min){ k = j; // 这个k只是把j的作用域扩大出去,供后面计算a min = (*sptable)[j]; // 让min=当前被遍历顶点与v0点的边的权值 } final[k] = 1; for (int w = 0; w < g->vnum ; ++w) { int a = min+g->arc[k][w]; // 上面让k=j,所以a=(*sptable)[j] + g->arc[j][w]。也就是:比如计算a0到a2,就比较a0a1+a1a2 与邻接矩阵中的a0a2边的权值 if(! final[w] && a < (*sptable)[w]) { (*sptable)[w] = a; (*p)[w] = k; // 这个k就是:假设该等式角标与程序无关,计算 a[i][j] > a[i][k]+a[k][j],记录i到j的最短路径中,j前面的节点 } } } } }
二. 弗洛伊德算法
-
弗洛伊德与迪杰斯特拉的区别
(1)它们都是基于比较\(v_0\)\(v_i\)与\(v_0\)\(v_k\)+\(v_k\)\(v_i\)的大小的基本算法。
(2)弗洛伊德三次循环计算出了每个点个其他点的最短路径,迪杰斯特拉算法用2次循环计算出了一个点到其他各点的最短路径 。
(3)如果要计算出全部的点到其他点的最短路径,他们都是\(O(n^2)\)typedef int Pathmatrix_Floyd[MAXVEX][MAXVEX]; //存储最短路径下标的数组 typedef int ShortPathTable_Floyd[MAXVEX][MAXVEX]; //存储到各点最短路径的权值和 void shortPath_Floyd(MGraphy *g,Pathmatrix_Floyd *p,ShortPathTable_Floyd *D){ for (int i = 0; i < ; ++i) { for (int j = 0; j < g->vnum; ++j) { (*D)[i][j] = g -> arc[i][j]; (*p)[i][j] = j; } } for (int i = 0; i < g->vnum; ++i) { for (int j = 0; j < g->vnum; ++j) { for (int k = 0; k < g->vnum; ++k) { if((*D)[j][k] > (*D)[j][i]+(*D)[i][k]){ (*D)[j][k] = (*D)[j][i]+(*D)[i][k]; (*p)[j][k] = (*p)[j][i]; } } } } }
7.6 拓扑排序
一. 拓扑排序的概念
- 拓扑排序是对AOV网输出的一个序列
- AOV网(Active on Vertex Network):在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系。这样的图称为活动的网。
二. 拓扑排序的算法
-
步骤:
从AOV网中选择一个入度为0的顶点然后删除此顶点,并删除以此顶点为。重复此步骤,直到输出全部顶点或AOV网中不存在入度为0的顶点为止。 -
拓扑排序中顶点的数据结构:
(1)前面求最小生成树和最短路径时,都是使用邻接矩阵,但由于拓扑排序中,需要删除顶点,所以使用邻接表方便。
(2)因为拓扑排序中,需要删除入度为0的顶点,所以在原先的顶点数据结构中,加入入度域in。使顶点接都变为
![image_1auud954h1rbs1cm014lb16l83ip.png-3.1kB][23]#include <malloc.h> #define MAXVEX 100 typedef struct EdgeNode{ /* 边表 */ int adjvex; /* 顶点下标 */ int weight; /* 权值 */ struct EdgeNode *next; /* 边表中的下一节点 */ }EdgeNode; typedef struct VertexNode{ /* 定点表 */ int in; int data; EdgeNode *firstEdge; }VertexNode,AdjList[MAXVEX]; typedef struct{ AdjList adjList; int numVertexes,numEdges; }graphAdjList,* GraphAdjList; /** * 拓扑排序 * @param gl :链表 * @return :若GL无回路,则输出排序序列并返回1;若有回路则返回-1 */ int topologicalSort(GraphAdjList gl){ int *stack = (int *)malloc(gl->numVertexes * sizeof(int)); // stack用于存储入度为0的节点 int top = 0; // stack栈顶指针 int count; // 加入到栈中节点个数 for (int i = 0; i < gl->numVertexes; ++i) if(gl->adjList[i].in == 0) stack[++top] = i; while(top!=0){ int gettop = stack[top--]; printf("%d -> ",gl->adjList[gettop].data); count ++; for(EdgeNode *e=gl->adjList[gettop].firstEdge; e ; e=e->next){ int k = e->adjvex; // 顶点的下标 if( ! (-- gl->adjList[k].in)) // 将k号顶点入度减1 stack[++top] = k; // 如果发现入度为0,则把该顶点加入到栈中 } } int res = (count < gl->numVertexes) ? -1 : 1; // 如果最后遍历到的个数小于图的总定点数,则说明有环存在,返回-1 return res; }
7.7 关键路径
一. 概念
-
拓扑排序是解决一个工程能否顺序进行的问题,
-
当需要计算一个工程完成的最短时间,就需要用关键路径。
-
拓扑排序使用的是AOV网(定点表示活动)。关键路径使用AOE网(边表示活动)。AOV网只能表示活动之间的制约关系,而AOE网可以用变得权值表示活动的持续时间。所以AOE网是建立在活动之间制约关系没有矛盾的基础上,再来分析整个工程需要多少时间。
-
路径长度:路径上各个活动持续的时间之和
关键路径:从源点到汇点具有的最大长度的路径
关键活动:关键路径上的活动
二. 关键路径算法
-
关键路径算法中需要的变量:
(1)事件最早开始时间etv(earlist time of vertex):顶点\(v_k\)的最早发生时间
(2)事件最晚开始时间ltv(latest time of vertex) :顶点\(v_k\)的最晚发生时间,超过此时间,会延误整个工期
(3)活动最早开始时间(earlist time of edge):弧\(a_k\)的最早发生时间
(4)活动最晚开始时间(latest time of edge) :弧\(a_k\)的最晚发生时间,就是不推迟工期的最晚开始时间int *etv,*ltv; /* 事件最早,最晚发生时间 */ int *stack2; /* 用于存储拓扑排序的栈 */ int top2 = 0; /* stack2的栈顶指针 */ int topologicalSort2(GraphAdjList gl){ int *stack = (int *)malloc(gl->numVertexes * sizeof(int)); /* 建栈将入度为0的顶点入栈 */ int top = 0; for (int i = 0; i < gl->numVertexes; ++i) { if(0 == gl->adjList[i].in) stack[++top] = i; } etv = (int *)malloc(gl->numVertexes * sizeof(int)); /* 时间最早开时间数组 */ for (int i = 0; i < gl->numVertexes; ++i) /* 初始化最早开始时间数组全0 */ etv[i] = 0; int count = 0; stack2 = (int *)malloc(gl->numVertexes * sizeof(int)); while (top !=0 ){ int gettop = stack[top--]; count ++; stack2[++top2] = gettop; /* 将弹出的顶点序号压入拓扑排序的栈 */ for (EdgeNode *e = gl->adjList[gettop].firstEdge; e ; e = e->next) { int k = e->adjvex; if( !(-- gl->adjList[k].in) ) stack[++top] = k; if( (etv[gettop] + e->weight) > etv[k] ) /* 求各点事件最早发生时间值 */ etv[k] = etv[gettop] + e->weight; } } if(count < gl->numVertexes) return -1; else return 1; } void criticalPath(GraphAdjList gl){ topologicalSort2(gl); ltv = (int *) malloc (gl->numVertexes * sizeof(int)); /* 事件最晚发生时间 */ for (int i = 0; i < gl->numVertexes; ++i) ltv[i] = etv[gl->numVertexes -1]; /* 初始化ltv */ int k; while(top2 != 0){ int gettop = stack2[top2--]; for(EdgeNode *e=gl->adjList[gettop].firstEdge ; e ; e=e->next){ k = e->adjvex; if(ltv[k] - e->weight < ltv[gettop]) ltv[gettop] = ltv[k] - e->weight; } } for (int j = 0; j < gl->numVertexes; ++j) { for (EdgeNode *e = gl->adjList[j].firstEdge; e ; e = e->next) { k = e->adjvex; int ete = etv[j]; /* 活动最早发生时间 */ int lte = ltv[k] - e->weight; /* 活动最迟发生时间 */ if(ete == lte) printf("<v_%d , v_%d> length: %d",gl->adjList[j].data,gl->adjList[k].data,e->weight); } } }