BUAA-OO第一单元总结
面向对象设计构造第一单元总结
1. 单元介绍和整体认识
(1)单元介绍
本单元的主要目标是实现对表达式的化简(包括去多余括号和合并同类项等)。
训练目标:在实践中体会层次化设计的思想。
考察知识:
1. Java基础语法和基本容器使用
2. 理解形式化表述
3. 多种字符串解析方法
(2)整体认识
-
对于层次化设计思想的理解
层次化是当前很流行的设计思路。在进行一个项目的规划和设计时,从实际需要出发,对目标按照规模和功能进行分层,每层分别作为不同的模块,封装属性、实现互相独立的功能,再通过继承、实现等关系共同构成项目的整体。作为面向对象的高级语言,Java提供了一系列适用于层次化设计的设计工具和思路。
我认为层次化可分为两个角度:数据层次化和行为层次化。
数据层次化在本单元作业中主要体现在表达式如何进行储存和处理的问题上。由于数学表达式带有括号、且不同的运算符的优先级不同,所以自然构成了一个根据优先级进行分层的递归结构。而大部分同学采用的“表达式--项--因子”的三层结构,本质上也是根据运算符的优先级对表达式进行分层的结果;将表达式用优先级较低的“ + - ”符号分开,得到项;再将项用优先级较高的“ * ”分割,得到因子。而表达式因子的存在,就是“ ( ) ”运算符优先级最高的体现。“( )”在拥有最高优先级的同时,也将内外分割为两个互不作用的部分、分别进行优先级处理,这也使得括号内的部分在作为外部表达式的因子的同时,又具有与外部表达式相同的结构。这样的特点,为我们通过递归算法对其进行分层处理奠定了基础。
行为层次化是建立在上面提到的数据层次化的基础上的。在进行表达式的预处理和解析时,通过递归调用不同层次的数据的parse() 、toString() 等方法,对整个表达式进行处理。
2.基于度量分析和UML类图的程序结构分析
HW01
UML类图
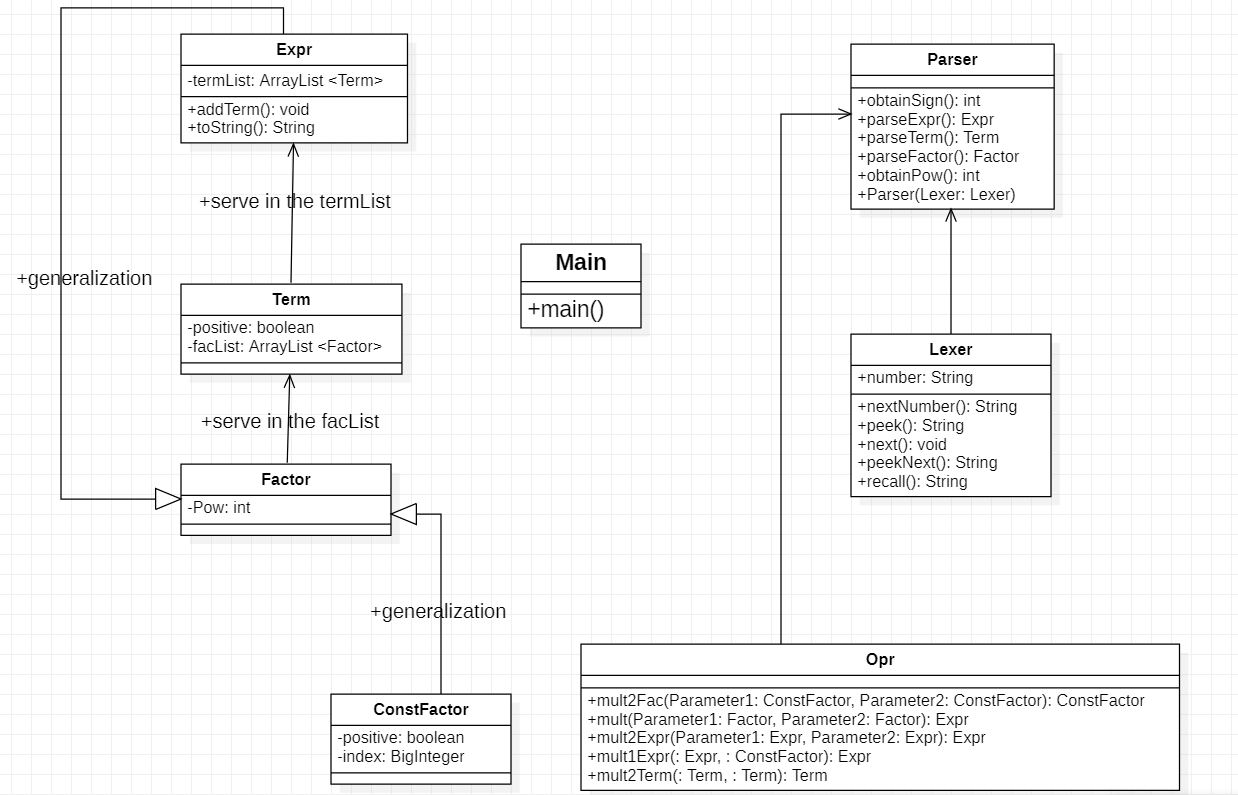
由于我在第二次和第三次作业中采用了另一种截然不同的处理方式,所以这种“lexer--parser”的设计思路并没有在后续作业中被延续下去。所以这里仅进行简要的分析。
这种设计方法通过lexer将表达式字符串分解成相互独立的元素,如因子、运算符号、括号等,再将之交由parser进行处理。另一个特点是本设计思路在处理字符串时并不是对整体进行统一处理,而是“读入一个element,处理一个element”,这是我第一次接触到这样的处理思路,也开拓了我在后续设计新的处理方法时的思路。
对于数据存储和处理,我将表达式按上面提到的 “优先级分层法” 分成因子、项、表达式三层,其中表达式又可以在加括号后作为因子出现,符合上面提到的递归处理特征。
度量分析
整体规模分析
| Class | total'Line | totalMethod |
|---|---|---|
| ConstFactor | 57 | 5 |
| Expr | 42 | 5 |
| Factor | 19 | 4 |
| Lexer | 79 | 7 |
| Main | 30 | 2 |
| Opr | 69 | 5 |
| Parser | 133 | 6 |
| Term | 109 | 8 |
| Total | 538 | 42 |
认知复杂度分析(已忽略认知复杂度低于5的数据)
| Method | CogC | ev | iv | v |
|---|---|---|---|---|
| Lexer.next() | 5.0 | 2.0 | 5.0 | 6.0 |
| Lexer.peekNext() | 5.0 | 2.0 | 4.0 | 6.0 |
| Opr.mult(Factor, Factor) | 5.0 | 4.0 | 4.0 | 5.0 |
| Parser.obtainSign() | 15.0 | 4.0 | 4.0 | 7.0 |
| Parser.parseFactor() | 11.0 | 3.0 | 5.0 | 6.0 |
| Term.toString() | 40.0 | 3.0 | 16.0 | 21.0 |
由图可知Term类重写的toString方法的认知复杂度明显高于其他各类的方法,这里单独列出方法设计的细节:
public String toString() { //大概思路就是先把整个term处理成一个没有括号的大表达式,然后带着符号输出(别忘了符号)
int numMin = 0;
for (Factor factor : facList) {
if (factor instanceof ConstFactor) { //把项中所有常数变量的符号统一提出来
if (!((ConstFactor) factor).isPositive()) {
numMin = numMin + 1;
}
}
else if (factor instanceof Expr) { //把所有带指数的表达式变量转化为不带指数的表达式变量
if (factor.getPow() != 1) {
factor = elimiPow((Expr) factor);
if (factor.getPow() == 0) {
factor = new ConstFactor();
((ConstFactor) factor).setIndex(BigInteger.ONE);
}
}
}
}
if (numMin % 2 == 1) {
this.positive = !this.positive;
}
//这里应该完成term中factor相乘的功能
//这时的factor应该已经没有带指数的表达式因子了
Factor temp = new Factor();
Factor prev = new Factor();
for (int i = 1; i < facList.size(); i = i + 1) {
temp = facList.get(i);
prev = facList.get(i - 1);
if (temp instanceof Expr | prev instanceof Expr) {
facList.set(i, Opr.mult(temp, prev));
}
else {
facList.set(i, Opr.mult2Fac((ConstFactor) temp,(ConstFactor) prev));
}
}
int size = facList.size();
for (int i = 0; i < size - 1; i = i + 1) {
facList.remove(0);
}
//到这里,facList中应该只剩下一个factor,也就是它的运算结果了
if (facList.get(0) instanceof Expr && facList.get(0).getPow() != 0) {
ArrayList<Term> termList = ((Expr) facList.get(0)).getTermList();
StringBuilder sb = new StringBuilder();
for (Term term : termList) {
if (!this.isPositive()) {
term.setPositive(!term.isPositive());
}
sb.append(term.isPositive() ? "+" : "-");
ArrayList<Factor> factorListHere = term.getFacList();
int i = 0;
sb.append(factorListHere.get(0).toString());
for (i = 1; i < factorListHere.size(); i = i + 1) {
sb.append("*");
sb.append(factorListHere.get(i).toString());
}
}
return sb.toString();
}
else if (facList.get(0) instanceof Expr && facList.get(0).getPow() == 0) {
return (this.isPositive() ? "+" : "-") + "1";
}
else {
return (this.isPositive() ? "+" : "-") + facList.get(0).toString();
}
}
我采用了parser部分只负责将数据解析,然后将去括号和优化的任务交给toString方法的设计思路。这样为toString方法增加了过多的负担,导致理解难度上升、简介程度下降,现在看来是一个并不特别合理的设计。
内聚耦合情况分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| ConstFactor | 1.2222222222222223 | 3.0 | 11.0 |
| Expr | 1.3333333333333333 | 3.0 | 8.0 |
| Factor | 1.0 | 1.0 | 4.0 |
| Lexer | 2.4285714285714284 | 5.0 | 17.0 |
| Main | 1.5 | 2.0 | 3.0 |
| Opr | 2.8 | 4.0 | 14.0 |
| Parser | 3.6666666666666665 | 7.0 | 22.0 |
| Term | 3.375 | 19.0 | 27.0 |
| Total | 106.0 | ||
| Average | 2.25531914893617 | 5.5 | 13.25 |
由上表可知,复杂度主要集中在Parser和Term上,说明在任务中主要进行文本处理的parser模块是最复杂的,而且文本处理和数据存储输出两部分的复杂度分别集中在Parser类和Term类,说明本次任务的内聚性较高。由上面的UML类图可知,程序的耦合程度较低,各个模块只通过比较简单的接口相互衔接,达到了“高内聚,低耦合”的设计目标。
hw02、hw03
因为我在第二、三次作业中采用了与第一次不同的处理方法,而第二、三次之间的衔接又比较紧密、进行的改动也较小,所以在这里共同讨论。
(0)整体概览
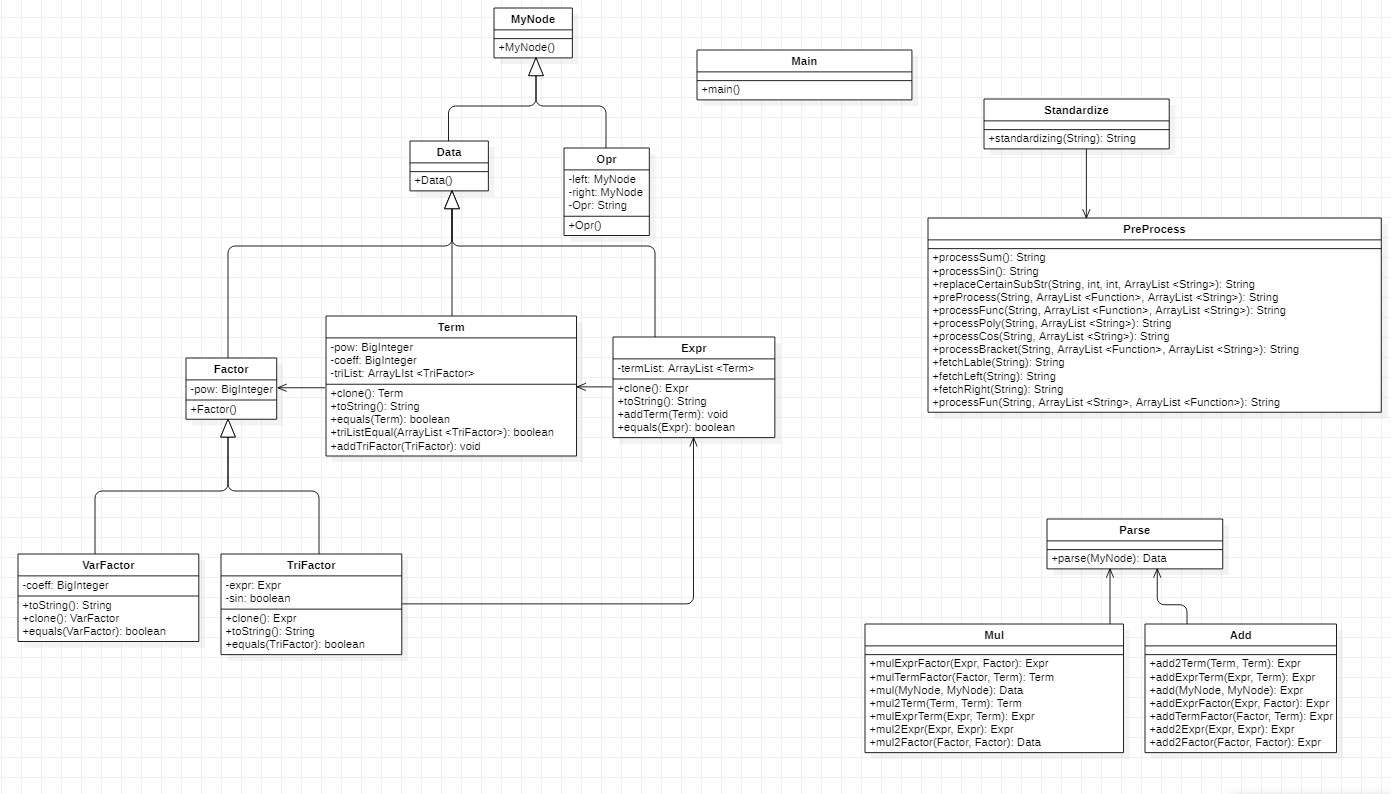
我的设计方式主要由预处理模块、解析模块、数据存储和输出模块三部分组成。在这里先对整体的思路进行介绍,下文将用单独的篇章分别介绍三个模块的具体实现。其中预处理模块借鉴了官方包的处理思路:将表达式拆分成多个运算符和操作数组成的标签;解析模块将预处理后得到的表达式树进行加减、乘法、指数运算;最终由输出模块化简并输出。
本设计思路如下:先由预处理模块中的 standardizing 方法将输入的自定义函数和表达式进行初步预处理,也就是去多余括号和多余正负号。经过这一步处理,我们就得到了符合数学规范的表达式。之后,再由PreProcess中的方法对表达式进行进一步预处理。这里,通过对表达式中的各个元素(因子、运算符、括号)的优先级进行排序,按这个顺序对表达式进行分层并替换。具体的实现方法是:由于优先级:括号(包括函数中的括号) > 指数符号 > * > [ + - ] ,先识别表达式中的括号并对其中的内容使用preProcess进行递归处理,将函数名替换为已经经过preProcess预处理的函数体对应的标签,将括号中的表达式使用preProcess进行替换,得到表达式对应的标签(标签由三部分组成,运算符和左右子节点,左右子节点分别又作为一个标签,拥有运算符和左右子节点,构成递归结构);
public class Opr extends MyNode {
private MyNode left;
private MyNode right;
private String opr;
public Opr(MyNode left, MyNode right, String opr) {
this.left = left;
this.right = right;
this.opr = opr;
}
}
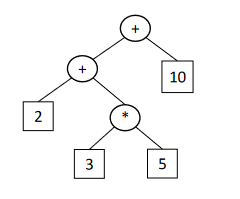
所有括号取出后,得到一个没有括号的表达式,原来作为括号出现的部分都转换为了标签、可以看作一个操作数;只有由preProcess中处理指数、乘号、加减号的部分按优先级一次处理,最终得到一个能够代表整个原表达式的标签。这样,我们就得到了一个原表达式的表达式树。
后续处理与HW01基本相同,将读入的表达式树进行运算,并转化为 “ 表达式 - 项 - 因子 ” 的三层递归结构,便于后续的合并和输出。
在 “ 项 ” 这一层次的设计中,我对原有的结构进行了改进。为了方便后续的化简和运算,我将项的所有常量因子和自变量因子、幂函数因子合并为由coefficience * x ** power表示,这样项就在此基础上增加一个三角函数的列表即可。这样,将存储多个不同种类因子转化为存储整体的系数和指数,方便了后续的计算、合并同类相、比较。
(1)预处理模块

度量分析
| Class | total'Line | totalMethod |
|---|---|---|
| PreProcess | 360 | 11 |
| Standardize | 42 | 1 |
| Total | 402 | 12 |
耦合内聚分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| preprocess.PreProcess | 5.416666666666667 | 10.0 | 65.0 |
| preprocess.Standardize | 7.0 | 7.0 | 7.0 |
| Total | 72.0 | ||
| Average | 5.538461538461538 | 8.5 | 36.0 |
(2)解析模块

度量分析
| Class | total'Line | totalMethod |
|---|---|---|
| Merge | 56 | 2 |
| Parse | 145 | 1 |
| Total | 201 | 3 |
耦合内聚分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| parse.Merge | 6.0 | 7.0 | 12.0 |
| parse.Parse | 22.0 | 22.0 | 22.0 |
| Total | 34.0 | ||
| Average | 11.333333333333334 | 14.5 | 17.0 |
(3)数据存储与输出
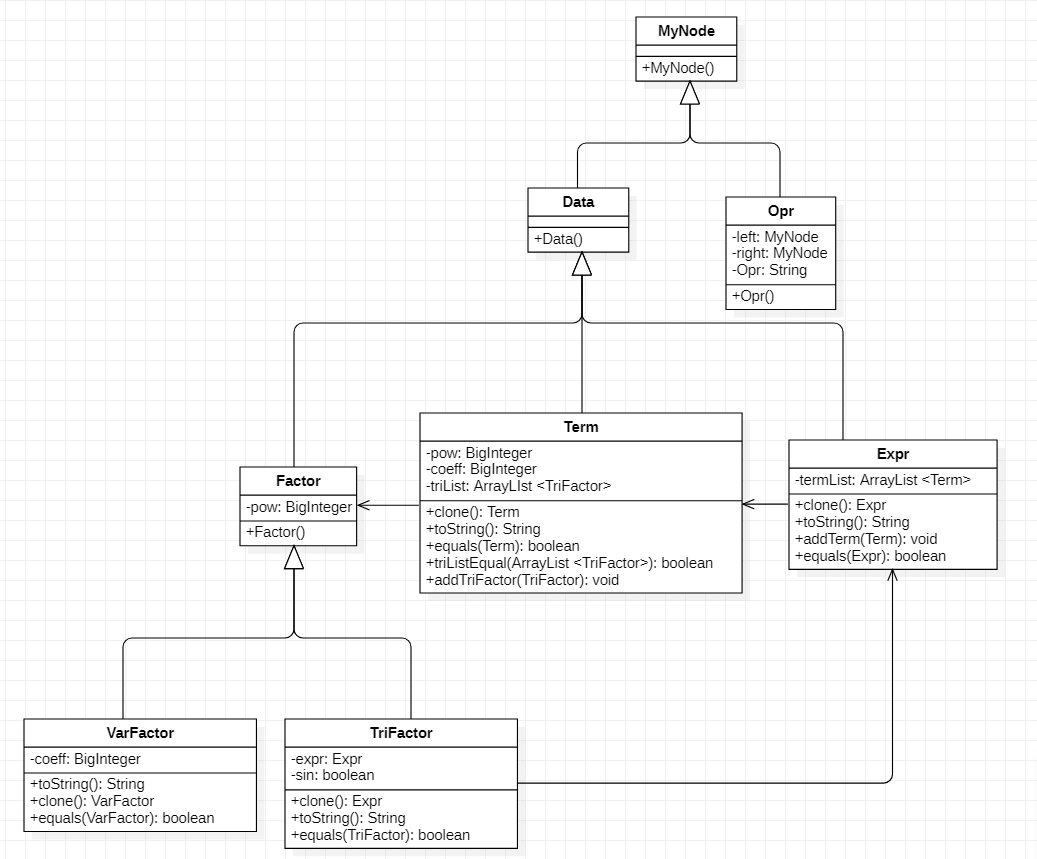
耦合内聚分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| datastructure.Data | 0.0 | ||
| datastructure.Expr | 2.8333333333333335 | 6.0 | 17.0 |
| datastructure.Factor | 1.0 | 1.0 | 2.0 |
| datastructure.Function | 1.6 | 6.0 | 16.0 |
| datastructure.MyNode | 0.0 | ||
| datastructure.Opr | 1.0 | 1.0 | 8.0 |
| datastructure.Term | 2.8181818181818183 | 11.0 | 31.0 |
| datastructure.TriFactor | 1.4285714285714286 | 3.0 | 10.0 |
| datastructure.VarFactor | 2.1666666666666665 | 7.0 | 13.0 |
| Total | 97.0 | ||
| Average | 1.94 | 5.0 | 10.777777777777779 |
根据类图和耦合内聚分析可知,本单元作业中主要问题在于preProcess模块的设计。因为将处理自定义函数、求和函数、普通表达式的功能集成到一个类中,虽然满足了内聚的要求,但多层递归的设计方法使代码比较臃肿、认知复杂度较高。
3.bug分析
(1)自己程序漏洞
第一次作业的主要问题在于 “浅拷贝” 和 “深拷贝” 没有加以区分导致的程序功能抽搐(出现了一些乍一看难以用科学解释的bug),为了解决这个问题,在后续作业中我先是重写了构造方法,后来又为所有数据结构类增加了 “clone” 方法,以空间换正确性。
第二次作业没有发现明显的bug。
第三次作业主要bug为sum求和函数没有考虑 start 和 end 存在BigInteger情况,由此被同房间几乎所有人hack了一遍;还有一个bug存在于Term类的toString中;三角函数括号中的表达式是使用Expr的toString来处理的,Expr的toString又递归调用了Term的toString方法;Term的toString方法判断了当系数为正和系数为负的情况,系数为0时直接返回0,但是当Expr中存在多个Term时,由于每个Term前的加减号是由Term的toString加入的,所以当同时存在0和非零的项时,就会缺少0项前的正负号,如1+0会被显示为10.这是一个比较隐蔽的逻辑漏洞。
至于出现bug和未出现bug的方法在复杂度上的差异,在我的设计中并没有明显的证据显示复杂度与bug出现率间存在明显相关(可能是因为在我自己测试的时候比较着重测试复杂度高的部分、反而忽视了简单的部分的原因吧~)。不过可以确定,复杂度越高,就会伴随着理解难度骤增、内聚程度降低。这样的复杂度对于后续调试和迭代都有很大压力。
(2)互测策略
本单元由于刚刚接触互测机制,主要是使用在自己设计过程中出现的bug测试别人的代码。之后的测试中,可以更加有针对性地对代码进行分析。根据任务的要求判断可能在迭代中出bug的模块,确定了可能的出错点后再仔细分析逻辑的错误。
4.优化分析
本单元任务的优化主要是如何判断相等并合并同类项,以及去掉值为0的三角函数和项。
由于我对项的结构进行了修改,所以这个任务比较方便完成;我Expr、Term和TriFactor三个类中增加了 equals() 方法,用于判断是否相等,作为合并同类项的判断依据如果判断得到两个term的pow、TriList部分都相同,则将coeff相加并合并,等等。至于降幂、和差化积等等高级操作我认为反而会牺牲过多的代码简洁性,并催生很多潜在的bug。
5.设计体验
架构的进化过程已经在前文介绍,就不在这里赘述了~
本单元的作业是我第一次自主完成的较大规模程序。这对于我和我的电脑来说都是一次挑战。 牢骚就不提了,要说感想的话,应该是第一单元没有把高内聚、低耦合做得很好,对java的理解也并不深刻、透彻,导致写出来了一个说起来算面向对象,但是逻辑更偏向于面向过程的东西(说实话,我感觉第一单元主要就是一个面向过程的任务,可能是我理解还不够深刻吧)。希望下次作业中不会再出现纯粹的方法类,能够更完美地把方法嵌入到相应的类中、和数据有更好的互动。
希望能够更好地安排时间,利用闲暇时间巩固java基础和内在原理,增进对各个方法的理解,减少因为知识理解有缺陷而产生的错误。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号